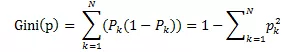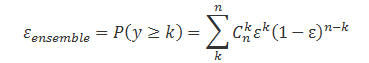随机森林算法介绍
原创: 傅佳 Refinitiv创新实验室ARGO 9月24日
专家审核:吴攀 石海龙 谭伟
审 核:陈超 施天璐 wk
"本篇包含少量基本数学公式,阅读需要约7分钟"
上次我们公众号发表了决策树算法的文章,这次基于决策树算法,我们进一步阐述其进阶算法--随机森林(RF),本文主要将五个方面阐述。
-
什么是随机森林
-
相关基本概念
-
算法介绍
-
sklearn库参数
-
知识扩展
一 什么是随机森林
为什么会出现随机森林,就要从决策树讲起。决策树优点很多,比如可解释性强,符合人类理解,运算速度快等。 但最大的缺点是,剪枝后也容易过拟合。2001年出现了随机森林算法,缓解了这一问题。
那什么是随机森林? 简而言之,就是随机生成一片由决策树构成的森林。
但随机森林的生成面临两个主要问题。 因为基于同样的数据,同样的特征,按照同样的决策树算法,只能建一颗树,同样的树复制上千万次没有意义,所以建立随机森林的第一个问题就是---怎么建立不同的树。其次,如果建立了不同的树组成的森林后,每个树都会得到自己的分类结果,如何从每棵树的各自决策下得到总体最终的结果呢? 这就是随机森林面临的第二个问题。
二 相关基本概念
在进入随机森林的讲解之前,我们先回顾一下决策树的一些核心概念。
a 信息量,信息熵,信息增益及基尼不纯度
1) 信息量
【概念】 信息多少的度量,它有如下特点
-
单调性,信息量和事件发生的概率有关,事件发生的概率越低,信息量越大。
-
非负性,信息量应该是非负的,必然发生的事件信息量为0。
-
累加性,两个事件的信息量可以相加,并且两个独立事件的联合信息量应该是它们各自信息量的和
【数学公式】
为什么用以二为底的对数,简单的理解,因为log函数能满足第2第3个条件,加上负号就满足了第一个条件,而用2为底是跟信息论里说的字节位数相关。
| 例如,德国队获的世界杯冠军,概率相对比较大,比如50%,则相应的信息量为 中国队获得世界杯冠军,因为中国队获取世界杯冠军的概率很低,比如0.1%,这个信息量则为 所以当它发生时,就会引发大家广泛讨论,去挖掘它产生的原因 |
2) 信息熵(Entropy)
【概念】用来度量随机变量的不确定性
【数学公式】
| 依旧以世界杯为例,德国 vs 巴西, 胜率比50% vs 50%, 则信息熵 中国队 vs 巴西, 胜率比 0.1% vs 99.9%, 则信息熵为 可以看出,当两队势均力敌时,不确定性越大,熵越大,而结果越确定,熵则越小,所以熵表明了信息的不确定性。 |
3) 信息增益
【概念】信息增益以某特征划分数据集前后的熵的差值。 划分前样本集合D的熵是一定的 ,为entropy(前),使用某个特征A划分数据集D,计算划分后的数据子集的熵 entropy(后)。信息增益越大,则这个特征的选择性越好,信息增益 = entropy(前) - entropy(后)
【数学公式】
g(D,A) = H(D)-H(D|A)
4) 基尼(gini)不纯度
【概念】表示在样本集合中一个随机选中的样本被分错的概率。基尼不纯度越小,则这个特征的选择性越好
【数学公式】
b 决策树的产生和分类
根据信息增益或基尼系数就可生成最优决策树,通俗地讲就是从众多特征中,先选出最能把数据划分更清楚的特征,切分后左右子树的样本尽可能的纯。之后在子树上以此种方式递归,生成了一棵决策树。
我们用的主要是三类决策树:ID3,C4.5和 CART树 (classification and regression tree)。其中,ID3和C4.5的计算和熵有关,CART树则用的是基尼不纯度。
随机森林更多用CART树,因为用基尼不纯度生成决策树比用信息增益计算工程效率更高一点。
三 算法介绍
回顾完第二部分基本概念,现在我们可以去思考本文开头提出的两个问题了。
怎么生成随机森林?
随机森林,其实是基于Bagging算法框架的一种实现。
那什么是Bagging? Bagging属于集成算法(Ensemble Learning)的一种,集成算法的核心思想是让机器学习的效果更好,单个不行,群殴走起。
Bagging的全称是Bootstrap aggregation,Bootstrap 来自成语’Pull up by your own bootstraps’,bootstraps本意是靴子后面的提手,这句话意思是依靠你自己的资源,解决问题。所以它被称为自助法,它是一种有放回的抽样方法。
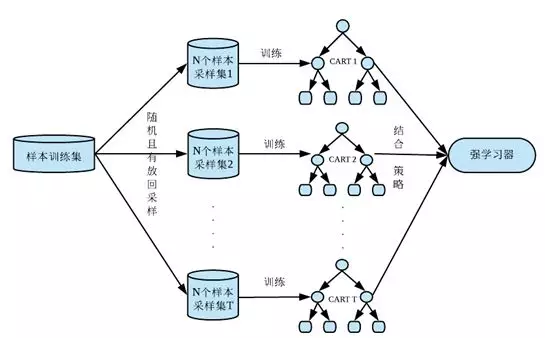
Bagging的每个弱学习器的训练集都是通过随机且有放回采样得到的,简略来说就是每次从原始样本中随机且有放回的采样N个训练样本,进行T轮采样,得到T个训练集,然后用这T个训练集,分别独立训练T个弱学习器,这T个弱学习器结合成一个强学习器,强学习器的结果作为整体的结果输出,如图所示:
随机森林就是用CART决策树作为Bagging算法中的弱学习器的实现,同时在每棵树的特征选择也用到了随机且有放回抽样,所以随机森林的生成规则如下:
1 从原始训练集中随机有放回采样N个训练样本,共进行T次采样,生成T个训练集
2 用T个训练集,分别训练T个CART树模型
3 如果特征维度为M,指定一个常数m < M,随机有放回从M个特征中选m个特征子集,根据这m个特征,生成CART树,分裂过程不剪枝
4 将生成的T棵决策树组成随机森林
5 对于分类问题,由T个CART树投票表决产生分类结果。对于回归问题,由T棵树预测结果的均值作为最终的预测结果
所以随机森林归的随机归纳为一句话,即数据随机采样,特征随机采样。
如何得到总体的分类结果?
投票表决有绝对多数投票法,相对多数投票法,加权投票法。均值有加权平均和简单平均,一般而言,在个体学习器性能相差较大时宜使用加权平均法,而在个体学习器性能相近时宜使用简单平均法。
Bagging 中还涉及到一个比较重要的概念:OOB(Out of Bag),意思是,通过统计,有放回的抽样,有一部分样本会多次出现,而另一部分样本不出现。Bagging每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集。对于这部分大约36.8%的没有被采样的数据,称为袋外数据OOB。这些数据没有参与模型的训练, 可以用来测试模型的泛化能力,所以随机森林可以不需要单独留出交叉验证的验证集。
注 : 对于自助法的抽样方法抽样时,为什么有接近36.8%不会被抽样? 是因为抽样红N次不被抽到的概率符合如下公式,当红N逼近于N,且N无穷大时,有
四 sklearn 库参数
随机森林的参数大部分和决策树一样,使用sklearn.tree.RandomForestClassfier类来实现随机森林算法,python调用如下:
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=10)
model.fit(train_X, train_y)
构造函数主要参数和意义如下:
model = RandomForestClassifier(n_estimators=10,criterion="gini",max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0,max_features="auto",max_leaf_nodes=None,min_impurity_decrease=0,min_impurity_split=None,bootstrap=True,oob_score=False, n_jobs=1, random_state=None,verbose=0,warm_start=False,class_weight=None)
[n_estimators]:string类型,可选(默认为10),森林里(决策)树的数目。就是弱学习器的最大迭代次数,或者说最大的弱学习器的个数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,计算量会太大,并且n_estimators到一定的数量后,再增大n_estimators获得的模型提升会很小,所以一般选择一个适中的数值,默认是10。
[criterion]:string类型,可选(默认为’gini’),即CART树做划分时对特征的评价标准。分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini, 另一个可选择的标准是信息增益。回归RF对应的CART回归树默认是均方差MSE,另一个可以选择的标准是绝对值MAE。一般来说选择默认的标准就已经很好了。
[max_features] : Int, float, string or None, 可选(默认为‘auto’), 随机森林里单个决策树的所使用的最多特征量。 显然,这个值越高,则随机森林的速度越慢。另外,该值越高,则虽仅森林中的多样性越低,同样会降低预测准确率。一般推荐这个值为总特征数量的均方根。
[max_depth] : Int or None,可选(默认为’None’) , 设置树的最大深度,默认为None,这样建树时,会使每一个叶节点只有一个类别,或是达到min_samples_split。数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。常用来解决过拟合。
[min_impurity_split] : Float类型。决策树在创建分支时,信息增益必须大于这个阀值,否则不分裂
[bootstrap] : 布尔型,可选(默认为‘True’),是否有放回的采样
[oob_score] : 布尔型,可选(默认为‘False’)。即是否采用袋外样本来评估模型的好坏。默认识False。推荐设置为True,因为袋外分数反应了一个模型拟合后的泛化能力。再加上OOB数据的存在,可以不需要交叉验证,所以可利用OOB Error作为评判m的指标。多单个模型的参数训练,我们知道可以用cross validation来进行,但是特别消耗时间,而且对于随机森林这种情况也没有大的必要,所以就用这个数据对决策树模型进行验证,算是一个简单的交叉验证。性能消耗小,但是效果不错。
[n_jobs] : interger类型,可选(默认为1)。用于拟合和预测并行运行的工作(作业)数量。这个在ensemble算法中非常重要,尤其是bagging(而非boosting,因为boosting的每次迭代之间有影响,所以很难进行并行化),因为可以并行从而提高性能。1=不并行;n:n个并行;-1:CPU有多少核,就启动多少job。
[random_state] : Int,RandomState instance or None(默认为’None’)。随机树生成器使用的种子,保证模型的输出具有可复制性。当它被赋于一个指定值,且模型训练具有相同的参数和相同的训练数据时,该模型将始终产生相同的结果。
[warm_start] : 布尔型,可选(默认为‘False’)。热启动,决定是否使用上次调用该类的结果,然后增加新的。
五 知识扩展
随机森林算法总结
到此为止,我们已经讲完了随机森林的算法,随机森林,就是“随机”和“森林”,这两点使它具有抗过拟合能力,使它更加精准,所以随机森林的优点如下:
1. 能处理高维数据,并且不用做特征选择
2. 模型泛化能力较强
3. 训练模型时速度快,成并行方式,即树之间相互独立
4. 有OOB,因此不需要单独划验证集
5. 模型训练结果准确度高
6. 有很强的抗干扰能力,所以当数据存在大量数据缺失,用随机森林是不错选择
但随机森林也不是万能的,它依旧也有缺点,比如
1. 给人感觉像黑盒子,几乎无法控制模型内部运行,只能在不同参数和随机种子之间进行尝试
2. 当数据噪声较大时,依旧会产生过拟合现象
但值得一提的是,Bagging方法只是集成方法的一种,将来我们还会提到Boosting方法,Boosting与决策树结合,也有很多非常出色的算法。
集成算法准确率分析
单个不行,群殴走起是否真的可行,集成算法的准确度一定比单个分类器更准吗?三个臭皮匠一定抵得过一个诸葛亮吗?我们可以简单的计算一下,以帮读者建立一个感性的认识。如果想深入了解,读者们可以看看霍夫汀不等式的证明。
如果每个分类器都具有相同的错误率ξ (预测错误),整个系统一共有n个成员分类器组成,且它们之间相互独立,基于少数服从多数投票原则,集成学习预测模型如果要出错,需要一半以上成员分类器预测错误,根据二项分布计算系统出错概率:
公式看来有点枯燥,举例说明。假设一共十一个弱分类器,分类器错误率分别为取0.49,0.50,0.51,即每个成员分类器的性能要优于随便猜、等于随便猜、差于随便猜时,我们集成分类器的错误率可以根据以上公式计算得到:
同时也用程序比较了成员分类器的错误率与集成系统错误率,得到集成系统的错误率会随着成员分类器错误率上升而上升,出错率0.5就是系统的出错率是否低于单个分类器的分界点,如图所示:
便可得知如果所有弱分类器错误率都在0.5以上,则集合效果也不会很好。而事实上,如果弱分类器错误率在0.5以上,我们会将输出结果反向,得到一个效果大于0.5的分类器。
本文随机森林就介绍到这了,欢迎大家留言提建议,并关注我们的公众号。
参考文档:
http://www.cnblogs.com/liuwu265/p/4690486.html
http://www.cnblogs.com/pinard/p/6131423.html
https://blog.csdn.net/sinat_29957455/article/details/79777187