机器学习实战笔记(一) K-近邻(k-NN)算法
本人也只是刚刚开始接触机器学习实战这本书，之前好多python的语法知识都有些模糊，所以注释写的比较详细，多谅解。
书中所用的代码用的是python2.x，但是现在python3的用的比较多，所以多出会对代码指出两者不同，这也是很多刚开始按照书上代码会报错的原因，都会在下面进行总结。
第一次写博客，内容好多地方自己可能也有理解错误的地方希望指出，里面的代码，文字，图片都是自己一点一点打出来，截出来的，希望支持，谢谢。
内容
1.算法简介......对KNN算法有一个具体的模型概念
2.代码实现......对机器学习实战书中约会网站实例的代码实现
3.算法扩展......参数选择及kd树
1.算法简介
在统计学习方法上是如此定义：给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例多数属于某个类，就把该输入实例归为这个类。是一种基本分类与回归方法。
输入：训练数据集T
输出：实例 x 所属的类 y
k-近邻算法的一般流程：
收集数据—>准备数据—>分析数据—>测试算法—>使用算法
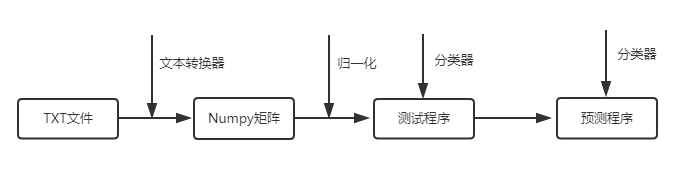
2.代码实现
代码实现书中给出了一种顺序，看完后其实可以按照算法简介中算法的一般流程列出这样一个顺序流程图：
机器学习实战是有附加的数据文件的，没有的话可以私信。有了数据，妈妈再也不用担心我的学习了。
实例：改进约会网站的配对效果
2.1 文本转换
因为机器学习实战附带的数据是txt文本，需要将其进行转换成NumPy中能处理的数组(矩阵)形式
文本转换器：将文本记录转换为NumPy的解析程序
def file2matrix(filename):
fr = open(filename)
arrayOnlines = fr.readlines()#readlines() 自动将文件内容分析成一个行的列表，该列表可以由 Python 的 for ... in ... 结构进行处理。
numberOflines = len(arrayOnlines)#得到文件行数
returnMat = zeros((numberOflines,3))#创建numpy矩阵
classLableVector = []#定义其为一个列表
index = 0
#解析文件数据到列表
for line in arrayOnlines:
line = line.strip()#根据()里的参数分割内容，默认是空格
listFromLine = line.split('\t')#返回分割后的字符串列表。
returnMat[index,:] = listFromLine[0:3]#将文件的内容矩阵化，并读取前三个内容
classLableVector.append(int(listFromLine[-1]))#读取最后一个内容，必须明确告诉解释器，列表中存储的元素为整形，否则会当作字符串进行处理
index += 1
return returnMat,classLableVector
测试时和预测时输入的是一个1*N的矩阵
标签Lables是一个M*1的矩阵
返回值中 returnMat是一个 m*3的矩阵，是数据样本的特征值 x classLableVector是数据样本按序号对应的所属的类y
这段代码中没有什么python2和3不同的地方，通过这个数据，可将数据文件转换成Numpy可处理的矩阵形式。
至此，完成了框图中第一步。
2.2归一化数值
打开数据文件 可以发现
每年获得的飞行常客里程数的影响远远大于其他两项，在处理这种不同范围的特征值时，我们通常采用的方法是将数值进行归一化。
下面的公式可将任意取值范围内的特征值转换为0到1区间：newValue = (oldValue - min) / (max - min)
归一化处理如下：
#归一化处理
def autoNorm(dataSet):#参数为输入的特征值矩阵
minVals = dataSet.min(0)#找出每一特征值的最小值
maxVals = dataSet.max(0)#找出每一特征值的最大值
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))#初始化尺寸归一化后的矩阵
m = dataSet.shape[0]#行数即样本个数
normDataSet = dataSet - tile(minVals, (m,1))#对应公式的 (oldValue - min)
normDataSet = normDataSet/tile(ranges, (m,1))#可直接相除，相当于每个元素除以对应元素
return normDataSet, ranges, minVals
引用百度资料：
发现是将a看作一个整体，进行(c,d)扩展为c行d列。（这里我是这么理解的，有误的话指出，谢谢哈）于是现在得到了三个数组： normDataSet 归一化后的训练集样本特征值数组 ranges 每个特征值对应的极差 minVals 每个特征值对应最小值 。
表面看来只有归一化的特征值数组有用，但其实深思在后面测试输入的样本时，还要对输入的预测样本进行归一化，这时候后面两者就要用上。
完成归一化，数据的处理算是基本完成了，按照流程图，下面进入编写分类器，来完成后续的测试程序和预测程序。
2.3分类器
利用KNN进行分类，先写出分类器的伪代码：
(1) 计算已知类别数据集中的点与当前点的之间距离
(2) 按照距离递增次序排序
(3) 选取与当前点距离最小的k个点
(4) 确定前k个点所在的类别的出现频率
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类根据伪代码写出代码：
def classify0(inX, dataSet, lables, k):#定义一个分类器
dataSetSize = dataSet.shape[0] #得到训练集样本的个数
diffMat = tile(inX, (dataSetSize,1)) - dataSet #将输入向量X进行扩展成训练集的行数，并减去训练集中的值 进行差值运算
#进行欧式距离的运算
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)#axis=1 是将矩阵或数组的行进行相加
distances = sqDistances ** 0.5
sortedDistIndicies = distances.argsort()
#argsort()按照一定的大小顺序进行排列 默认是按照升序进行排列
classCount = {}#字典类型
#对最近的k个训练集中的实例进行标签的计数工作
for i in range(k):
voteIlabel = lables[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)#按每个标签对应的数量升序进行排列
return sortedClassCount[0][0]#从k个标签数中最多的那个标签作为输入x的预估值在分类器这个程序中，有好多要注意的地方，自上而下来说：
(1).四个参数，前三个在前面也表述是三个矩阵，而参数k由定义知是选择的距离最近的k个点，机器学习实战选择了3，关于k的具体在第四部分在叙述。
(2).shape 函数 shape[0]返回的是行数，shape[1]返回的是列数，shape是返回行数列数的一个数组。
(3).argsort()函数 按照一定的大小顺序进行排列，默认是按照升序进行排列
(4).在倒数第二行的代码中，我第一次按照书中代码执行发现会报错 AttributeError: 'dict' object has no attribute 'iteritems' 然后发现代码没有问题，分析报错原因和iteritems这个迭代器有关，而且自己学python时不记得有用到这个(我学的书用的python3)，就觉得是不是python2和3的差，就去百度了下，发现又一个博客下写到：
Python 3.x里面，iteritems()和viewitems()这两个方法都已经删除，可用item()替代，于是我就尝试用items()替代，发现没有了错误，而且功能成功实现。
2.4测试程序
进行到流程图中的下一部分，编写测试程序。
def datingClassTest():
hoRitio = 0.1
datingDataMat, datingLabels = file2matrix('datingTestSet.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRitio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],\
datingLabels[numTestVecs:m],3)
print("the classifierResult came back with : %d, the real answer is: %d"\
%(classifierResult,datingLabels[i]))
if (classifierResult != datingLabels[i]):
errorCount +=1.0
print("the total error rate is: %f"%(errorCount/float(numTestVecs)))其中 hoRitio 是将得到的数据集分为训练集与测试集，在Ng的Machine Learning中他推荐的是3：7的分法，在这里是按1：9的分法。
首先将文件导入，刚开始导入datingTestSet时候，会报错，
错误是 ValueError: invalid literal for int() with base 10: 'largeDoses'，后来打开数据文件发现最后一列标签并非是数字，而是字符串，又发现还有一个txt，内容一模一样，只是最后的标签改为了数字，发现原来是导入错误了文件，改成另一个文件的文件名就没有错误了。
最后将测试程序执行完
5%的错误，可以接受。
2.5预测程序
预测程序和测试程序过程基本一致，要做的是要设置输入你要测试数据的特征值，并且对输入的特征值进行归一化，进行预测。
def classifyPerson():
resuleList = ['not at all', 'in a small doses', 'in large doses']#最后分类结果的所有可能
percentTats = float(input(\
"percentage of time spent playing video games?"))
ffMiles = float(input("frequent flier miles earned per year?"))
iceCream = float(input("liters of ice cream consumed per year?"))#输入三个特征值
datingDataMat,datingLables = file2matrix('datingTestSet.txt')#导入数据集及其对应的类别集
normMat, ranges, minVals = autoNorm(datingDataMat)#将输入的三个特征值进行归一化
inArr = array([ffMiles, percentTats, iceCream])
classifierResult = classify0((inArr-\
minVals)/ranges,normMat,datingLables,3)#利用分类器进行预测
print("You will probably like this person : ",\
resuleList[classifierResult - 1])#分类器得到的是一个数字，将数字转换成文字结果
最后，测试时输入
Enter后出来结果为：
测试结果出来了，程序完成！
3.算法扩展
我在学习机器学习实战前有幸读了李航老师的统计学习方法，里面有对k-近邻算法的更全面的内容，我挑了几个重要的地方记下来做成笔记。
在机器学习实战本章的最后内容里，有这样的叙述：使用这个算法时，效率并不高，因为算法要对每个测试向量做距离计算。k决策数就是k-近邻算法的优化版，可以节省大量的计算开销。
3.1kd树
关于kd树的介绍：
关于kd树的算法构造：
（均截自统计学习方法）
3.2参数k
现在再对参数K的选择，在统计学习方法有这样的叙述：
第一篇博客就写完了，文中或许有多处错误，希望指出共同学习。
希望里面的内容能有帮助！