【15-16年年末复习】递推复习

概述：

递推的题目，通常是可以由前一个或前几个状态推得当前的状态。递推中有三个要点：
①状态的表示
②递推方程
③初始值
同时要注意的还有循环的起始与结束条件
这其中比较困难的是第二步，求递推方程。确定好状态表示的是什么后，要确定如何才能推得这个状态，才能得到递推方程。当然，如果完全没有思路的时候也可以选择先找规律【当然正确率很低就是了
另外，同一道题可能有不同的状态表示以及不同的递推方程。

例1：

JDFZoj3004【超级楼梯】
Description
有一个超级楼梯共N级，刚开始时你在第一级，若每次只能跨上一级或两级，要走上第N级，共有多少种走法？
其中N（1 <= N <= 105）。

---

Input
输入一个整数N

---

Output
输出走到第N级的方案数，答案可能会很大，结果模上2333333。

---

第一步（状态的表示）：

该题目要求走到第n级的方案数，我们可以设状态f[i]为走到第i阶楼梯的方案数。

第二步（求递推方程）：

分析题目可知，当前楼梯可以从前一阶楼梯迈一步或者前两阶楼梯迈两步走到。所以递推方程就是

f[i] = f[i-1]+f[i-2];

第三步（确定初始值）：

因为一开始站在第一级台阶上，所以f[1] = 1,另外f[2]只能由f第一级跨一步走到，所以f[2] = 1。

代码如下

#include
int f[100005];
int mod = 2333333;
int main()
{
    int n;
    scanf("%d",&n);
    f[1] = 1;
    f[2] = 1;
    for(int i = 3;i<= n;i++)
    {
        f[i] = f[i-1]+f[i-2];
        f[i] = f[i]%mod;
    }
    printf("%d",f[n]);
    return 0;
}

tips：因为本题有mod所以注意不要爆数据范围。

例2：

JDFZoj3008【圆盘染色】
Description
将一个圆盘分为N (1 <= N <= 105)个扇形，每个扇形可涂红R、黄G、蓝B三种颜色中的一种，但相邻两个扇形的颜色必须不同，问有多少种涂法。

---

Input
输入一个整数N，表示将圆盘分为多少个扇区。

---

Output
输出一个整数，表示N个扇区染成RGB，相邻扇区颜色不同的方案数，答案可能会很大，结果模上2333333。

---

第一步（状态的表示）：

该题目要求n个扇区的圆盘染上3种颜色需要多少种方案，所以我们可以把f[i]作为有i个扇区时的方案。

第二步（求递推方程）：

首先，这是一个环，每个相邻的扇区颜色不能相同。我们可以把这个环从中间扯开，然后把它当做一个首尾颜色不能相同的串。

①已知我们f[i-1]中存储的方案都是合法的，即首尾的颜色不相同，此时第i个扇区只能填1种颜色，所以是f[i-1]。
但在我们要填第i个扇区的颜色时，之前有一些不合法的方案也可以合法了，这些不合法的方案即是填了i-1个扇区时首尾颜色相同的方案，共有f[i-2]种。此时第i个扇区可填的颜色为2种，即f[i-2]*2种。
再根据乘法原理可求得递推式：
f[i] = f[i-1]+2*f[i-2];

②我们可以先不考虑首尾相同的情况，那么填i个扇区时所有的方案数就是3 * 2 * 2 * …… * 2，即3乘上i-1个2。但是此时有一些不合法的方案，就是首尾相同的方案，为f[i-1]种，求得递推式为
f[i] = 3*2^(i-1)-f[i-1];

第三步（确定初始值）：

如果是第一种方法的话要初始化两个值f[1]与f[2]，填一个扇区的话有3种方案，两个扇区的话有6种方案。
f[1] = 3;f[2] = 6;
如果是第二种方法的话初始化一个值就够了，f[1] = 3;

第一种方法的代码如下

#include
int f[100005];
int mod = 2333333;
int main()
{
    int n;
    scanf("%d",&n);
    f[1] = 3;
    f[2] = 6;
    for(int i = 3;i<= n;i++)
    {
        f[i] = f[i-1]+2*f[i-2];
        f[i] = f[i]%mod;
    }
    printf("%d",f[n]);
    return 0;
}

tips：根据不同的递推式可能有不同的值需要特殊判断，要注意。

例3：

JDFZoj3013【毛毛虫】
Description
果园共用 N 棵苹果树，在第 S 棵树上有一条毛毛虫，这条毛毛虫每隔一分钟就会随机的爬到相邻的树上，不能原地不动。
假如毛毛虫在第2棵树上，下一分钟就可能在第1棵树上或第3棵树。
如果毛毛虫在第1棵树上，它下一分钟一定在第2棵树上。
问 M 分钟后，毛毛虫到达第 T 棵树的行走方案数？

---

Input
读入一行4个整数N S T M
1 < N <= 103
1 <= S,T <= N
0 < M <= 104

---

Output
输出一个整数，表示毛毛虫经过M分钟从S到达T的方案数，答案可能会很大，结果模上2333333。

---

第一步（状态的表示）：

该题目要求第m分钟到达树T的方案数，那么此时我们需要的数组就应该是二维f[i][j]的，用第一维表示第i分钟，用第二维表示此时到达了第j棵树。

第二步（求递推方程）：

如果第i秒到达第j棵树上，那么第i-1秒毛毛虫就在第j-1或者j+1棵树上，用加法原理可求得递推式
f[i][j] = f[i-1][j-1]+f[i-1][j+1];

第三步（确定初始值）：

题里已经说了，最开始的时候毛毛虫停在第s棵树上，所以f[0][s] = 1;

代码如下

#include
int f[10005][1005];
int mod = 2333333;
int main()
{
    int n,s,t,m;
    scanf("%d%d%d%d",&n,&s,&t,&m);
    f[0][s] = 1;
    for(int i = 1;i<= m;i++)
    {
        for(int j = 1;j<=n;j++)
        {
            f[i][j] = f[i-1][j-1]+f[i-1][j+1];
            f[i][j] = f[i][j]%mod;
        }
    }
    printf("%d",f[m][t]);
    return 0;
}

tips:这里要注意，如果毛毛虫想要走到第一棵或者最后一棵树上的话只能从第二棵树或者倒数第二棵树上走到，所以要注意循环的边界以及状态表示的边界
①可以特殊判断是否是第一棵树或者最后一棵树
②可以把左右边界开大，并赋初始值为零（这么写比较方便）

例4：

JDFZoj1180【弦】
Description
圆周上有N个点。连接任意多条（可能是0条）不相交的弦（共用端点也算相交）共有多少种方案？

---

Input
读入一个数N。1<=N<=1000。

---

Output
由于结果可能很大，你只需要输出这个答案mod 12345的值。

---

第一步（状态的表示）：

该题目要求的是圆上有n个点时连接弦的方案数，所以可以把状态表示为圆上有i个点时，方案数有f[i]种。

第二步（求递推方程）：

由题意可知，每两条弦都不相交，那么我每次在圆上连一条弦，都相当于把这个平面分成了两个部分，如图所示。

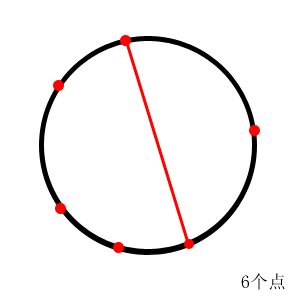
6个点在任意两点上连线，把原来的一个平面分为两个平面。相当于一个有3个点的圆和一个有一个点的圆。
此时根据乘法原理与加法原理就可以求出所有的方案数。
得到递推式为

第三步（确定初始值）：

圆上只有一个点时，方案数为f[1] = 1，即一条弦也不连。圆上有两个点时，可以连一条弦或者一个也不连，则方案书f[2] = 2。

代码如下

#include
int f[1001];
int main()
{
    int n;
    scanf("%d",&n);
    f[0] = 1;
    f[1] = 1;
    for(int i = 2;i<= n;i++)
    {
        f[i] = f[i-1];
        for(int j = 0;j<= i-2;j++)
        {
            f[i] = (f[i]+f[j]*f[i-2-j])%12345;
        }
    }
    printf("%d",f[n]);
    return 0;
}

tips：要注意循环的起始值与结束值