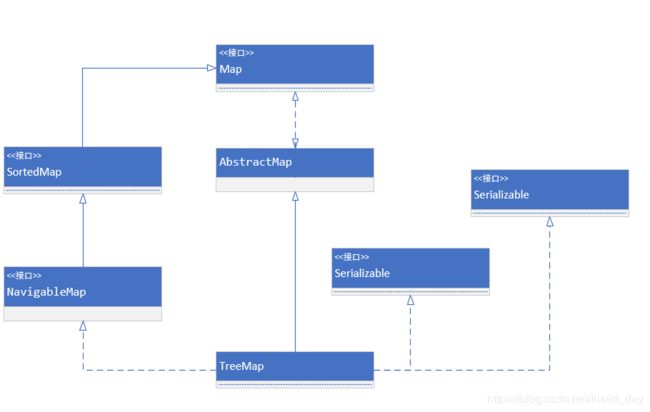
JDK 8 TreeMap 源码解析
【本文是为了梳理知识的总结性文章,总结了一些自认为相关的重要知识点,只为巩固记忆以及技术交流,忘批评指正。其中参考了很多前辈的文章,包括图片也是引用,如有冒犯,侵删。】
0 存储结构
TreeMap 是一个有序的Map,内部按照Key的排序结果来组织。一般如果没有需要排序的情况下,我们都使用HashMap或者多线程下使用ConcurrentHashMap,因为TreeMap的插入和删除的效率没有前两者高。但是如果需要有序的Map,那么就只能选TreeMap了,HashMap是基于Hash散列的,因此是无序的。从底层实现来看,TreeMap 是基于红黑树实现的,在学习之前需要先了解红黑树的基础知识,可以参考数据结构之红黑树Java实现。
1 类定义
public class TreeMap
extends AbstractMap
implements NavigableMap, Cloneable, java.io.Serializable 2 红黑树节点Entry结构
// 使用boolean值表示红黑树节点颜色
private static final boolean RED = false;
private static final boolean BLACK = true;
static final class Entry implements Map.Entry {
K key;
V value;
Entry left; // 左子树
Entry right; // 右子树
Entry parent; // 父节点
boolean color = BLACK; // 节点颜色
Entry(K key, V value, Entry parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
public K getKey() {
return key;
}
public V getValue() {
return value;
}
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
} 3 属性
/**
* 用于维护此TreeMap中顺序的比较器,如果它为null,则使用key的自然顺序。
*/
private final Comparator comparator;
// 树的根节点
private transient Entry root;
/**
* 树中节点的个数
*/
private transient int size = 0;
/**
* 树进行结构性修改的次数
*/
private transient int modCount = 0; 4 构造函数
主要用于初始化 comparator
// 默认使用自然排序,插入TreeMap的Key必须实现Comparable接口才能进行比较
public TreeMap() {
comparator = null;
}
// 使用指定的比较器,
public TreeMap(Comparator comparator) {
this.comparator = comparator;
}
// 基于现有的Map构造TreeMap
public TreeMap(Map m) {
comparator = null;
putAll(m);
}
// 构造一个和SortedMap具有相同顺序和元素的新Map
public TreeMap(SortedMap m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
} 5 常用方法
get(Object key)
public V get(Object key) {
// 调用getEntry方法进行查找
Entry p = getEntry(key);
// 不存在返回null
return (p==null ? null : p.value);
} getEntry方法,无论是基于自定义比较器的查找,还是基于自然排序比较器的比较,都是在二叉树下的查找。当前元素大于目标元素,向左找;当前元素小于目标元素,向右找。
final Entry getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
// 基于指定比较器的比较
return getEntryUsingComparator(key);
/* 自然排序比较 */
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
Entry p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0) // 当前元素大于目标元素,向左找
p = p.left;
else if (cmp > 0) // 当前元素小于目标元素,向右找
p = p.right;
else
return p;
}
return null;
}
final Entry getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator cpr = comparator;
if (cpr != null) {
Entry p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0) // 当前元素大于目标元素,向左找
p = p.left;
else if (cmp > 0) // 当前元素小于目标元素,向右找
p = p.right;
else
return p;
}
}
return null;
} put(K key,V value)
插入时先进行查找,看是否存在相同key的节点,存在就直接替换value,不存的话能找到要插入的位置parent, 构造新节点进行插入,然后调用fixAfterInsertion方法进行插入修复,插入修复设计红黑树的重新着色和旋转,详情见数据结构之红黑树Java实现。
public V put(K key, V value) {
// 根节点为空的情况
Entry t = root;
if (t == null) {
compare(key, key); // 类型检查,有可能为null
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
// split comparator and comparable paths
Comparator cpr = comparator;
if (cpr != null) {
// 使用自定义比较器进行查找
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value); // 存在重复的key,直接覆盖,返回旧值
} while (t != null);
}
else {
// 使用自然排序比较器进行查找
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value); // 存在重复的key,直接覆盖,返回旧值
} while (t != null);
}
// 不存在具有相同Key的节点,新建节点进行插入
Entry e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e; // 插入左侧
else
parent.right = e; // 插入右侧
fixAfterInsertion(e); // 插入修复
size++;
modCount++;
return null;
} remove(Object key)
public V remove(Object key) {
// 先找到目标节点
Entry p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
// 调用deleteEntry进行删除
deleteEntry(p);
return oldValue;
} deleteEntry删除方法, 删除过程,可以简单分为4种情况:
- 只有一个节点的情况;
- 删除点p的左右子树都为空;
- 只有一棵子树非空;
- 删除点p的左右子树都非空。
对于情况1,直接将根节点root置为null就可以;
对于情况2,直接将p删除,将p的parent指向p的指针置为null;
对于情况3,用非空子树替代p;
对于情况4,可以用p的后继s(树中大于p的最小的那个元素)代替p,然后删除后继s。后继s一定不是左右子树非空,就可以使用情况1、2、3进行处理。
删除修复方法fixAfterDeletion详见,数据结构之红黑树Java实现。
private void deleteEntry(Entry p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
// 删除节点p的左右子树都非空,将P 指向后继元素
if (p.left != null && p.right != null) {
Entry s = successor(p); // 寻找后继
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
// 删除点p只有一棵子树非空,从子树中选出替代元素
Entry replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
// 替换parent指向
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
// 删除P节点
p.left = p.right = p.parent = null;
// Fix replacement
// 插入修复
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // 只有一个节点p的情况
root = null;
} else { // 删除点p的左右子树都为空
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
} successor(Entry t)
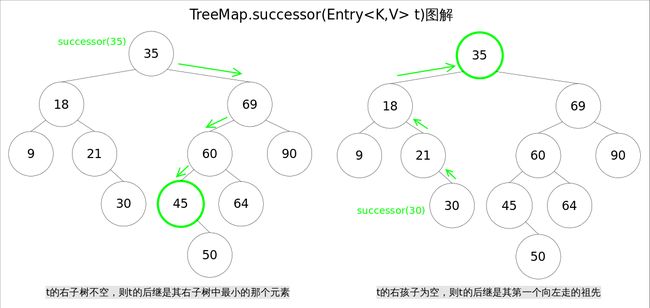
寻找后继的方法,对于一棵二叉查找树,给定节点t,其后继(树中比大于t的最小的那个元素)可以通过如下方式找到:
- t 的右子树不空,则t的后继是其右子树中最小的那个元素。
- t 的右孩子为空,则t的后继是其第一个向左走的祖先。
// 寻找节点后继函数successor()
static TreeMap.Entry successor(Entry t) {
if (t == null)
return null;
else if (t.right != null) {// t的右子树不空,则t的后继是其右子树中最小的那个元素
Entry p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {// t的右孩子为空,则t的后继是其第一个向左走的祖先
Entry p = t.parent;
Entry ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
} firstEntry()
寻找第一个节点,根据二叉查找树的性质,树的最做左边的节点最小。
public Map.Entry firstEntry() {
return exportEntry(getFirstEntry());
}
// 树的最左边的是最小值
final Entry getFirstEntry() {
Entry p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
// 返回简单不可变entry,如果为null,则返回null
static Map.Entry exportEntry(TreeMap.Entry e) {
return (e == null) ? null :
new AbstractMap.SimpleImmutableEntry<>(e);
} lastEntry()
返回树的最大的元素,根据二叉查找树的性质,树的最做右边的节点最小。
public Map.Entry lastEntry() {
return exportEntry(getLastEntry());
}
// 找到根节点的最右边节点
final Entry getLastEntry() {
Entry p = root;
if (p != null)
while (p.right != null)
p = p.right;
return p;
} lowerEntry(K key)
找到刚好小于Key的节点。
public Map.Entry lowerEntry(K key) {
return exportEntry(getLowerEntry(key));
}
final Entry getLowerEntry(K key) {
Entry p = root;
while (p != null) {
int cmp = compare(key, p.key);
if (cmp > 0) {
// key 比当前p.key大
if (p.right != null)
p = p.right; // 向右查找
else
// 比最大的右加点还大,返回最大值
return p;
} else {
// key 比当前p.key大
if (p.left != null) {
p = p.left;// 向左查找
} else {
// 比最低的左节点大,向上查找第一个左拐的父节点
Entry parent = p.parent;
Entry ch = p;
while (parent != null && ch == parent.left) {
ch = parent;
parent = parent.parent;
}
return parent;
}
}
}
return null;
} higherEntry(K key)
public Map.Entry higherEntry(K key) {
return exportEntry(getHigherEntry(key));
}
final Entry getHigherEntry(K key) {
Entry p = root;
while (p != null) {
int cmp = compare(key, p.key);
if (cmp < 0) {
// key 比当前p.key小
if (p.left != null)
p = p.left; // 向左查找
else
return p; // 比最小的左加点还小,返回最小值
} else {
// key 比当前p.key大
if (p.right != null) {
p = p.right; // 向右查找
} else {
// 比最低的右节点大,向上查找第一个右拐的父节点
Entry parent = p.parent;
Entry ch = p;
while (parent != null && ch == parent.right) {
ch = parent;
parent = parent.parent;
}
return parent;
}
}
}
return null;
} ......