Adversary Attack(对抗攻击)论文阅读笔记

引言:
最近开始学习Adversary Attack(对抗攻击)有关的内容，于是便从Ian GoodFollow的论文开始读起，后面每篇博客都会列举三篇的阅读笔记，来记录学习的经历。如果有讲得不到位或者您有什么想要补充的话，欢迎留言哦~

---

接下里将列举3篇论文：

1. Explaining and Harnessing Adversarial Examples(ICLR2015)
2. Adversarial machine learning at scale(ICLR2017)
3. ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD(ICLR2017)

不过这三篇论文基本讲述的内容都是差不多的。

---

1. Explaining and Harnessing Adversarial Examples(ICLR2015)

本文主要探究的是对抗样本攻击原理的探究以及利用对抗思想进行训练

针对对抗样本，其往往是在原输入$x$往其梯度方向进行扰动$\eta$所达到的
$$\tilde{x}=x+\eta$$

虽然只是对$x$进行了细微改动，但当进行计算后，会有

$$W^T\tilde{x}=W^{T}x+W^T\eta$$
一旦$x$的维度边高，$\eta$维度也会随之线性增加，由此即使是微不足道的改动(即$||\eta |{|}_{\infty }<ϵ$)，在进行$W^T\eta$计算操作后，也会有比较大的结果，因此会影响模型的预测结果。

作者还发现了一种相比于dropout更有效的正则化方法:

$$\tilde{J}(\theta ,x,y)=\alpha J(\theta ,x,y)+(1-\alpha )J(\theta ,x+ϵsign({▽}_{x}J(\theta ,x,y),y)$$
其中$x+ϵsign({▽}_{x}J(\theta ,x,y)$即为对抗样本。

此外作者还发现即使是low capacity的模型如shallow RBF network
$$p(y=1|x)=exp((x-\mu {)}^T\beta (x-\mu ))$$
对adversary sample有免疫效果。其原因是针对一个分类模型，其预测结果是根据与$\mu$的距离来确定的，在距离$\mu$较远的地方，则不是本类或者置信度低。

另外作者指出，一个adversary sample在不同的模型上，其预测错误的类别基本一致，这就暴露出现有的模型存在的缺陷。

Summarys:

1. 对抗性的例子可以解释为高维点积的一个性质。
   它们是模型过于线性的结果，而不是过于非线性的结果。
2. 由于对抗性扰动与模型的权向量高度一致，并且不同的模型在训练执行相同任务时学习相似的函数，因此可以解释不同模型间对抗性示例的泛化
3. 证明对抗性训练可以进行正规化;甚至比dropout更有效。
4. 易于优化的模型更容易受到对抗样本的影响。
5. 线性模型缺乏抵抗对抗性扰动的能力;只有具有隐藏层的结构(where the universal approximator theorem applies)才应该被训练来抵抗对抗性扰动。
6. 通过对输入分布进行训练的模型无法抵抗对抗样本。
7. 集成学习也无法有效抵抗对抗样本。

---

2. Adversarial machine learning at scale(ICLR2017)

本文主要介绍生成对抗样本的方法和对抗训练的方法

FGSM:

$$X^{adv}=x+ϵsign({▽}_{X}J(X,y_{true}))$$
该方法的优点：易实施且计算高效

    缺点：攻击成功率低

one-step target class methods:

$$X^{adv}=x-ϵsign({▽}_{X}J(X,y_{target}))$$
其中$y_{target}=argmi{n}_{y}p(y|X)$即偏离最远的错误类。

Basic iterative method:

$$X_0^{adv}=X,X_{N+1}^{adv}=Cli{p}_{X,ϵ}(X_N^{adv}+\alpha sign({▽}_{X}J(X_N^{adv},y_{true}))$$
其中$Cli{p}_{x,ϵ}(A)$denots element-wise clipping A, with $A_{i,j}$clipped to the $range[X_{i,j}-ϵ,X_{i,j}+ϵ]$

Iterative least-likely class method:
$$X_0^{adv}=X,X_{N+1}^{adv}=Cli{p}_{X,ϵ}(X_N^{adv}-\alpha sign({▽}_{X}J(X_N^{adv},y_{target}))$$
迭代方式是one-Step的"升级版"

疑惑点:总感觉迭代的$Cli{p}_{x,ϵ}(A)$不是论文中所写的 with $A_{i,j}$clipped to the $range[X_{i,j}-ϵ,X_{i,j}+ϵ]$

采用的损失函数为

$$Loss=\frac{1}{(m-k)+\lambda k}(\sum _{i\in CLEAN}L(X_i|y_i)+\lambda \sum _{i\in ADV}L(X_i^{adv}|y_i))$$
算法为

并且采用的是delaying adversarial training即前N轮只用clean数据进行训练，后面再采用clean和adversary样本共同训练。

Label Leaking:

其现象为model可以正确分类通过$y_{true}$产生的adversary sample但不能正确分类通过$y_{target}$产生的adversary sample。其表达的实验结果为:

其中Step 1.1表示Iterative least-likely class method。从中可以看出，出现Lable Leaking后这些one-step算法在有adversary images上准确率反而会提高。作者给出的解释为one-step算法通过$y_{true}$所使用的变换简单以至于被网络给学习到了，所以才会出现这种结果。因此作者建议，FGSM或者其他方式不要通过$y_{true}$产生adversary sample，建议不要直接接触$y_{true}$，因此$y_{target}$是一个比较好的备选。

transfer rate:

采用iterate方式建立的adversary sample在不同的模型上的attack效果不及one-step

其中transfer rate表示在source model上成功attack的adversary sample与在target model上成功的sample数目之比。所以要想攻击一个黑盒模型，最佳的攻击样本建议为one-step建立的样本。

---

3. ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD(ICLR2017)

文章大体上与上述两篇文章一致，只是多了一些拓展说明。

对比3种不同的攻击方法，我们可以得出以下结论：

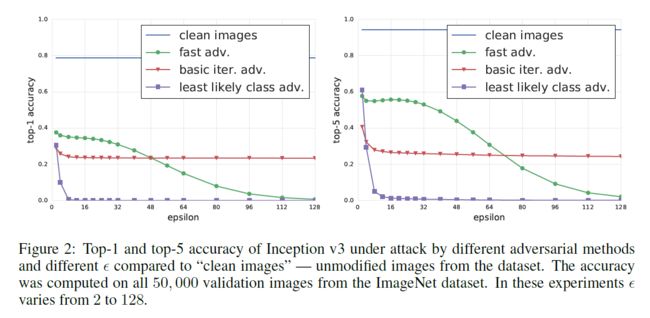
1. basic iter方式提高$ϵ$带来的收益不大，且当$ϵ$超过一定阈值后，继续提高不会带来明显作用
2. least likely class方式能够在$ϵ$比较小的情况下就能达到有效的攻击结果
3. fast方式会随着$ϵ$的增加而逐渐提高攻击性能，但相比与least likely class方式而言，其提高性能的根本原因是在于破坏了原始图片的大部分信息，如下图.

Photo Transform:

突发奇想地提出了一种叫做Photo Tranform的黑盒变换，其实其变换的本质只是将origin image打印出来，作为一种transform。

左边两幅图中，每张图都有两列，因为这个尺寸可能看不太清，故此说明一下：左边一列是origin image，右边一列是进行扰动后的adversary image。

首先考虑不加任何人为选择的随机采样结果

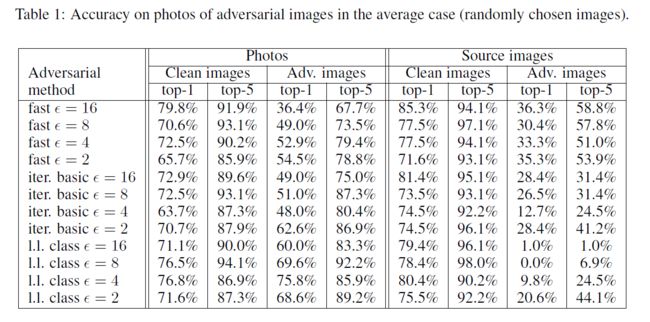
[Note]:这个table看起来有点难懂，按我自己的理解在，左边的$ϵ$针对的是Adv. images而Clean images是没有受到扰动的。

从table中可以看出，观察Adv. images对应的那2列(Photos和Source images),使用fast方法产生的Adv. images在进行Photo Transform时，准确率变化不明显，而其他iter方法产生的结果则差异较大，可以发现，当进行Photo Transform后，其准确率反而提升了。这里作者给出的解释为：基于iter的方法进行的扰动比较细微，而Photo Transform把这些细微的扰动给抵消了。因此就出现了准确率反而提高的结果。

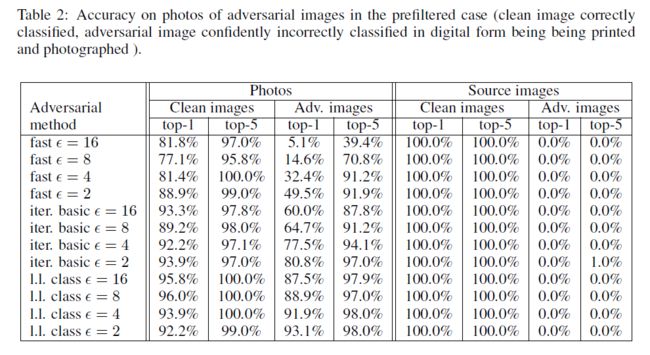
然后考虑人为选择的采样结果:(即在Clean image上正确分类，在Adversary image上错误分类的那些图片作为采样结果。)

可以看出，结果与预期一致，原因同上。

---

如果觉得我有地方讲的不好的或者有错误的欢迎给我留言，谢谢大家阅读（点个赞我可是会很开心的哦）~