“梯度下降法”理解

在学习神经网络的时候，反向传播，通常会用到梯度下降法去更新权值使得在不断迭代的过程中使得每层网络权值不断调整直到损失函数落入最小值（局部或全局）。

梯度下降法的基本公式是：

w:=w−η▽E

其中 E 为损失函数， η 为步长，下面解释上式如何理解，需要从方向导数开始讲起。

方向导数

偏导数反映的是函数研坐标轴方向的变化率，但仅考虑函数沿坐标轴方向但变化率是不够的。例如热空气要向冷空气的地方流动，气象学中就要确定大气温度、气压沿着某些方向的变化率。因此我们有必要来讨论函数沿任一指定方向的变化率问题。

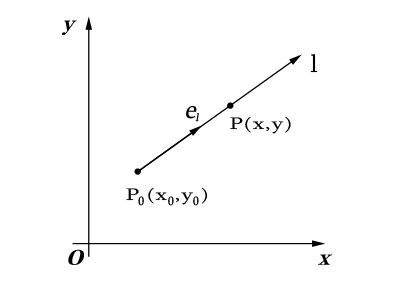
如下图， l 是 xOy 平面上过 P0 点的直线， el→ 为与直线 l 同方向的单位向量， el→=(cosα,cosβ)

则射线 l 的参数方程为：

{x=x0+tcosα，y=y0+tcosβ (t≥0)

则定义：
当 P 沿 l 趋于 P0 （即 t→0+ ）时的极限存在，那么称此极限为函数 f(x,y) 在点 P0 沿方向 l 的方向导数，记作 ∂f∂l|(x0,y0) ，即

∂f∂l|(x0,y0)=limt→0+f(x0+tcosα,y0+tcosβ)−f(x0,y0)t

故可知方向导数就是函数 f(x,y) 在点 P(x0,y0) 处沿方向 l 的变化率。

且存在定理：
如果函数 f(x,y) 在点 P0(x0,y0) 可微分，那么函数在该点沿任一方向 l 的方向倒数存在，且有

∂f∂l|(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ

其中 cosα 和 cosβ 是方向 l 的方向余弦。

梯度

在二元函数的情形，设函数 f(x,y) 在平面区域D内具有一阶连续偏导数，则对于每一点 P0(x0,y0)∈D ，都可定出一个向量

fx(x0,y0)i⃗ +fy(x0,y0)j⃗ 

这个向量称为函数 f(x,y) 在点 P0(x0,y0) 的梯度，记作 grad→f(x0,y0) 或 ▽f(x0,y0)=fx(x0,y0)i⃗ +fy(x0,y0)j⃗ 

若函数 f(x,y) 在点 P0(x0,y0) 可微，且 el→=(cosα,cosβ) 是与方向 l 同向的单位向量，那么

∂f∂l|(x0,y0)====fx(x0,y0)cosα+fy(x0,y0)cosβ▽f(x0,y0)⋅el→|▽f(x0,y0)|⋅1⋅cosθ|▽f(x0,y0)|cosθ

其中 θ=<▽f(x0,y0),el→> 。

由方向导数就是函数 f(x,y) 在点 P0(x0,y0) 处沿方向 l 的变化率：

[ 1 ] 若要求在点 P0(x0,y0) 趋于最大值最快方向（若比喻成上山，即找到最陡的一条上坡路，使得上山速度最快），则要使 ∂f∂l|(x0,y0) 取正最大值，即要： cosθ=1⇒θ=0 ，即 ∂f∂l|(x0,y0) 与 el→ 方向相同，此时

∂f∂l|(x0,y0)=|▽f(x0,y0)|

[ 2 ] 若要求在点 P0(x0,y0) 趋于最小值最快方向（若比喻成下山，即找到最陡的一条下坡路，使得下山速度最快），则要使 ∂f∂l|(x0,y0) 取负最大值，即要： cosθ=−1⇒θ=π ，即 ∂f∂l|(x0,y0) 与 el→ 方向相反，此时

∂f∂l|(x0,y0)=−|▽f(x0,y0)|

[ 3 ] 同理，若要求在点 P0(x0,y0) 移动最慢方向（不动），则要使 ∂f∂l|(x0,y0) 取最小值，即要： cosθ=0⇒θ=π2 ，即 ∂f∂l|(x0,y0) 与 el→ 方向垂直，此时

∂f∂l|(x0,y0)=0

根据上述可说明

w:==w−η▽Ew+η(−▽E)

为最快迭代到极小值点的参数更新方式。

（以上为本人理解，如有错误望诸位读者指教！）

参考：
《高等数学 第七版下册》同济大学数学系编