漫谈支持向量机（support vector machines，SVM ）

第一部分、概述

支持向量机（support vector machines，SVM）

• 一种二分类分类模型。
• 基本模型：定义在特征空间上的间隔最大的线性分类器
• 学习算法：求解凸二次规划的最优算法。
• 学习策略：间隔最大化，可形式化为一个求解凸二次规划（convex quadratic programming）的问题，也等价于正则化的合页损失函数的最小化问题。

支持向量机的方法

线性可分支持向量机（linear support vector machine in linearly）
当训练数据线性可分时，通过硬间隔最大化（hard margin maximization），学习一个线性的分类器，又称硬间隔支持向量机

线性支持向量机（linear support vector machine）
当训练数据近似线性可分时，通过软间隔最大化（soft margin maximization），学习一个线性的分类器，即线性支持向量 机，又称软间隔支持向量机

非线性支持向量机（non-linear support vector machine）
当训练数据线性不可分时，通过核技巧（kernel trick）及软间隔最大化，学习非线性支持向量机。

---

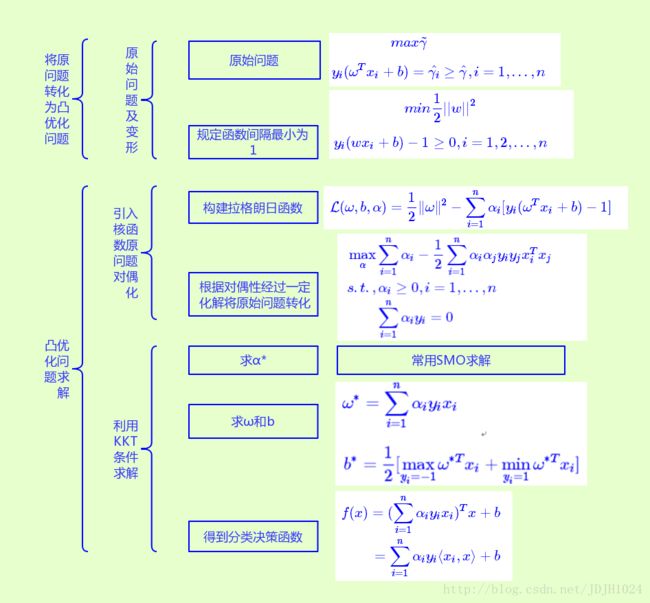
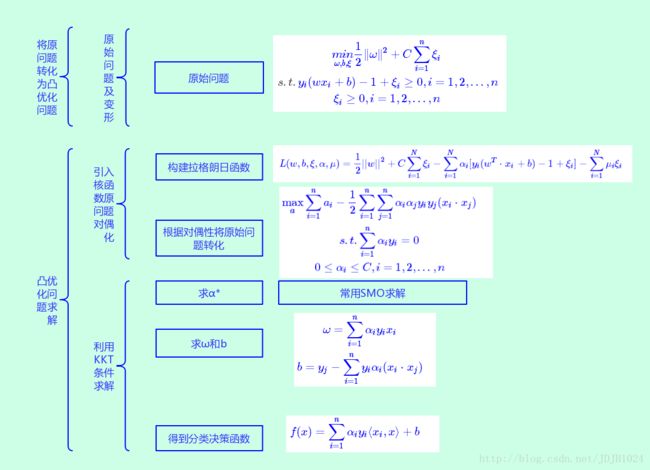
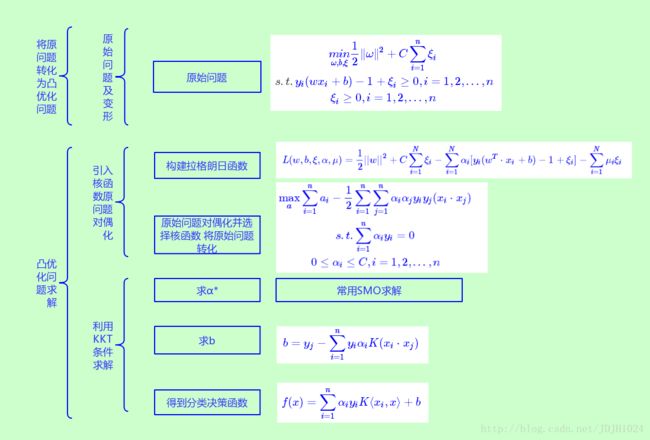
开门见山，先上流程图，看图说话，印象深刻

---

第二部分、对应求解流程图

1、 线性可分支持向量机求解流程图

2、 线性支持向量机求解流程图

3、利用核函数求解非线性支持向量机求解流程图

第三部分、理论及相关简要推导

logistic回归（或称作sigmoid）

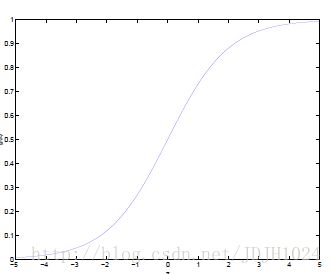
Logistic回归目的是从特征学习出一个0/1分类模型。是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上。 （目的是将区间缩小，以及中心重要化）

hθ(x)=g(θTx)=11+e−θTx(1.1)

• x： n维数据点；
• g： Logistic函数；
• θTx ：数据点xx的特征；

而 g(z)=11+e−z 的图像如下图所示：

从图中可以看出，Logister函数将范围为负无穷到正无穷的自变量z，映射到了区间(0, 1)。

{P(y=1|x;θ)=hθ(x)P(y=0|x;θ)=1−hθ(x)(1.2)

当判别一个新来的特征属于哪类 hθ(x) ，只需求 hθ(x) 即可，若 hθ(x) 大于1/2，数据点就是y=1的类；反之，属于y=0类。

如果我们只从特征 θT(x) 出发，那么我们所构建的模型的目标，就是让训练数据中，y=1的特征 θT ≫0，且y=0的特征 θT ≪0。Logistic回归，就是要学习得到θ，使得正例的特征远大于0，负例的特征远小于0。

为了使用方便，将Logistic回归进行变形。
将使用的结果标签y=0与y=1替换为y=−1与y=1。展开特征 θT(x) ，如下：

θTx=θ0+θ1x1+θ2x2+...+θnxn(x0=1)(1.3)

然后将上式(1.3)中的 θ0 替换为b，最后将后面的 θ1x1+θ2x2+...+θnxn 替换为 ωTx 得：

θTx=ωTx+b(1.4)

也就是说，除了分类值y，由y=0y=0变为y=−1y=−1之外，线性分类函数与Logistic回归的形式(公式1.1)没有区别。
我们可以将假设函数 hω,b(x)=g(ωTx+b) 中的g(z)函数做一个简化，将其简单映射到y=−1与y=1上。映射关系如下：

g(z)={1,z≥0−1,z<0(1.5)

举个栗子。如下图所示，有一二维平面，平面上有两种不同的数据，分别用圈和叉表示。因这些数据线性可分的，所以用一条直线将这两类数据劈开，这条直线就当作一个超平面，超平面一边的数据点所对应的y全是-1 ，另一边所对应的y全是1。

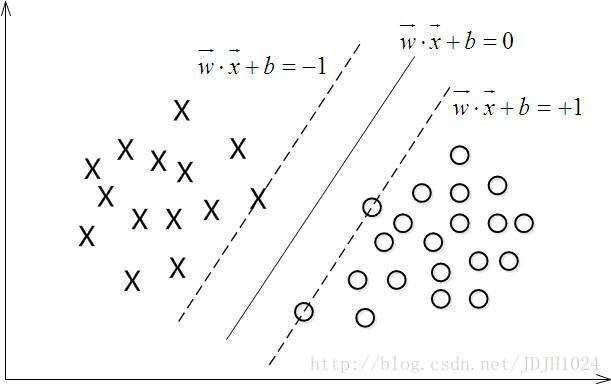
这个超平面可以用分类函数 f(x)=ωTx+b 表示，当f(x)等于0的时候，x便是位于超平面上的点，而f(x)大于0的点对应y=1的数据点，f(x)小于0的点对应y=−1的点，如上图所示.
在进行分类的时候，一个新的数据点x，将x代入f(x)中。若f(x)小于0，则将x的类属-1；如果f(x)大于0，则将x的类属1。

SVM函数间隔中 γ^=y(wTx+b)=yf(x)
y取1或-1有疑问，这个1或-1的分类标准起源于logistic回归。(对于二类问题，因为yy只取两个值，这两个是可以任意取的，只要是取两个值就行)

函数间隔与几何间隔

函数间隔(Functional Margin)

在超平面 ωTx+b=0 确定的情况下， ωTx+b 能够表示点x到超平面的距离远近，而通过观察 ωTx+b 的符号与类型标记y符号是否一致，判断分类是否正确。
所以，可以用 y⋅(ωT+b) 的正负性来判定分类是否正确。因此引出了函数间隔(Functional Margin)。
定义函数间隔如下：

γ^=y(ωTx+b)=yf(x)(2.1)

x ：特征；y：结果标签；

而超平面(ω,b)关于训练数据集T中所有样本点(x_i, y_i)的函数间隔最小值，便成为超平面ω,b)关于TT的函数间隔：

γ^=minγi^(i=1,...n)(2.2)

几何间隔(Geometrical Margin)

几何间隔由来，是由于函数间隔遇到了棘手的事，什么问题呢？例如成比例的改变ω,b（如将他们都增大10倍），则函数间隔f(x)的值变成了原来的10倍，但此时超平面却没有改变。因此只修炼函数间隔还不够闯荡江湖。
于是，我们可以对法向量ω加些约束，从而引出真正定义点到超平面的距离–几何间隔（geometrical margin）的概念。
假定对于一个点x，令其垂直投影到超平面上的对应点为 x0 ，ω是垂直于超平面的一个向量，为样本x到超平面的距离，如下图所示：

点xx在超平面的投影 x0

根据平面几何知识，得：

x=x0+γω∥ω∥(2.3)

又由于x0x0是超平面上的点，满足f(x0)=0，所以代入超平面的方程 ωTx+b=0 ,可得到 ωTx0+b=0 ,即 ωTx0=−b ,然后，令 x=x0+γω∥ω∥ 两端同时乘 ωT ,再根据 ωTx0=−b 与 ωTω=∥ω∥2 可得：

γ=ωT+b∥ω∥=f(x)∥ω∥(2.4)

为了得到 γ 的绝对值，令 γ 乘上对应的类别y，即可得出几何间隔（用 γ˜ 表示）的定义：

γ˜=yγ=γ^∥ω∥(2.5)

γ^ 是前文中的函数间隔。所以可以看出，几何间隔就是函数间隔除以∥ω∥，

最大间隔分类器(Maximum Margin Classifier)

(1) “间隔”的说明

对一个数据点进行分类，当超平面离数据点的”间隔”越大，分类的确信度(confidence)也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化该“间隔”值。

最大间隔分类器的定义

最大间隔分类器（maximum margin classifier）的目标函数可以定义为：

maxγ˜(3.1)

同时需要满足一些条件，根据间隔的定义，存在：

s.t.,yi(ωTxi+b)=γi^≥γ^,i=1,...,n(3.2)

s.t.s.t. 即Subject to的缩写，约束条件。
如果令函数间隔 γ^=1 ,则有 γ˜=1∥ω∥ ,且约束条件如上式,又有 max1∥ω∥ 的最大值，相当于求 12∥ω∥2 综上，上述目标函数便转化成了：

⎧⎩⎨min12∥ω∥2s.t.,yi(ωT+b)=γi^≥γ^,i=1,...,n(3.3)

现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。
可以用的QP (Quadratic Programming) 优化包进行求解。
此外，由于这个问题的特殊结构，还可以通过拉格朗日对偶性（Lagrange Duality）变换到对偶变量 (dual variable) 的优化问题，即通过求解与原问题等价的对偶问题（Dual Problem）得到原始问题的最优解，这就是线性可分条件下支持向量机的对偶算法。
这样做的好处在于： 对偶问题往往更容易求解； 可以自然的引入核函数，进而推广到非线性分类问题。
拉格朗日对偶型，简单的讲，就是通过给每一个约束条件加上一个拉格朗日乘子αα(Lagrange Multiplier)，定义拉格朗日函数如下式：

L(ω,b,α)=12∥ω∥2−∑i=1nαi[yi(ωTxi+b)−1](3.4)

对偶问题的求解
分为三个步骤：
1. 令L(ω,b,α)关于ω和b最小化；
2. 利用SMO算法求解对偶问题中的拉格朗日乘子，求对α的极大；
3. 求参数ω,b；

首先固定α，令LL关于ω,b最小化
对于式(3.4)，我们分别对ω,b求偏导数，即令 ∂L∂ω,∂L∂b 等于0。

∂L∂ω=0⇒ω=∑i=1nαiyixi∂L∂b=0⇒∑i=1nαiyi=0(3.5)

将上式(3.5)代入之前的式(3.4)中，得到：

L=12∑i,j=1nαiαjyiyjxTixj−∑i,j=1nαiαjyiyjxTixj−b∑i=1nαiyi+∑i=1nαi=∑i=1nαi−12∑i,j=1nαiαjyiyjxTixj(3.6)

利用SMO算法求解对偶问题中的拉格朗日乘子

求对α的极大值，就是关于对偶问题的最优化问题。经过上一个步骤的求取ω,b，得到的拉格朗日函数已经没有了变量ω,b，只存在变量α。 通过上面的式(3.6), 可以得到此时的目标函数：

maxα∑i=1nαi−12∑i=1nαiαjyiyjxTixjs.t.,αi≥0,i=1,...,n∑i=1nαiyi=0(3.7)

这时候通过SMO算法可以求解对偶问题中的拉格朗日乘子α。，求出了极值情况下的 αi ，就可以求出极值情况下的ω,b。
通过式(3.5)，可以计算出

ω∗=∑i=1nαiyixi

这里的 ω∗ 是指极值情况下的ω值，再然后可以求b值。由于对于边界上的支持向量有：

y(ωTx+b)=1

x 数据点是支持向量，参数yy表示支持向量所属类别（取值1或-1）。 而在y=−1,y=1的类别中，支持向量处于边界点。
由

⎧⎩⎨⎪⎪maxyi=−1ωTxi+b=−1minyi=1ωTxi+b=1

得到极值情况下的bb值，记为 b∗

b∗=12[maxyi=−1ω∗Txi+minyi=1ω∗Txi](3.8)

这样就求出了ω,b,α，便求出了我们在线性情况下的超平面f(x)。

线性支持向量机

软间隔最大化中，我们引入松弛变量 ξi≥0 ,允许样本错分。具体来说，现在的约束条件就变为了：

yi(w⋅xi+b)≥1−ξi

对于硬间隔SVM中的所有样本点，他们到分割平面的函数间隔都大于等于1。如今通过引入松弛变量，却允许他们函数间隔小于1了，即样本可以错分了。现在我们假设松弛变量 ξi 很大，则任意超平面都能满足条件了，这样显然是不合理的。因此原来的目标函数由 12||w||2 变成：

12||w||2+C∑i=1Nξi

其中C>0 称为惩罚函数，是对错分样本的惩罚。C很大时对错分样本的惩罚增大，C 很小时对错分样本的惩罚减小。（这样我们也可以将原始硬间隔中的目标函数看做是软间隔目标函数C 无穷大的情况，即硬间隔的错分代价无穷大，不允许错分）。这样，我们的学习问题就可以改写为：

minw,b,ξs.t12||w||2+C∑i=1Nξiyi(w⋅xi+b)≥1−ξi，i=1,2,…,Nξi≥0,i=1,2,…,N

同样，原始问题的拉格朗日函数为：

L(w,b,ξ,α,μ)=12||w||2+C∑i=1Nξi−∑i=1Nαi[yi(wT⋅xi+b)−1+ξi]−∑i=1Nμiξi

原始问题是拉个朗日的极大极小问题，对偶问题是极小极大问题，我们可以先求L(w,b,ξ,α,μ)L(w,b,ξ,α,μ)的极小值：

∂∂wL(w,b,ξ,α,μ)=w−∑i=1Nαiyixi=0⟹w=∑i=1Nαiyixi∂∂bL(w,b,ξ,α,μ)=−∑i=1Nαiyi=0⟹∑i=1Nαiyi=0∂∂ξiL(w,b,ξ,α,μ)=C−αi−ξi=0

将求导之后的极致条件带回原始的拉格朗日函数可以得到和硬间隔SVM一样的目标函数：

minw,b,ξL(w,b,ξ,α,μ)=∑i=1Nai−12∑i=1N∑j=1Nαiαjyiyj(xTi⋅xj)

但函数的约束条件却改变了，因此，对偶问题的优化问题为：

maxas.t.∑i=1Nai−12∑i=1N∑j=1Nαiαjyiyj(xTi⋅xj)∑i=1Nαiyi=00≤αi≤C,i=1,2,…,N

用SMO算法求出上式最小时对应的 α 向量的值 α∗ 向量.计算

w∗=∑i=1mα∗iyixi

找出所有的S个支持向量,即满足 0<αj<C 对应的样本 (xj,yj) ，通过  yj(∑i=1SαiyixTixj+b)=1 ，计算出每个支持向量 (xx,yj) 对应的 b ,计算出这些 b=yj−∑i=1Sαiyi(xTixj) .

线性不可分支持向量机

核函数

由于一般我们说的核函数都是正定核函数，这里我们直说明正定核函数的充分必要条件。一个函数要想成为正定核函数，必须满足他里面任何点的集合形成的Gram矩阵是半正定的。也就是说,对于任意的 xi∈χ，i=1,2,3...m K(xi,xj) 对应的Gram矩阵 K=[K(xi,xj)] 则K(x,z)是正定核函数。　
scikit-learn中默认可选的几个核函数

• 线性核函数: K(x,z)=x∙z
• 多项式核函数: K(x,z)=（γx∙z+r)d
• 高斯核函数: K(x,z)=exp(−γ||x−z||2)
• Sigmoid核函数: K(x,z)=tanh（γx∙z+r)
  输入是m个样本 (x1,y1),(x2,y2),...,(xm,ym), ,其中x为n维特征向量。y为二元输出，值为1，或者-1.
  　　　输出是分离超平面的参数 w∗和b∗ 和分类决策函数。
  　　算法过程如下：
  选择适当的核函数 K(x,z) 和一个惩罚系数 C>0 , 构造约束优化问题
  
  minα12∑i=1,j=1mαiαjyiyjK(xi,xj)−∑i=1mαi
  
  
  s.t.∑i=1mαiyi=0
  
  
  0≤αi≤C
  
  用SMO算法求出上式最小时对应的 α 向量的值 α∗ 向量.
  得到 w∗=∑i=1mα∗iyiϕ(xi) ，此处可以不直接显式的计算 w∗ 。
  找出所有的S个支持向量,即满足 0<αj<C 对应的样本 (xs,yj) ，通过  yj(∑i=1mαiyiK(xi,xj)+b)=1 ，计算出每个支持向量 (xj,yj) 对应的 b∗s ,计算出这些 b=yj−∑i=1mαiyiK(xi,xj) . 所有的 b∗s 对应的平均值即为最终的 b=1S∑i=1Sbj
   　　　　这样最终的分类超平面为： ∑i=1mα∗iyiK(x,xi)+b∗=0 ，最终的分类决策函数为： f(x)=∑i=1mαiyiK(x,xi)+b