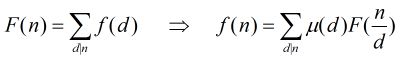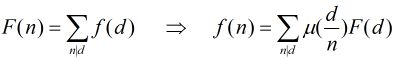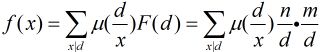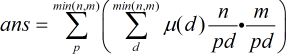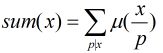Mobius反演(莫比乌斯反演)
莫比乌斯反演在数论中占有重要的地位,许多情况下能大大简化运算。那么我们先来认识莫比乌斯反演公式。
定理:![]() 和
和![]() 是定义在非负整数集合上的两个函数,并且满足条件
是定义在非负整数集合上的两个函数,并且满足条件![]() ,那么我们得到结论
,那么我们得到结论
在上面的公式中有一个![]() 函数,它的定义如下:
函数,它的定义如下:
(1)若![]() ,那么
,那么![]()
(2)若![]() ,
,![]() 均为互异素数,那么
均为互异素数,那么![]()
(3)其它情况下![]()
证明莫比乌斯反演公式的得出: 依旧通过例题来找规律
我们令 n=6;
那么 在计算 F(6)的时候,我们会用到 G(1) G(2) G(3) G(6)
我们考察者4个G
G(1) = F(1)
G(2) = F(1)+F(2)
G(3) = F(1)+F(3)
G(6) = F(1)+F(2)+F(3)+F(6)
观察上面可以发现 每个 G(n)都是由一些F(d)累加得到的
当我们需要逆向有G得到F(n)时,只需要将一些 与 F(n) 有关的 G进行容斥,最终组合得到F(n)!
比如 F(6) = G(6)-G(2)-G(3)+G(1)
根据上述公式知:F(6) =u(1) G(6)-u(3)G(2)-u(2)G(3)+u(6)G(1)
由 u 的公式知,u(1)=1, u(2)=(-1)^1=-1, u(3)=(-1)^1=-1, u(4)=(-1)^2=1;
则 F(6) = G(6)-G(2)-G(3)+G(1)
这类莫比乌斯反演的实质也就是容斥原理的应用!!
对于![]() 函数,它有如下的常见性质:
函数,它有如下的常见性质:
(1)对任意正整数![]() 有
有
(2)对任意正整数![]() 有
有
线性筛选求莫比乌斯反演函数代码。
void Init()
{
memset(vis,0,sizeof(vis));
mu[1] = 1;
cnt = 0;
for(int i=2; i
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 10000010;
bitset prime;
LL phi[N];
LL f[N];
int p[N];
int k;
void isprime()
{
k = 0;
prime.set();
for(int i=2; i>= 1;
for(int i=3; i 有了上面的知识,现在我们来证明莫比乌斯反演定理。
证明
证明完毕!
嗯,有了莫比乌斯反演,很多问题都可以简化了,接下来我们来看看莫比乌斯反演在数论中如何简化运算的。
题目:http://bz.cdqzoi.com/JudgeOnline/problem.php?id=2818
题意:给一个正整数![]() ,其中
,其中![]() ,求使得
,求使得![]() 为质数的
为质数的![]() 的个数,
的个数,![]() 。
。
分析:对于本题,因为是使得![]() 为质数,所以必然要枚举小于等于
为质数,所以必然要枚举小于等于![]() 的质数,那么对于每一个质数
的质数,那么对于每一个质数![]() ,只
,只
需要求在区间![]() 中,满足有序对
中,满足有序对![]() 互质的对数。
互质的对数。
也就是说,现在问题转化为:在区间![]() 中,存在多少个有序对使得
中,存在多少个有序对使得![]() 互质,这个问题就简单啦,因为
互质,这个问题就简单啦,因为
是有序对,不妨设![]() ,那么我们如果枚举每一个
,那么我们如果枚举每一个![]() ,小于
,小于![]() 有多少个
有多少个![]() 与
与![]() 互素,这正是欧拉函数。所以
互素,这正是欧拉函数。所以
我们可以递推法求欧拉函数,将得到的答案乘以2即可,但是这里乘以2后还有漏计算了的,那么有哪些呢?
是![]() 且为素数的情况,再加上就行了。
且为素数的情况,再加上就行了。
代码:
-
#include
-
#include
-
#include
-
#include
-
-
using
namespace
std;
-
typedef
long
long LL;
-
const
int N =
10000010;
-
-
bitset
prime;
-
LL phi[N];
-
LL f[N];
-
int p[N];
-
int k;
-
-
void isprime()
-
{
-
k =
0;
-
prime.
set();
-
for(
int i=
2; i
-
{
-
if(prime[i])
-
{
-
p[k++] = i;
-
for(
int j=i+i; j
-
prime[j] =
false;
-
}
-
}
-
}
-
-
void Init()
-
{
-
for(
int i=
1; i
-
for(
int i=
2; i
2) phi[i] >>=
1;
-
for(
int i=
3; i
2)
-
{
-
if(phi[i] == i)
-
{
-
for(
int j=i; j
-
phi[j] = phi[j] - phi[j] / i;
-
}
-
}
-
f[
1] =
0;
-
for(
int i=
2;i
-
f[i] = f[i
-1] + (phi[i]<<
1);
-
}
-
-
LL Solve(int n)
-
{
-
LL ans =
0;
-
for(
int i=
0; i
-
ans +=
1 + f[n/p[i]];
-
return ans;
-
}
-
-
int main()
-
{
-
Init();
-
isprime();
-
int n;
-
scanf(
"%d",&n);
-
printf(
"%I64d\n",Solve(n));
-
return
0;
-
}
嗯,上题不算太难,普通的欧拉函数就可以搞定,接下来我们来看看它的升级版。
题意:给定两个数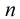 和
和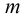 ,其中
,其中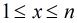 ,
,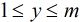 ,求
,求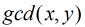 为质数的
为质数的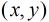 有多少对?其中
有多少对?其中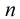 和
和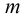 的范
的范
围是 。
。
分析:本题与上题不同的是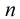 和
和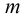 不一定相同。在这里我们用莫比乌斯反演来解决,文章开头也说了它能大大简化
不一定相同。在这里我们用莫比乌斯反演来解决,文章开头也说了它能大大简化
运算。我们知道莫比乌斯反演的一般描述为:
其实它还有另一种描述,本题也是用到这种。那就是:
好了,到了这里,我们开始进入正题。。。
对于本题,我们设
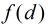 为满足
为满足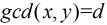 且
且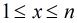 和
和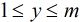 的
的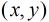 的对数
的对数
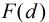 为满足
为满足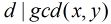 且
且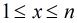 和
和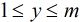 的
的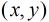 的对数
的对数
因为题目要求是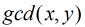 为质数,那么我们枚举每一个质数
为质数,那么我们枚举每一个质数 ,然后得到
,然后得到
如果直接这样做肯定TLE,那么我们必须优化。
到了这里,可以看出如果我们可以先预处理出所有的 对应的
对应的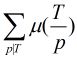 的值,那么本题就解决了。
的值,那么本题就解决了。
(1)如果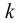 整除
整除 ,那么得到
,那么得到
(2)如果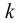 不整除
不整除 ,那么得到
,那么得到
-
#include
-
#include
-
#include
-
-
using
namespace
std;
-
typedef
long
long LL;
-
const
int N =
10000005;
-
-
bool vis[N];
-
int p[N];
-
int cnt;
-
int g[N],u[N],sum[N];
-
-
void Init()
-
{
-
memset(vis,
0,
sizeof(vis));
-
u[
1] =
1;
-
cnt =
0;
-
for(
int i=
2;i
-
{
-
if(!vis[i])
-
{
-
p[cnt++] = i;
-
u[i] =
-1;
-
g[i] =
1;
-
}
-
for(
int j=
0;j
-
{
-
vis[i*p[j]] =
1;
-
if(i%p[j])
-
{
-
u[i*p[j]] = -u[i];
-
g[i*p[j]] = u[i] - g[i];
-
}
-
else
-
{
-
u[i*p[j]] =
0;
-
g[i*p[j]] = u[i];
-
break;
-
}
-
}
-
}
-
sum[
0] =
0;
-
for(
int i=
1;i
-
sum[i] = sum[i
-1] + g[i];
-
}
-
-
int main()
-
{
-
Init();
-
int T;
-
scanf(
"%d",&T);
-
while(T--)
-
{
-
LL n,m;
-
cin>>n>>m;
-
if(n > m) swap(n,m);
-
LL ans =
0;
-
for(
int i=
1,last;i<=n;i=last+
1)
-
{
-
last = min(n/(n/i),m/(m/i));
-
ans += (n/i)*(m/i)*(sum[last]-sum[i
-1]);
-
}
-
cout<
endl;
-
}
-
return
0;
-
}
你可能感兴趣的:(ACM,----,数论,ACM,----,知识点)