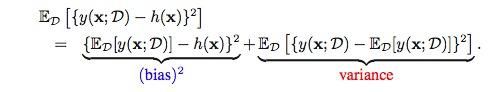自然语言处理(二)概率论信息论基础
概率论
概率
概率的统计定义
- 频率
事件A在n次重复随机试验中出现的次数与n的比值。 - 概率
在同一条件下做的大量重复试验中,若事件A发生的频率总是在一个确定的常数p附近摆动,并且逐渐稳定于p,那么数p就表示事件A发生的可能性大小,并成为事件A的概率.
概率的公理化定义
设E是随机试验,Ω是E的样本空间,对于E 的每一个事件A赋予一个实数值,
表示事件发生的可能性(记为 P ( A ) P(A) P(A)),则 P ( A ) P(A) P(A)为事件A的概率.概率必须满足如下公理:
- 非负性
- 规范性
P ( Ω ) = 1 P(\Omega)=1 P(Ω)=1 - 可加性
最大似然估计(MLE)
最大似然估计(Maximization likelihood estimation, MLE)
如果一个实验的样本空间是 s 1 , s 2 , … , s n s_1,s_2,\dots,s_n s1,s2,…,sn,在相同情况下重复实验N次,观察到样本 s k ( 1 ≤ k ≤ n ) s_k(1\leq k\leq n) sk(1≤k≤n)的次数维 n N ( s k ) n_N(s_k) nN(sk),则 s k s_k sk的相对频率为:
q N ( s k ) = n N ( s k ) N q_N(s_k) = \frac{n_N(s_k)}{N} qN(sk)=NnN(sk)
由于 ∑ i = 1 n n N ( s k ) = N \sum_{i=1}^nn_N(s_k) = N ∑i=1nnN(sk)=N,因此 ∑ i = 1 n q N ( s k ) = 1 \sum_{i=1}^nq_N(s_k)=1 ∑i=1nqN(sk)=1
当N越来越大时,相对频率 q N ( s k ) q_N(s_k) qN(sk)就越来越接近 s k s_k sk的概率 P ( s k ) P(s_k) P(sk).
lim N → ∞ q N ( s k ) = P ( s k ) \lim_{N\rightarrow \infty}q_N(s_k) = P(s_k) N→∞limqN(sk)=P(sk)
在N很大情况下,我们用相对频率来作为概率的估计值,即最大似然估计.
条件概率(conditional probability)
如果A和B是样本空间 Ω \Omega Ω上的两个事件, P ( B ) > 0 P(B)>0 P(B)>0,那么在给定B时A的条件概率 P ( A ∣ B ) P(A|B) P(A∣B)为
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P(A|B) = \frac{P(A\cap B)}{P(B)} P(A∣B)=P(B)P(A∩B)
全概率公式
P ( A ) = P ( ∪ i = 1 n A B i ) = ∑ i = 1 n P ( A B i ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A) = P(\cup_{i=1}^nAB_i) = \sum_{i=1}^nP(AB_i) = \sum_{i=1}^nP(B_i)P(A|B_i) P(A)=P(∪i=1nABi)=i=1∑nP(ABi)=i=1∑nP(Bi)P(A∣Bi)
贝叶斯法则(Bayes’ theorem)
P ( B i ∣ A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( B j ) P ( A ∣ B j ) P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\sum_{j=1}^nP(B_j)P(A|B_j)} P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)
贝叶斯决策理论
假设研究的分类问题有c个类别,各类别的状态用 w i w_i wi表示, i = 1 , 2 , … , c i=1,2,\dots,c i=1,2,…,c,对应于各类别 w i w_i wi出现的先验概率 P ( w i ) P(w_i) P(wi),在特征空间中观察到某一向量 x ˉ \bar{x} xˉ是d维特征空间上的某一点,且条件概率密度函数 P ( x ˉ ∣ w i ) P(\bar{x}|w_i) P(xˉ∣wi)是已知的.
那么用贝叶斯公式即可得到后验概率
p ( w i ∣ x ˉ ) = p ( x ˉ ∣ w i ) p ( w i ) ∑ j = 1 c p ( x ∣ w j ˉ p ( w j ) ) p(w_i|\bar{x}) = \frac{p(\bar{x}|w_i)p(w_i)}{\sum_{j=1}^cp(\bar{x|w_j}p(w_j))} p(wi∣xˉ)=∑j=1cp(x∣wjˉp(wj))p(xˉ∣wi)p(wi)
期望
E X = x 1 p 1 + x 2 p 2 + … EX = x_1p_1 + x_2p_2+\dots EX=x1p1+x2p2+…
E ( X ) = ∑ k = 1 ∞ x k p k E(X) = \sum_{k=1}^{\infty}x_kp_k E(X)=k=1∑∞xkpk
方差(variane)
描述随机变量的值偏离其期望的程度.
V a r ( X ) = E ( ( X − E ( X ) ) 2 ) = E ( X 2 ) − E 2 ( X ) \begin{aligned} Var(X) &= E((X-E(X))^2)\\ & = E(X^2) - E^2(X) \end{aligned} Var(X)=E((X−E(X))2)=E(X2)−E2(X)
偏置(Bias)
估计值与实际值的差.
偏置-方差分解
信息论
自信息
一个消息自身所包含的信息量,由事件的不确定性决定,定义为:
I ( x i ) = − log p ( x i ) = log 1 p ( x i ) I(x_i) = -\log p(x_i) = \log \frac{1}{p(x_i)} I(xi)=−logp(xi)=logp(xi)1
单位
- 取对数底为2,信息量的单位为比特
- 取对数底为e,信息量的单位为奈特,1奈特=1.443比特
- 工程上以10为底比较方便,信息量的单位为哈特莱,1哈特莱=3.322比特
信息熵(平均自信息)
随机变量 X X X由 A 1 … A n A_1\dots A_n A1…An共n个可能的状态,每个状态出现的机率分别为 p 1 , … p n p_1,\dots p_n p1,…pn,则随机变量 X X X的平均自信息量为
H ( X ) = − ∑ 1 n p i log p i H(X) = - \sum_1^np_i \log p_i H(X)=−1∑npilogpi
定义为 X X X的信息熵,记为 H ( X ) H(X) H(X).
通常熵的单位为二进制位比特,我们约定 0 log 0 = 0 0\log 0=0 0log0=0
X的具体内容与信息量无关,我们只关心概率分布.
熵
-
图
)
-
性质
0 ≤ H ( X ) ≤ log ∣ X ∣ 0\leq H(X) \leq \log|X| 0≤H(X)≤log∣X∣ -
第一个等号在X为确定值时成立
-
第二个等号在X均匀分布时成立
-
均匀分布时熵最大
联合熵
离散型二维随机变量XY的联合熵 H ( X , y ) H(X,y) H(X,y)定义为:
H ( X , Y ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log 2 p ( x , y ) H(X,Y) = - \sum_{x\in X}\sum_{y\in Y}p(x,y)\log_2p(x,y) H(X,Y)=−x∈X∑y∈Y∑p(x,y)log2p(x,y)
联合熵实际上就是描述一对随机变量平均所需要的信息量,是二维随机变量XY的不确定性度量.
互信息
一个事件 y j y_j yj所给出关于另一个事件 x i x_i xi的信息定义为互信息,表示为
I ( x i ; y j ) = I ( x i ) − I ( x i ∣ y j ) = log p ( x i ∣ y j ) p ( x i ) I(x_i;y_j)=I(x_i) - I(x_i|y_j) = \log \frac{p(x_i|y_j)}{p(x_i)} I(xi;yj)=I(xi)−I(xi∣yj)=logp(xi)p(xi∣yj)
互信息是已知事件 y j y_j yj后所消除的关于事件 x i x_i xi的不确定性的减少量,即Y的值透露了多少关于X的信息量.
条件熵
有两个变量:x,y.它们不是独立的,给定随机变量X的情况下,随机变量Y的条件熵的定义为:
H ( Y ∣ X ) = ∑ i p ( x i ) H ( H ∣ x i ) = − ∑ i ∑ j p ( x i ) p ( y j ∣ x i ) log p ( y j ∣ x i ) = − ∑ i ∑ j p ( x i y j ) log p ( y j ∣ x i ) \begin{aligned} H(Y|X) &= \sum_ip(x_i)H(H|x_i)\\ & = - \sum_i\sum_jp(x_i)p(y_j|x_i)\log p(y_j|x_i)\\ & = - \sum_i\sum_j p(x_iy_j)\log p(y_j|x_i) \end{aligned} H(Y∣X)=i∑p(xi)H(H∣xi)=−i∑j∑p(xi)p(yj∣xi)logp(yj∣xi)=−i∑j∑p(xiyj)logp(yj∣xi)
其中, H ( Y ∣ X ) H(Y|X) H(Y∣X)表示已知X时,Y的平均不确定性.
H ( Y ∣ X ) ≤ H ( Y ) H(Y|X)\leq H(Y) H(Y∣X)≤H(Y)
联合熵与信息熵、条件熵的关系
H ( X Y ) ≤ H ( X ) + H ( Y ) H(XY)\leq H(X) + H(Y) H(XY)≤H(X)+H(Y)
当二维随机变量X、Y相互独立时,等号成立.
相对熵
两个概率分布 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)的相对熵定义为:
D ( p ∣ ∣ q ) = ∑ x ∈ X p ( x ) log p ( x ) q ( x ) D(p||q) = \sum_{x\in X}p(x)\log \frac{p(x)}{q(x)} D(p∣∣q)=x∈X∑p(x)logq(x)p(x)
相对熵通常被用来衡量两个随机分布的差距,当两个随机分布相同时,其相对熵为0,当两个随机分布的差别增大时,其相对熵也增大.
交叉熵
一个随机变量 X p ( x ) X~p(x) X p(x), q ( x ) q(x) q(x)为近似 p ( x ) p(x) p(x)的概率分布,随机变量X和模型q之间的交叉熵定义为:
H ( X , q ) = H ( X ) + D ( p ∣ ∣ q ) = − ∑ x p ( x ) log q ( x ) H(X,q) = H(X) + D(p||q) = - \sum_x p(x)\log q(x) H(X,q)=H(X)+D(p∣∣q)=−x∑p(x)logq(x)
交叉熵的概念用以衡量估计模型与真实概率分布之间的差异.
困惑度
设计语言模型时,通常用困惑度来代替交叉熵衡量语言模型的好坏,给定语言L的样本 l 1 m = l 1 ⋯ l n l_1^m = l_1\cdots l_n l1m=l1⋯ln,L的困惑度 P P q PP_q PPq定义为:
P P q = 2 H ( L , q ) ≈ 2 − 1 2 log q ( l 1 n ) = [ q ( l 1 n ) ] − 1 / n PP_q = 2^{H(L,q)}\approx2^{-\frac{1}{2}\log q(l_1^n)} = [q(l_1^n)]^{-1/n} PPq=2H(L,q)≈2−21logq(l1n)=[q(l1n)]−1/n
语言模型设计的任务就是寻找困惑度最小的模型,使其接近真实的语言.