计算机图形学基础 : 可见面判别算法

可见面判别算法分为两种类型， 称为物空间算法和像空间算法。物空间算法将场景中的各对象和对象的各个组成部件相互进行比较，从而最终判别出哪些面是可见的； 而像空间算法则在投影平面上逐点判断各像素所对应的可见面。

后向面判别

快速简便的判别多面体后向面，设点(x, y, z)满足：

Ax + By + Cz + D < 0

则该点在多边形面的后面，A、B、C、D是多边形面的平面参数。

可以通过考察多边形面的法向量 N的方向来简化后向面测试， Vview为下图左所示由相机位置出发的观察向量，则当   Vview ● N > 0 时，该多边形为后向面。然后，如果将对象描述转换到投影坐标系后，观察方向平行于观察坐标系中的Zv轴，这时候仅需考虑 N在Z轴上的z分量即可。

在沿着Zv轴反向观察的右手观察系统中(上图右)，若法向量 N的z分量C 满足 C < 0，则该多边形为一个后向面。同时，我们无法观察到法向量的z分量 C = 0的所有多边形面， 因为观察方向与该面相切。 因此，一旦某多边形面的法向量的z分量值： C <= 0， 即可判定其为一个后向面。 如果采用的是左手坐标系， 以上方法同样适用，平面参数A、B、C、D可由顺时针方向标识的多边形顶点坐标计算出来（右手坐标系中为逆时针方向），同样的，如果观察方向与z轴正向一致，则后向面的法向量为远离试点的方向，由 C >= 0来进行判别。

深度缓存算法(Z-Buffer算法)

该算法沿着观察系统的z轴来计算各对象距离观察平面的深度，在这个算法里，不仅需要有帧缓冲区来存放每个像素的亮度值， 还需要有一个Z缓冲区来存放每个像素的深度值，算法的大概流程是 ：

帧缓冲区置为背景色;

Z缓冲区置为最小Z值;

for (各个多边形)

{

扫面转换该多边形；

for (多边形所覆盖的每个像素(x, y) )

{

计算多边形在该像素的深度之Z(x, y);

if (Z(x，y)大于Z缓冲区在(x, y)处的值)

{

把Z(x,y)存入Z缓冲区中的(x, y)处;

把多边形在(x, y)处的亮度值存入帧缓冲区的(x, y)处;

}

}

}

多边形在各个像素处的深度值可从顶点的深度值用增量方法求出，对于一个给定的多边形，在某一点(x, y)的深度值可借助于平面方程ax+by+cz+d = 0表示为：

z = (-d - ax - by) / c

在(x, y)处求出z值是z1， 则在 (x + △x, y)处的 z值为 z1 - a/c(△X)， a/c为常数。一般取△x = 1，因此，在已知(x, y)处的深度值时， 求(x + 1, y) 处的深度值只要做一次减法。

A缓存算法

A缓存(A-Buffer)算法是Z-Buffer算法的延伸，这种深度缓存的扩充是一种反走样、区域平均、可见性检测方法。 该过程的缓存区域称为累计缓存，因为它除了深度值外还用于存储各种表面数据。

Z-Buffer的缺点是，在每个像素点只能找到一个可见面，即只能处理非透明表面，无法处理多个表面的累计强度值，对于下图所示的透明表面，这种处理又是必需的。A缓存算法对深度缓存算法进行了扩充，使其每一个位置均对应于一个表面链表，不仅可以考虑各像素点处多个表面的强度值，还可以对对象的边界进行反走样处理。

A缓存中每个单元均包含两个域：

● 深度域 —— 存储一个正的或负的实数。

● 强度域 —— 存储表面的强度信息或指针值。

若深度域值为正，则该值表示覆盖该像素点的唯一表面的深度。 表面数据场中存储各种表面信息，如该点的表面颜色和像素覆盖率。 如果A缓存某一位置的深度场是负的，则表明有多个表面对该像素的颜色有贡献，此时颜色场存储一个表面数据链表的指针，A 缓存中的表面信息包括：

● RGB强度分量

● 透明性参数（透明度）

● 深度

● 覆盖度

● 表面的标识名

● 其他表面绘制参数

A缓存可以按照类似于深度缓存算法来创建，沿每条扫描线确定各像素点所对应的覆盖表面。 表面可分割为多边形网格，并利用像素边界对其进行裁剪。采用不透明因子和表面覆盖度，以 所有覆盖表面作用的平均值来计算每个像素点处的强度值。

（a）表示只有一个表面覆盖该像素； （b）有多个表面覆盖该像素

扫描线算法

这个像空间的隐藏面消除算法沿各扫描线计算并比较场景的深度值，逐条处理各条扫描线时，首先判别与其相交的所有表面的可见性，然后计算各重叠表面的深度值以找到离观察平面最近的表面，一旦确定了某像素点所对应的可见面，可以得到该点的强度值，并置入帧缓存。

存储在多边形表中的信息用于处理表面，边表中包含场景中各线段的端点坐标、线段斜率的倒数和指向多边形表中对应多边形的指针; 多边形表中则包含各个多边形面的平面方程系数、表面材料特性、其他表面数据以及可能有的指向边表的指针，为了加速查找与扫描线相交的表面，可以在处理时建立一张活化边表，仅包含与当前扫描线相交的边，并将它们按x升序排列。 然后，可以给各个多边形面定义一个可设定为“on”或“off”的标志位，用来表示扫描线上某像素点位于多边形内或者多边形外。扫描线有左向右处理，在凸多边形的面投影的左边界处，标志位为“on”，表示开始；而在右边界处，标志位为“off”，表示结束。

在上图中，对于扫描线1对应的活化边表中，包含了边表中的边AB、BC、EH和FG的信息。在AB与BC之间沿线的像素点，只有S1的标志位为“on”，因此，可将面S1的颜色信息直接从其表面特性和列出的条件中计算，而无需计算深度值。同样在EH和FG之间，只有S2的标志位为“on”，而扫描线1的其余部分与所有表面均不相交，这些像素的强度值应置为背景强度。

对于扫描线2和3，活化边表包含AD、EH、BC和FG，在扫描线2上AD与EH之间的部分，只有S1的标志位为“on”，而在EH和BC之间的部分，所有面的标志位都为“on”，因此，在碰到EH边时必须用平面参数来为两个表面计算深度值，假设S1表面深度值小于S2表面的深度值，因此将面S1的颜色值沿扫描线置入像素中，直到边BC。然后将面S1的标志位置为“off”，再将面S2的颜色值置入刷新缓存，直到边FG。 逐条处理扫描线时，可利用线段的连贯性，扫描线3和扫描线2具有相同的活化边表，由于线段交点没有发生变化，因此无需再边EH与BC之间再进行深度计算。

BSP树算法

BSP树算法是一种有效的判别对象可见性的算法，适用于场景中对象位置固定不变，仅视点移动的情况。

利用BSP树来判别表面的可见性，主要操作在每次分割空间时，判别该表面相对于视点与分割平面的位置关系，即位于其后面还是前面。

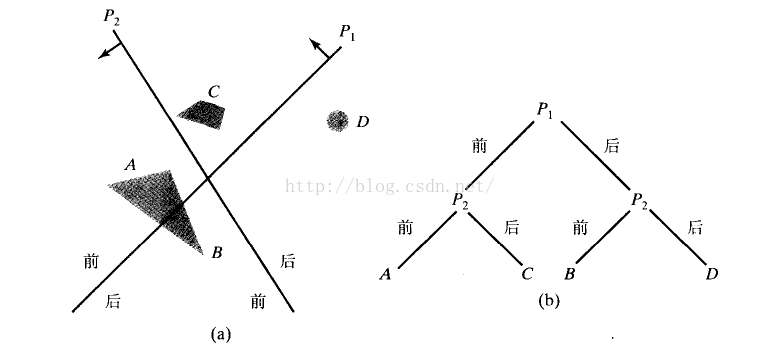
在上图中，首先P1将空间分割为两部分，相对于观察方向，一组对象位于P1的后面而另一组位于P1的前面，如果某个对象与P1相交，将该对象分为两部分A和B，A与C位于P1之前，B与D位于P1之后； 平面P2对空间进行再一次分割，表示为一颗二叉树，在树上，对象用叶节点表示，位于分割平面前方的对象位于左分支，后面的位于右分支。

一旦BSP树创建完毕，可按先右节点后左节点的次序处理该树，树上的面按由后往前次序显示。

区域细分算法

该算法通过对代表单个表面部分的投影区域定位而充分利用了场景中区域的连贯性。应用此方法连续的将整个观察平面区域细分为越来越小的矩形单元，直至每个矩形区域仅包含单个可见面的投影、不含任何表面或该区域只有一个像素大小。

一个表面与细分后的观察平面区域的关系有四种：

● 包围表面 —— 完全包含该区域的表面

● 重叠表面 —— 部分位于该区域内，部分位于该区域外的表面

  ● 内含表面 —— 完全在该区域内的表面

● 分离表面 —— 完全在该区域外的表面

根据上述四种情况，来给出表面的可见性测试，若下面的条件之一为真，则无需再对区域进行分割：

1：该区域没有内含、重叠或包围表面（所有表面均为区域的分离表面）。

2：该区域只有一个内含表面、重叠表面或者包围表面。

3：该区域有一个在其边界内遮挡了其他所有表面的包围表面。

开始的时候，可以检查所有表面的包围矩形与区域边界的关系，可以识别内含和包围表面，但需要求交操作才能识别重叠和分离表面。若包围矩形与区域边界有交点，则还需进行另外的检查来判别表面是否为包围型、重叠型或分离型，一旦判别出某单个表面是内含、重叠或包围型的，就将其像素强度值置入帧缓存的相应位置。

上述 3的测试方法，将表面根据它们离观察平面的最近距离进行排序，对于所有考察区域内的包围表面，计算其最大深度。如果某一包围表面距观察平面的最大深度小于该区域内其他所有表面的最小深度，则满足该测试方法。

八叉树算法

将物体按照八叉树表示的时候，通常按由前往后的顺序将八叉树节点映射到观察表面，从而消除隐藏面。

在上左图中，编号为0、 1、 2、 3的体元位于前面（相对于观察方向），4、5、6、7位于后面，0、1、2、3体元的尾部的表面和4567体元都可能被前面的体元的表面遮挡。

对于图中的观察方向，可按照体元顺序0、1、2、3、4、5、6、7来处理八叉树节点中的数据可消除隐藏面，实际上是对八叉树的深度优先遍历，因此，在4、5、6、7之前访问代表体元0、1、2、3的节点。 同样，0号体元中的前面4个子体元将在后面4个子体元之前被访问，对于每个八分体元的八叉树遍历将按照这个顺序进行。

如果在一个八叉树节点中设置颜色值，则仅当帧缓存中对应于该节点的像素为止尚未设置值时才置入。这样，缓存中仅置入前面的颜色值，如果位置无效，则不置入任何值。任何被完全遮挡的节点都将不再对其处理，也不会访问它的子节点。