打印机模拟（灰度篇）

打印机模拟（灰度篇）

零．前言

中山大学 软件工程 课程多媒体技术作业——图像抖动。包含技术简介和python代码实现。写于2017年9月23日。

一．背景

打印图片时，普通的黑白针式打印机是不能打出我们常用的256级灰度的点来的，因为针打是靠针击打色带从而在纸上形成黑点的，这样的设备只能选择打印一个点或者不打印一个点，因此不会打出灰点来。但如果我们需要的正是一个灰度图像，难道只能非黑即白了吗？技术上我们亟需解决这样的问题，而由此诞生图像抖动技术能让我们通过黑白两色，看到一张正常的灰色图像。

二．方法

图像抖动只要利用的是人眼的特性。在一个密集的二值点阵中，0代表的黑色点越密集，图像在这个位置附近显得颜色越深，即深灰色乃至黑色。反之，1代表的白色的点越密集，图像在这个位置附近显得颜色越浅，即浅灰色乃至白色。这实际是种误差扩散的方法。

在打印一张灰度级数为256的图片时时，每个像素用一个矩阵来表示它的灰度，如果要无差异的表示一个像素的颜色的话，我们需要用一个16*16的矩阵。因为这样一个矩阵可以出现0到256个1或0，即能表示257个灰度值，甚至多于256。

当然也可以用小于这个大小的矩阵表示，但越小的矩阵失真的程度就越大。

还有一种算法是，缩减灰度级别后，将新得到的像素值和原像素值的差按比例（可以均分）分到该点的领域上，即周围的八个像素点。这样也能使图像变得较平滑。

三．重点介绍

我重点关注了前一种算法，即用空间换亮度的算法。我尝试用python实现了这个算法。用python是因为它对图像处理支持的API很多，写起来会比较轻松，如果是C的话就麻烦多了。但之前我并没有正式接触过python，因此我花了一个下午从语法开始，到能运用一些API解决问题。因为很多还是没了解，例如python的二维数组和矩阵类型之间的异同，以及API的参数和返回值的含义，所以实现起来可能会比较笨拙。

主要方法是用2*2或3*3或4*4的矩阵来表示每个像素点，并且矩阵内存有一个唯一的整数（0到n^2-1,n为矩阵的边长)。在处理每个像素点时，将该像素值映射到0到n^2-1之间的一个整数上去。然后将对应的矩阵上所存整数值小于该值的点设为1，其余为0。这样就能处理一个像素点了，其它类推。

四．实验关键代码

主要难点还是API不熟悉吧。也就实现了将一张灰度图分别用2*2和3*3和4*4的矩阵来表示每个像素，模拟了打印机的打印过程。
代码如下：

from PIL import Image
from numpy import *
from pylab import *
import numpy as np
import matplotlib.pyplot as plt

filename = 'test.png';
im = Image.open(filename).convert("L");
width, height = im.size;

data = array(im);
data.reshape(height, width);

dim = 4;#2, 3 or 4
if dim == 2:
    paint = [[0, 2], [3, 1]];
elif dim == 3:
    paint = [[0, 7, 2], [8, 4, 5], [3, 6, 1]];
elif dim == 4:
    paint = [[0, 8, 2, 10], [12,4,14,6], [3,11,1,9],[15,7,13,5]];

n = dim * height;
m = dim * width;
top_color = 255;
arr = [None] * n;
for i in range(len(arr)):  
    arr[i] = [0] * m;

div = top_color / dim / dim;
for i in range(0, height):
    for j in range(0, width):
        tmp = int(data[i][j] / div);
        for ii in range(0, dim):
            for jj in range(0, dim):
                if paint[ii][jj] < tmp:
                    arr[dim * i + ii][dim * j + jj] = top_color;
                else :
                    arr[dim * i + ii][dim * j + jj] = 0;

new_matrix = mat(arr);
new_im = Image.fromarray(new_matrix.astype(np.ubyte));
new_im.show();

五．实验结果

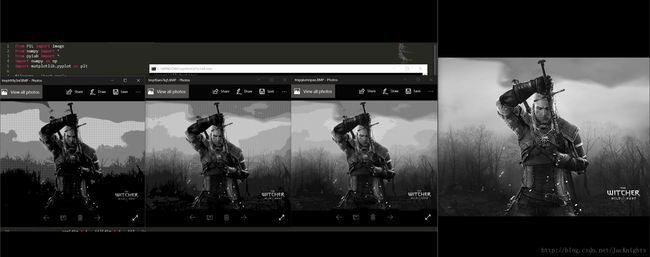
实验结果截图如下，从左到右分别是2*2、3*3和4*4的矩阵表示的抖动后的图像。可以看到尽管都有明显的瑕疵，但是随着矩阵增大，图片清晰度还是明显上去了。

再配上一张和原图的对比，差距还是很明显的。