HDU1055Color a tree

Color a Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2270 Accepted Submission(s): 824

Problem Description
Bob is very interested in the data structure of a tree. A tree is a directed graph in which a special node is singled out, called the “root” of the tree, and there is a unique path from the root to each of the other nodes.

Bob intends to color all the nodes of a tree with a pen. A tree has N nodes, these nodes are numbered 1, 2, …, N. Suppose coloring a node takes 1 unit of time, and after finishing coloring one node, he is allowed to color another. Additionally, he is allowed to color a node only when its father node has been colored. Obviously, Bob is only allowed to color the root in the first try.

Each node has a “coloring cost factor”, Ci. The coloring cost of each node depends both on Ci and the time at which Bob finishes the coloring of this node. At the beginning, the time is set to 0. If the finishing time of coloring node i is Fi, then the coloring cost of node i is Ci * Fi.

For example, a tree with five nodes is shown in Figure-1. The coloring cost factors of each node are 1, 2, 1, 2 and 4. Bob can color the tree in the order 1, 3, 5, 2, 4, with the minimum total coloring cost of 33.

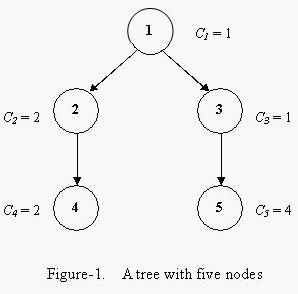
Given a tree and the coloring cost factor of each node, please help Bob to find the minimum possible total coloring cost for coloring all the nodes.

Input
The input consists of several test cases. The first line of each case contains two integers N and R (1 <= N <= 1000, 1 <= R <= N), where N is the number of nodes in the tree and R is the node number of the root node. The second line contains N integers, the i-th of which is Ci (1 <= Ci <= 500), the coloring cost factor of node i. Each of the next N-1 lines contains two space-separated node numbers V1 and V2, which are the endpoints of an edge in the tree, denoting that V1 is the father node of V2. No edge will be listed twice, and all edges will be listed.

A test case of N = 0 and R = 0 indicates the end of input, and should not be processed.

Output
For each test case, output a line containing the minimum total coloring cost required for Bob to color all the nodes.

Sample Input

5 1
1 2 1 2 4
1 2
1 3
2 4
3 5
0 0

Sample Output

33
证明过程转载自https://my.oschina.net/locusxt/blog/210536
首先给出自己在网上找的证明过程：

（以下已经把每个点看成一个点集，独立的一个点可看做只有一个元素的点集，每个点集中的点有顺序，并且需要依次连续地染色，也就是染完第一个点后，需要立刻依次染之后的点）
每次找一个最大权值的非根点集，将它和它的父点集合并。新的点集的权值是（新点集中所有点的权值和）/（新点集中点的个数）。这里点集中的点有顺序，合并时，子点集的点放在父点集的点后面。
进行上述步骤，直到只剩下一个根点集。这时候，根点集中点的顺序，就是染色的顺序。

证明：
(i)先看每个都是点的情况。给出一个结论：如果这棵树中有最大权值点x（非根），那么一旦x的父节点已经染色，就应该立刻染x。
这比较好证：设x的父节点为y，染色顺序为ya…bx,a…b这一段是别的一些可以染的点。这个染色顺序的意思是说染完x的父节点y之后，先染了一些别的点，再染x。
如果我们把b和x的染色顺序交换，显然是可行的，并且会更优：比较xb和bx，使用前者我们的收益（少掉的开销）是Cx-Cb，x少等了1的时间，b多等了1的时间。显然，收益Cx-Cb是正的，因为x的权值是当前最大的。这样我们也可以证，染完y之后应该立刻染x，所以可以把y和x合并成一个点集。
(ii)现在看都看做点集的情况，证明合并后以平均权值作为新的权值是合理的。
一个结论：如果这棵树中有最大平均权值点集X（非根），那么一旦X的父点集已经染色，就应该立刻染X。
这和(i)类似：设X的父子集Y，染色顺序YA…BX，A…B是别的一些可以染的点集。下证B和X染色顺序互换可以更优。设B的总权值为SB，点数为NB;X的为SX和NX。XB和BX比较，使用前者的收益是SX×NB- SB×NX，这相当与X中的每个点都少等待NB时间，而B中的每个点都多等了NX的时间。又因为X是最大平均权值点集，所以权值SX/NX>SB/NB，所以可以确保收益SX×NB-SB×NX是正的。
所以这样合并没有问题。
再给出自己的代码：

#include 
typedef struct TREE {
    int p;//父本
    int c;//初始值
    int t;//所需时间
    double w;//我将其理解为权重,这个是贪心的关键
}tree;
int n, r, sum;
tree a[1001];
int find()
{
    double max = 0;
    int q;
    for (int i = 1; i <= n; i++)
    {
        if (i == r)//根结点无父本
            continue;
        if (a[i].w > max)
            max = a[i].w, q = i;
    }
    return q;
}
int main()
{
    while (scanf("%d%d", &n, &r) != EOF)
    {
        if (n == 0 && r == 0)
            break;
        int N = n, i = 1;
        sum = 0;
        while (N--)
        {
            scanf("%d", &a[i].c);
            a[i].w = a[i].c;
            sum = sum + a[i].c;
            a[i].t = 1;
            ++i;
        }
        N = n - 1;
        int s, e;
        while (N--)
        {
            scanf("%d%d", &s, &e);
            a[e].p = s;
        }
        i = n;
        while (i > 1)
        {
            int t = find();
            sum = sum + a[t].c * a[a[t].p].t;
            a[t].w = 0;
            for (int k = 1; k <= n; k++)
            {
                if (a[k].p == t)
                    a[k].p = a[t].p;
            }
            a[a[t].p].c = a[a[t].p].c + a[t].c;
            a[a[t].p].t = a[a[t].p].t + a[t].t;
            a[a[t].p].w = (double)a[a[t].p].c / a[a[t].p].t;
            --i;
        }
        printf("%d\n", sum);
    }
    return 0;
}