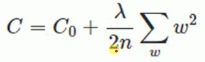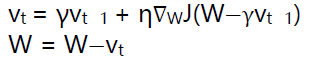深度学习框架TensorFlow学习与应用（四）——拟合问题、优化器

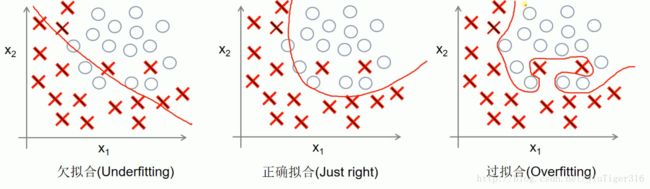
一、拟合

1）回归问题：

过拟合尽量去通过每一个样本点，误差为零。假如有一个新的样本点：

会发现过拟合的偏差会很大。

2）分类问题：

同样的当得到新的样本点后，过拟合的错误率可能会提高。

3）防止过拟合：

1.增加数据集

2.正则化方法，在代价函数后面加一个正则项

3.Dropout：训练时，在每一次迭代时使得一些神经元工作，一些神经元不工作。测试时再使用所有的神经元。

4）使用Dropout避免过拟合：

例如：创建一个神经网络，2000个神经元的隐藏层，后面又是2000个神经元的隐藏层，之后是1000个神经元的隐藏层，最后是10个输出层。用来进行前部分的MINST数据集分类训练。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#载入数据集
mnist=input_data.read_data_sets("D:\BaiDu\MNIST_data",one_hot=True)

#每个批次的大小
batch_size=100
#计算一共有多少个批次
n_batch=mnist.train.num_examples//batch_size

#定义placeholder
x=tf.placeholder(tf.float32,[None,784])
y=tf.placeholder(tf.float32,[None,10])#标签
keep_prob=tf.placeholder(tf.float32)

#创建一个的神经网络，2000个神经元的隐藏层，后面又是2000个神经元的隐藏层，只有是1000个神经元的隐藏层，最后是10个输出层
W1=tf.Variable(tf.truncated_normal([784,2000],stddev=0.1))
b1=tf.Variable(tf.zeros([2000])+0.1)
L1=tf.nn.tanh(tf.matmul(x,W1)+b1)
L1_drop=tf.nn.dropout(L1,keep_prob)

W2=tf.Variable(tf.truncated_normal([2000,2000],stddev=0.1))
b2=tf.Variable(tf.zeros([2000])+0.1)
L2=tf.nn.tanh(tf.matmul(L1_drop,W2)+b2)
L2_drop=tf.nn.dropout(L2,keep_prob)

W3=tf.Variable(tf.truncated_normal([2000,1000],stddev=0.1))
b3=tf.Variable(tf.zeros([1000])+0.1)
L3=tf.nn.tanh(tf.matmul(L2_drop,W3)+b3)
L3_drop=tf.nn.dropout(L3,keep_prob)

W4=tf.Variable(tf.truncated_normal([1000,10],stddev=0.1))
b4=tf.Variable(tf.zeros([10])+0.1)

prediction=tf.nn.softmax(tf.matmul(L3_drop,W4)+b4)

#二次代价函数
#loss=tf.reduce_mean(tf.square(y-prediction))
loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用梯度下降法
train_step=tf.train.GradientDescentOptimizer(0.2).minimize(loss)

#初始化变量
init=tf.global_variables_initializer()

#结果存放在一个布尔型列表中
correct_prediction=tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#比较两个参数大小，相同为true。argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))#将布尔型转化为32位浮点型，再求一个平均值。true变为1.0，false变为0。

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(31):
        for batch in range(n_batch):
            batch_xs,batch_ys=mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys,keep_prob:1.0})#keep_prob为1.0表示所有的神经元都是工作的

        test_acc=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels,keep_prob:1.0})#测试数据算出来的准确率
        train_acc=sess.run(accuracy,feed_dict={x:mnist.train.images,y:mnist.train.labels,keep_prob:1.0})#训练集算出的准确率
        print("Iter "+str(epoch)+",Testing Accuracy "+str(test_acc)+",Training Accuracy "+str(train_acc))

由于神经元较多，运行会很慢很慢。。。。。
结果是：

Iter 0,Testing Accuracy 0.9469,Training Accuracy 0.956455
Iter 1,Testing Accuracy 0.9567,Training Accuracy 0.974745
Iter 2,Testing Accuracy 0.9617,Training Accuracy 0.982473
Iter 3,Testing Accuracy 0.9632,Training Accuracy 0.986273
Iter 4,Testing Accuracy 0.9654,Training Accuracy 0.988509
Iter 5,Testing Accuracy 0.9679,Training Accuracy 0.989818
Iter 6,Testing Accuracy 0.9676,Training Accuracy 0.991
Iter 7,Testing Accuracy 0.9675,Training Accuracy 0.991655
Iter 8,Testing Accuracy 0.9681,Training Accuracy 0.992164
Iter 9,Testing Accuracy 0.9688,Training Accuracy 0.992509
Iter 10,Testing Accuracy 0.968,Training Accuracy 0.993018
Iter 11,Testing Accuracy 0.9692,Training Accuracy 0.993255
Iter 12,Testing Accuracy 0.968,Training Accuracy 0.993527
Iter 13,Testing Accuracy 0.9688,Training Accuracy 0.993745
Iter 14,Testing Accuracy 0.9699,Training Accuracy 0.994018
Iter 15,Testing Accuracy 0.9697,Training Accuracy 0.994109
Iter 16,Testing Accuracy 0.9693,Training Accuracy 0.9942
Iter 17,Testing Accuracy 0.9695,Training Accuracy 0.994345
Iter 18,Testing Accuracy 0.9692,Training Accuracy 0.9944
Iter 19,Testing Accuracy 0.9696,Training Accuracy 0.994436
Iter 20,Testing Accuracy 0.9704,Training Accuracy 0.994527
Iter 21,Testing Accuracy 0.9704,Training Accuracy 0.994582
Iter 22,Testing Accuracy 0.97,Training Accuracy 0.994727
Iter 23,Testing Accuracy 0.9698,Training Accuracy 0.994764
Iter 24,Testing Accuracy 0.97,Training Accuracy 0.994855
Iter 25,Testing Accuracy 0.9701,Training Accuracy 0.994891
Iter 26,Testing Accuracy 0.9705,Training Accuracy 0.995036
Iter 27,Testing Accuracy 0.9707,Training Accuracy 0.995145
Iter 28,Testing Accuracy 0.9707,Training Accuracy 0.995273
Iter 29,Testing Accuracy 0.9705,Training Accuracy 0.995364
Iter 30,Testing Accuracy 0.9705,Training Accuracy 0.9954

之后使用Dropout：

sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys,keep_prob:0.7})

得到：

Iter 0,Testing Accuracy 0.9179,Training Accuracy 0.912891
Iter 1,Testing Accuracy 0.9328,Training Accuracy 0.9284
Iter 2,Testing Accuracy 0.9344,Training Accuracy 0.935255
Iter 3,Testing Accuracy 0.9409,Training Accuracy 0.940891
Iter 4,Testing Accuracy 0.9439,Training Accuracy 0.944909
Iter 5,Testing Accuracy 0.9471,Training Accuracy 0.949964
Iter 6,Testing Accuracy 0.9499,Training Accuracy 0.952018
Iter 7,Testing Accuracy 0.9502,Training Accuracy 0.953527
Iter 8,Testing Accuracy 0.9548,Training Accuracy 0.957055
Iter 9,Testing Accuracy 0.9563,Training Accuracy 0.958418
Iter 10,Testing Accuracy 0.9566,Training Accuracy 0.959309
Iter 11,Testing Accuracy 0.958,Training Accuracy 0.961364
Iter 12,Testing Accuracy 0.9593,Training Accuracy 0.962527
Iter 13,Testing Accuracy 0.96,Training Accuracy 0.964055
Iter 14,Testing Accuracy 0.9607,Training Accuracy 0.965745
Iter 15,Testing Accuracy 0.9622,Training Accuracy 0.966818
Iter 16,Testing Accuracy 0.9624,Training Accuracy 0.967655
Iter 17,Testing Accuracy 0.9641,Training Accuracy 0.968564
Iter 18,Testing Accuracy 0.964,Training Accuracy 0.969564
Iter 19,Testing Accuracy 0.9633,Training Accuracy 0.969945
Iter 20,Testing Accuracy 0.9661,Training Accuracy 0.971182
Iter 21,Testing Accuracy 0.9664,Training Accuracy 0.972127
Iter 22,Testing Accuracy 0.9682,Training Accuracy 0.972709
Iter 23,Testing Accuracy 0.968,Training Accuracy 0.973145
Iter 24,Testing Accuracy 0.9662,Training Accuracy 0.974345
Iter 25,Testing Accuracy 0.9695,Training Accuracy 0.974436
Iter 26,Testing Accuracy 0.9689,Training Accuracy 0.975164
Iter 27,Testing Accuracy 0.9689,Training Accuracy 0.9756
Iter 28,Testing Accuracy 0.9699,Training Accuracy 0.976091
Iter 29,Testing Accuracy 0.9696,Training Accuracy 0.976545
Iter 30,Testing Accuracy 0.9719,Training Accuracy 0.977236

可以看出：

使用Dropout后，模型的收敛速度变慢，准确率上升的速度慢。那么为什么还要使用Dropout呢？通过对比两次的测试准确率和训练准确率，可以看到，没有使用Dropout的方法测试准确率和训练准确率相差比较大，这就是过拟合的问题，使用了Dropout就可以进行优化。另外，本部分提供的例子并没有很好的体现出Dropout的优势，两者的准确率的对比不明显，如果使用大型卷积神经网络进行样本训练，结果会更明显。

---

二、优化器

tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.ProximalGradientDescentOptimizer
tf.train.ProximalAdagradOptimizer
tf.train.RMSPropOptimizer

各种优化器对比：
标准梯度下降法：标准梯度下降先计算所有样本汇总误差，然后根据总误差来更新权值。
随机梯度下降法：随机梯度下降随机抽取一个样本来计算误差，然后更新权值。
批量梯度下降法：批量梯度下降算是一种折中的方案，从总样本中选取一个批次（比如一共有10000个样本，随机选取100个样本作为一个batch），然后计算这个batch的总误差，根据总误差来更新权值。

接下来具体讲一下几个优化器：

W:要训练的参数

J（W）：代价函数

：代价函数的梯度

：学习率

1）SGD（随机梯度下降法）：

2）Momentum：

当前权值的改变会受到上一次权值改变的影响，类似于小球向下滚动的时候带上了惯性。这样可以加快小球的向下的速度。

3）NAG（Nesterov accelerated gradient）：

NAG在TF中跟Momentum合并在同一个函数tf.train.MomentumOptimizer中，可以通过参数配置启用。在Momentum中小球会盲目跟从下坡的梯度，容易发生错误，所以我们需要一个更聪明的小球，这个小球提前知道它要去哪里，它还要知道走到坡底的时候速度慢下来而不是又冲上另一个坡。我们可以提前计算下一个位置的梯度，然后使用到当前位置。

4）Adagrad：

它是基于SGD的一种算法，它的核心思想是对比比较常见的数据给予它比较小的学习率去调整参数，对于比较罕见的数据给予它较大的学习率去调整参数。它很适合应用于数据稀疏的数据集（比如一个图片的数据集，有10000张狗的照片，10000张猫的照片，只有100张大象的照片）。
Adagrad主要的优势在于不需要人为的调节学习率，它可以自动调节。它的缺点在于，随着迭代次数的增多，学习率也会越来越低，最终会趋向于0。

5）RMSprop：
RMS（Root Mean Square）是均方根的缩写。

RMSprop借鉴了一些Adagrad的思想，不过这里RMSprop只用到了前t-1次梯度平方的平均值加上当前梯度的平方的和的开平方作为学习率的分母。这样RMSprop不会出现学习率越来越低的问题，而且也能自己调节学习率，并且可以有一个比较好的效果。

6）Adadelta：

使用Adadelta我们甚至不需要设置一个默认的学习率，在Adadelta不需要使用学习率也可以达到一个很好的效果。

7）Adam：

就像Adadelta和RMSprop一样Adam会存储之前衰减的平方梯度，同时它也会保存之前衰减的梯度。经过一些处理之后再使用类似Adadelta和RMSprop的方式更新参数。

8）举例：

更改学习率、优化器种类、迭代次数、神经元等对比一下。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#载入数据集
mnist=input_data.read_data_sets("D:\BaiDu\MNIST_data",one_hot=True)

#每个批次的大小
batch_size=100
#计算一共有多少个批次
n_batch=mnist.train.num_examples//batch_size

#定义两个placeholder
x=tf.placeholder(tf.float32,[None,784])
y=tf.placeholder(tf.float32,[None,10])#标签

#创建一个简单的神经网络
W=tf.Variable(tf.zeros([784,10]))
b=tf.Variable(tf.zeros([10]))
prediction=tf.nn.softmax(tf.matmul(x,W)+b)

#二次代价函数
loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用优化器
#train_step=tf.train.GradientDescentOptimizer(0.2).minimize(loss)
train_step=tf.train.AdamOptimizer(0.001).minimize(loss)
#初始化变量
init=tf.global_variables_initializer()

#结果存放在一个布尔型列表中
correct_prediction=tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#比较两个参数大小，相同为true。argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))#将布尔型转化为32位浮点型，再求一个平均值。true变为1.0，false变为0。

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys=mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})

        acc=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
        print("Iter "+str(epoch)+",Testing Accuracy "+str(acc))

结果：

Iter 0,Testing Accuracy 0.8988
Iter 1,Testing Accuracy 0.9125
Iter 2,Testing Accuracy 0.916
Iter 3,Testing Accuracy 0.919
Iter 4,Testing Accuracy 0.9221
Iter 5,Testing Accuracy 0.9227
Iter 6,Testing Accuracy 0.9271
Iter 7,Testing Accuracy 0.9269
Iter 8,Testing Accuracy 0.9274
Iter 9,Testing Accuracy 0.9282
Iter 10,Testing Accuracy 0.929
Iter 11,Testing Accuracy 0.9291
Iter 12,Testing Accuracy 0.9304
Iter 13,Testing Accuracy 0.9288
Iter 14,Testing Accuracy 0.9302
Iter 15,Testing Accuracy 0.9304
Iter 16,Testing Accuracy 0.93
Iter 17,Testing Accuracy 0.9315
Iter 18,Testing Accuracy 0.9311
Iter 19,Testing Accuracy 0.9321
Iter 20,Testing Accuracy 0.9311

可以看出，同之前使用梯度下降法相比，使用Adam的收敛性和准确率更好。