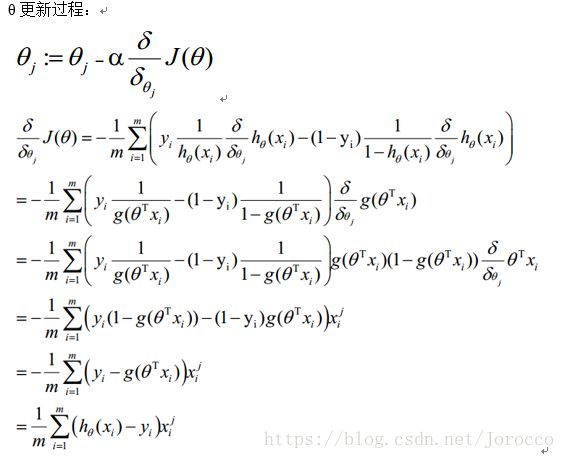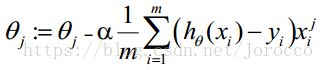机器学习算法总结（二）

1、KNN算法
KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：

同时，KNN通过依据k个对象中占优的类别进行决策，而不是单一的对象类别决策。这两点就是KNN算法的优势。
接下来对KNN算法的思想总结一下：就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：
1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

2、贝叶斯算法
贝叶斯定理是关于随机事件 A 和 B 的条件概率：

其中P(A|B)是在 B 发生的情况下 A 发生的可能性。
在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。
按这些术语，贝叶斯定理可表述为：
后验概率 = (相似度 * 先验概率)/标淮化常量
也就是说，后验概率与先验概率和相似度的乘积成正比。
另外，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：
后验概率 = 标淮相似度 * 先验概率
条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。
联合概率表示两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为联合概率。

朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素是因为其思想基础的简单性：就文本分类而言，它认为词袋中的两两词之间的关系是相互独立的，即一个对象 的特征向量中每个维度都是相互独立的。例如，黄色是苹果和梨共有的属性，但苹果 和梨是相互独立的。这是朴素贝叶斯理论的思想基础。现在我们将它扩展到多维的情况：

朴素贝叶斯分类的正式定义如下：
1．设 x={a1,a2,…,am}为一个待分类项，而每个 a 为 x 的一个特征属性。
2．有类别集合 C={y1,y2,…,yn}。
3．计算 P( y1|x) ,P( y2|x),…, P( yn|x)。
4．如果 P( yk|x) =max{P( y1|x),P( y2|x),…, P( yn|x)}，则 x∈yk。（当x所属概率最大时则为该类）
那么现在的关键就是如何计算第 3 步中的各个条件概率。我们可以这么做：
(1) 找到一个已知分类的待分类项集合，也就是训练集。
(2) 统计得到在各类别下各个特征属性的条件概率估计。即：
P(a1|y1) , P(a2|y1),…, P(am|y1);
　　　　　　　　P(a1|y2) , P(a2|y2),…, P(am|y2);
　　　　　　　　P(am|yn) , P(am|yn),…, P(am|yn)。
　(3) 如果各个特征属性是条件独立的(或者我们假设它们之间是相互独立的)，则根 据贝叶斯定理有如下推导：
　
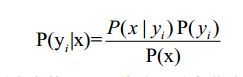
　因为分母对于所有类别为常数，只要将分子最大化皆可。又因为各特征属性是条件独立的，而每个a为x的一个特征属性（每个属性的概率相乘就得到x的概率），所以有：
　
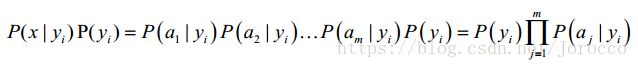
　根据上述分析，朴素贝叶斯分类的流程可以表示如下：
　第一阶段：训练数据生成训练样本集：TF-IDF
　第二阶段：对每个类别计算 P(yi)，先验概率
　第三阶段：对每个特征属性计算所有划分的条件概率，即P（a1|yi）…
　第四阶段：对每个类别计算 P( x | yi ) P( yi )
　第五阶段：以 P( x | yi ) P( yi ) 的最大项作为 x 的所属类别

#!/usr/bin/python
# -*-coding:utf-8-*-
# __author__ = 'ShenJun'
import numpy as np
from os import listdir
class Bayes:
    def __init__(self):
        self.length=-1
        self.labelcount=dict()
        self.vectorcount=dict()
    def fit(self,dataSet:list,labels:list):
        if((len(dataSet))!=len(labels)):
            raise ValueError("您输入的测试数组跟类别数组长度不一致")
        self.length=len(dataSet[0])#获取测试数据特征值的长度
        labelsnum=len(labels)#类别所有的数量
        norlabels=set(labels)#不重复类别的数量
        for item in norlabels:
            thislabel=item
            #求得当前类别占所有类别的概率
            self.labelcount[thislabel]=labels.count(thislabel)/labelsnum
        for vevtor,label in zip(dataSet,labels):
            if(label not in self.vectorcount):
                self.vectorcount[label]=[]
            self.vectorcount[label].append(vevtor)
        print("训练结束")
        return self
    def btest(self,TestData,labelSet):
        #testData为一维数组
        if(self.length==-1):
            raise ValueError("您还没有进行训练，请先训练")
        #计算testdata分别为各个类别的概率
        lbDict=dict()
        for thislb in labelSet:
            p=1
            alllabel=self.labelcount[thislb]#得到当前标签占所有类别的概率
            allvector=self.vectorcount[thislb]
            vnum=len(allvector)#得到属于同一类别的个数，也就是训练集中同一类别的同一个特征能有多少种表示法（因为属于同一类别并不代表每一个特征表示的都一样，它只是从整体上而言是一样的）
            allvector=np.array(allvector).T
            for index in range(0,len(TestData)):
                vector=list(allvector[index])#将训练集的表示同一个特征的点列成一个列表（每个点并不完全一样）
                #vector.count(TestData[index]统计出训练集中该特征的表示有多少个与测试集的表示一样
                p=p*(vector.count(TestData[index])/vnum)#一个一个特征的计算概率
            lbDict[thislb]=p*alllabel
        thislabel=sorted(lbDict,key=lambda x:lbDict[x],reverse=True)[0]
        return thislabel
'''
贝叶斯公式因为分母都一样，所以只要分子最大则表明属于该类的可能性最大
'''

'''
贝叶斯算法实现手写体识别
'''
#加载数据
def datatoarray(fname):
    arr=[]
    fh=open(fname)
    #因为图片文本是32乘32的，将每一个像素点的值都放入一个长度为1024的列表中
    for i in range(0,32):
        thisline=fh.readline()
        for j in range(0,32):
            arr.append(int(thisline[j]))
    return arr
#取文件名前缀，通过分隔文件名得到标签即真实数字
def seplabel(fname):
    filestr=fname.split(".")[0]
    label=int(filestr.split("_")[0])
    return label

#建立训练数据
def traindata():
    labels=[]
    trainfile=listdir("F:\\网络爬虫\\视频课程\\源码\\源码\\第7周\\testandtraindata\\traindata")
    num=len(trainfile)
    #长度为1024列  每一行存储一个文件
    #用一个数组存储所有训练数据，行是文件总数，列是1024
    trainarr=np.zeros((num,1024))
    for i in range(0,num):
        thisfname=trainfile[i]
        thislabel=seplabel(thisfname)
        labels.append(thislabel)
        trainarr[i,:]=datatoarray("F:\\网络爬虫\\视频课程\\源码\\源码\\第7周\\testandtraindata\\traindata\\"+thisfname)
    return trainarr,labels
bys=Bayes()
#训练数据
train_data,labels=traindata()
bys.fit(train_data,labels)
#测试
thisdata=datatoarray("F:\\网络爬虫\\视频课程\\源码\\源码\\第7周\\testandtraindata\\testdata\\8_90.txt")
labelsall=[0,1,2,3,4,5,6,7,8,9]
'''
#识别单个手写体数字
# rst=bys.btest(thisdata,labelsall)
# print(rst)
'''
#识别多个手写体数字
testfileall=listdir("F:\\网络爬虫\\视频课程\\源码\\源码\\第7周\\testandtraindata\\testdata")
num=len(testfileall)
for i in range(0,num):
    thisfilename=testfileall[i]
    thislable=seplabel(thisfilename)
    thisdataarray=datatoarray("F:\\网络爬虫\\视频课程\\源码\\源码\\第7周\\testandtraindata\\testdata\\"+thisfilename)
    label=bys.btest(thisdataarray,labelsall)
    x=0
    if(label!=thislable):
        x+=1
        print("此次出错")
print(x)
print("错误率是："+str(float(x)/float(num)))

3、回归算法

3.1 逻辑回归

3.1.1 什么是逻辑回归
逻辑回归其实是一个分类算法而不是回归算法。通常是利用已知的自变量来预测一个离散型因变量的值（像二进制值0/1，是/否，真/假）。简单来说，它就是通过拟合一个逻辑函数（logit fuction）来预测一个事件发生的概率。所以它预测的是一个概率值，自然，它的输出值应该在0到1之间，即主要用于二分类问题。

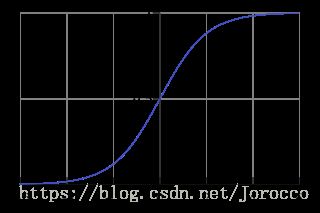
它的核心思想是，如果线性回归的结果输出是一个连续值，而值的范围是无法限定的，那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢。而如果输出结果是 (0,1) 的一个概率值，这个问题就很清楚了。我们在数学上找了一圈，还真就找着这样一个简单的函数了，就是很神奇的sigmoid函数(如下)：

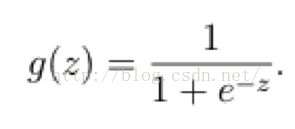
3.1.2 逻辑回归优缺点
优点：
1）速度快，适合二分类问题
2）简单易于理解，直接看到各个特征的权重
3）能容易地更新模型吸收新的数据
缺点：
对数据和场景的适应能力有局限性，不如决策树算法适应性那么强
3.1.3 逻辑回归和多重线性回归的区别
Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。
这一家族中的模型形式基本上都差不多，不同的就是因变量不同。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

• 如果是连续的，就是多重线性回归
• 如果是二项分布，就是Logistic回归
• 如果是Poisson分布，就是Poisson回归
• 如果是负二项分布，就是负二项回归

3.1.4 回归常规步骤

• 寻找h函数（即预测函数）
• 构造J函数（损失函数）

• 想办法使得J函数最小并求得回归参数（θ）

  寻找h函数（即预测函数）
  
  
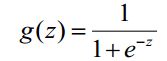
  对于线性边界的情况，边界形式如下：
  
  其中，训练数据为向量
  
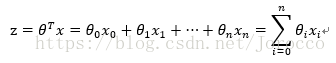
  最佳参数
  
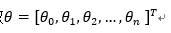
  构造预测函数为：
  
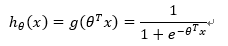
  函数h(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：
  P(y=1│x;θ)=h_θ (x)
  P(y=0│x;θ)=1-h_θ (x)

构造损失函数J（m个样本，每个样本具有n个特征）

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

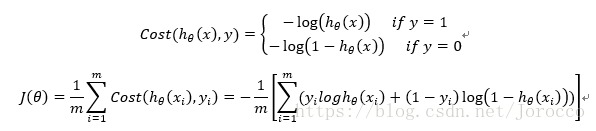
损失函数推导过程：
1） 求代价函数
概率综合起来写成：

取似然函数为：

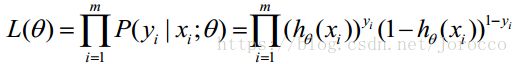
对数似然函数为：

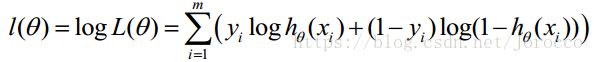
最大似然估计就是求使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。
在Andrew Ng的课程中将J(θ)取为下式，即：

梯度下降法求解最小值

θ更新过程可以写成：

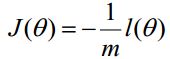
3.1.5 向量化
ectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。
向量化过程：
约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。
θ更新过程可以改为：

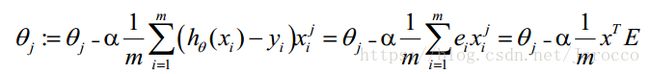
综上所述，Vectorization后θ更新的步骤如下：
1、求 A=x*θ
2、求 E=g(A)-y

3.1.6 正则化
（1） 过拟合问题
过拟合即是过分拟合了训练数据，使得模型的复杂度提高，繁华能力较差（对未知数据的预测能力）
下面左图即为欠拟合，中图为合适的拟合，右图为过拟合。

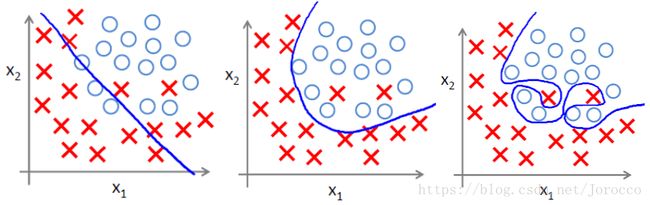
（2）过拟合主要原因
过拟合问题往往源自过多的特征
解决方法
1）减少特征数量（减少特征会失去一些信息，即使特征选的很好）

• 可用人工选择要保留的特征；
• 模型选择算法；
  2）正则化（特征较多时比较有效）
• 保留所有特征，但减少θ的大小

正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化项就越大。
正则项可以取不同的形式，在回归问题中取平方损失，就是参数的L2范数，也可以取L1范数。取平方损失时，模型的损失函数变为：

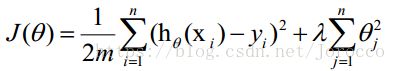
lambda是正则项系数：

• 如果它的值很大，说明对模型的复杂度惩罚大，对拟合数据的损失惩罚小，这样它就不会过分拟合数据，在训练数据上的偏差较大，在未知数据上的方差较小，但是可能出现欠拟合的现象；
• 如果它的值很小，说明比较注重对训练数据的拟合，在训练数据上的偏差会小，但是可能会导致过拟合。
  正则化后的梯度下降算法θ的更新变为：
  
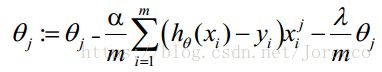
  3.1.7 python实现逻辑回归

from sklearn.linear_model import LogisticRegression
Model = LogisticRegression()
Model.fit(X_train, y_train)
Model.score(X_train,y_train)
# Equation coefficient and Intercept
Print(‘Coefficient’,model.coef_)
Print(‘Intercept’,model.intercept_)
# Predict Output
Predicted = Model.predict(x_test)