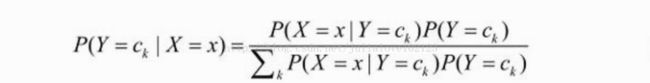机器学习十大算法---9. 朴素贝叶斯
---------------------------------------------------------------------------------------------------------------------
贝叶斯定理
贝叶斯理论指事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的;
朴素贝叶斯
朴素贝叶斯方法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率(Maximum A Posteriori)最大的输出y。
朴素贝叶斯算法原理
朴素贝叶斯方法是一种生成模型,对于给定的输入x,通过学习到的模型计算后验概率分布P(Y=c_k | X=x),将后验概率最大的类作为x的类输出。其中后验概率计算根据贝叶斯定理进行:
朴素贝叶斯分类模型
开发流程
算法特点
优点: 在数据较少的情况下仍然有效,可以处理多类别问题。
缺点: 对于输入数据的准备方式较为敏感。
适用数据类型: 标称型数据。引例
假如我是一个质检员,现在接到了三箱零件需要检验,其中第一箱10个零件,第二箱20个零件,第三箱15个。我的检验的结果是第一箱有1个不合格,第二箱有3个不合格,第三箱2个不合格。
下午领导来随手拿了一个零件,那领导拿到这个件合格的概率有多大?
样本空间:3个箱子,记 Ai 为从第i个箱子拿的零件(i=1,2,3);
拿到正品事件:记为B ;P(合格):记为 P(B)。
则:P(B) = P(A1)*P(B | A1) + P(A2) *P(B | A2) + P(A3)*P(B | A3)
= (1/3) * 9/10 + (1/3) * 17/20 + (1/3) * 13/15
= 0.872
注:P(B | A1) 是条件概率:零件来自于第一个箱子的条件下,并且它为合格件的概率。
结果是领导拿到了一个正品,那这个合格品来自于箱子1的概率是多大?这个问题也就是求 P(A1 | B),即取到合格品B的情况下,来自于A1的概率。
P(A1 | B)称为求解逆向概率,它对应的正向概率:P(B | A1),转化一下:P(A1| B) = P(A1*B) / P(B)
注:A1*B 事件表示从第一个箱子抽取且合格,则 P(A1*B) = P(A1) * P(B | A1) = (1/3) * 9/10 = 0.3;P(A1*B),也可记为:P(A1,B),称为联合概率;因此,P(A1| B) = 0.3 / 0.872 = 0.344
这个已知B发生,然后,预测B来自于哪里,便是贝叶斯公式做的事。
贝叶斯公式
以上例子的样本空间由A1,A2 ,A3 组成,如果将划分到由 n 个部分组成,抽中一个合格件为本次随机试验的事件B,明显地,P(Ai) 和 P(B)都大于零,则事件B发生后,找出它属于哪个类别的计算公式如下:
贝叶斯公式是要找出组成发生事件B的各个样本空间,然后预测事件B的发生来自于Ai的概率。
其中 P(Ai) 称为原因的先验概率,可以看到它是在不知道事件B是否发生的情况下获取的概率。
而 P(Ai | B) 是原因的后验概率,它是在知道了事件B发生的条件下,判断原因 Ai 发生的概率有多大。可以看到,一般地,如果对样本空间做了大于1的划分,即:
根据贝叶斯公式,可推出:
也就是说在获取了进一步的信息B后,原因的后验概率一般大于原因的先验概率。
注意到在贝叶斯公式中,要求后验概率 P(classification | data) ,利用贝叶斯公式将其其转化为求解 :
P(classification) * P(data | classification) / P(data)
这种求解模式在机器学习中被称为:生成式(generative models)模式。
注意到
P(data) 是与类标记无关的量,可以看做是一个常数;
P(classification) 表达了各类样本所占的比例,根据大数定律,当训练集包含了充足的独立同分布样本时,P(classification)可以通过各类样本出现的频率来进行估计。
实例介绍:
验证过了10个苹果,主要根据大小,颜色和形状这三个特征,来区分是好是坏,如下:
| # | 大小 | 颜色 | 形状 | 标签 |
|---|---|---|---|---|
| 1 | 小 |
青色 | 非规则 | 否 |
| 2 | 大 | 红色 | 非规则 | 是 |
| 3 | 大 | 红色 | 圆形 | 是 |
| 4 | 大 | 青色 | 圆形 | 否 |
| 5 | 大 | 青色 | 非规则 | 否 |
| 6 | 小 | 红色 | 圆形 | 是 |
| 7 | 大 | 青色 | 非规则 | 否 |
| 8 | 小 | 红色 | 非规则 | 否 |
| 9 | 小 | 青色 | 圆形 | 否 |
| 10 | 大 | 红色 | 圆形 | 是 |
测试集上要预测的某个样本如下:
| # | 大小 | 颜色 | 形状 | 标签 |
|---|---|---|---|---|
| 11 | 大 |
青色 | 圆形 | ? |
假定,苹果的三个特征:大小,颜色,形状,是相互独立的。
类条件概率
贝叶斯公式中一个非常重要的概率:P(x | c) 是条件概率,是在 c 发生的条件下,x 出现的概率。c是整个数据集中所有种类中的一种,比如是好苹果,这个类; x 是在好苹果这个类别中所有属性的可能取值,在上面这个例子中,一共有3个属性,每个属性有2个不同取值,因此共有8个不同组合,所以 x 就是在8种不同取值中每个取值的样本个数。
其中 i 为1~8中的某个取值,在本例中为:大,红色,圆形
P(x | c) 这种概率为:类条件概率,它等于在训练集中属于类别 c 的所有样本中,所有属性组合的样本出现的概率。
属性独立假设
类的后验概率 P(x | c) 计算公式如下:
在特征间相互独立的前提假定下,类条件概率的计算公式便可以进一步推导为如下:
其中,d是样本的所有属性个数,类条件概率等于每个属性的类条件概率的乘积
因此,联合得到如下式子:
朴素贝叶斯分类器
由于对所有类别来说,P(x)是相同的,因此贝叶斯分类器的目标函数进一步化简为如下:
称上面式子为朴素贝叶斯分类器的目标函数,明显地,朴素贝叶斯分类器的训练学习的过程便是基于训练数据,求得
类的先验概率P(c),并且为每个属性求得类条件概率,然后相乘取最大值的过程。
解决1:简单解决
求解之前的苹果问题:
先验概率 P(c) :
P(c=好果)= 4/10
P(c=一般) = 6/10
每个属性的类条件概率:这个类别下的样本中对应这个属性的样本个数除以这个类别下的样本个数,因此:
P(大小=大 | c=好果) = 3/4
P(颜色=红色 | c=好果) = 4/4
P(形状=圆形 | c=好果) = 3/4
P(大小=大 | c=一般) = 3/6
P(颜色=红色 | c=一般) = 1/6
P(形状=圆形 | c=一般) = 2/6
因此:
P(c=好果) * P(大小=大 | c=好果) * P(颜色=红色 | c=好果) * P(形状=圆形 | c=好果)
= 4/10 * 3/4 * 4/4 * 3/4
= 0.225
P(c=一般) * P(大小=大 | c=一般) * P(颜色=红色 | c=一般) * P(形状=圆形 | c=一般)
= 6/10 * 3/6 * 1/6 * 2/6
= 0.0167
显然,0.225 > 0.0167 所以:这个苹果为好果。
so:
| # | 大小 | 颜色 | 形状 | 标签 |
|---|---|---|---|---|
| 11 | 大 |
青色 | 圆形 | ? |
通过已知的数据集发现: P(颜色=青色 | c=好果) = 0,那么无论 P(其他属性 | c=好果) 取值为多大,哪怕在其他属性上取值多么像好果,相乘后都为0,这显然不太合理,这种方法的预测发现了一个问题:某个样本的属性值并未出现在训练集中,导致尽管要预测的这个苹果看起来很像是好果,但是朴素贝叶斯目标函数的结果仍为0,最终被划分为一般的苹果,有些时候这并不是合理的。
拉普拉斯修正
上面通过这个例子折射处一个问题:训练集上,很多样本的取值可能并不在其中,但是这不并代表这种情况发生的概率为0,因为未被观测到,并不代表出现的概率为0 。
正如上面的样本,看其他两个属性很可能属于好苹果,但是再加上颜色:青色,这三个属性取值组合在训练集中并未出现过,所以朴素贝叶斯分类后,这个属性取值的信息抹掉了其他两个属性的取值,在概率估计时,通常解决这个问题的方法是要进行平滑处理,常用拉普拉斯修正。
拉普拉斯修正的含义是,在训练集中总共的分类数,用 N 表示;di 属性可能的取值数用 Ni 表示,因此原来的先验概率 P(c) 的计算公式由:
被拉普拉斯修正为:
类的条件概率P(x | c) 的计算公式由:
被拉普拉斯修正为:
解决2:部分样本未出现
用拉普拉斯修正后的公式计算,先验概率 P(c) ,
P(c = 好果)= (4+1) / (10+2) = 5/12
P(c = 一般) = (6+1) / (10+2) = 7/12
每个属性的类条件概率:
P(大小=大 | c=好果) = (3+1)/(4+2) = 4/6
P(颜色=青色 | c=好果) = (0+1)/(4+2) = 1/6
P(形状=圆形 | c=好果) = (3+1) / (4+2) = 4/6
P(大小=大 | c=一般) = (3+1) /( 6+2) = 4/8
P(颜色=青色 | c=一般) = (5+1)/(6+2) = 6/8
P(形状=圆形 | c=一般) = (2+1)/(6+2) = 3/8
因此:
P(c=好果) * P(大小=大 | c=好果) * P(颜色=青色 | c=好果) * P(形状=圆形 | c=好果)
= 5/12 * 4/6 * 1/6 * 4/6
= 0.031
P(c=一般) * P(大小=大 | c=一般) * P(颜色=红色 | c=一般) * P(形状=圆形 | c=一般)
= 7/12 * 4/8 * 6/8 * 3/8
= 0.082
因此预测结果还是一般的果子,这是训练集学习后得到的结果,可能与原来的结果正好吻合,但是并不代表拉普拉斯修正是没有必要的,有时候预测的结果会和原来直接某项为0的结果不一样,可以看到拉普拉斯修正后,原来为0的结果被平滑的过渡为0.031,这起到了修正的作用。
朴素贝叶斯分类器的基本原理有一个假定为:各个属性条件是独立的假设,但是在现实任务中此假设往往难以成立!
故产生了又一种分类算法:半朴素贝叶斯分类。
朴素贝叶斯分类器的一个重要假定:分类对应的各个属性间是相互独立的,然而在现实应用中,这个往往难以做到,那怎么办呢?因此,适当考虑一部分属性间的相互依赖关系,这种分类称为半朴素贝叶斯分类,其中最常用的策略:假定每个属性仅依赖于其他最多一个属性,称其依赖的这个属性为其超父属性,这种关系称为:独依赖估计(ODE)。
因此,对某个样本x 的预测朴素贝叶斯公式就由如下:
修正为如下的半朴素贝叶斯分类器公式:
从上式中,可以看到类条件概率 P(xi | c) 修改为了 xi 依赖于分类c 和 一个依赖属性pai 。
半朴素贝叶斯例子
基于类c和类外的依赖属性pai的条件概率计算公式如下:
属性的依赖关系定义如下:
大小的依赖属性为:形状,且属性取值为大时依赖形状为圆形;
颜色不存在依赖属性;
形状的依赖属性为大小,且属性取值为圆形时依赖大小为大;
解决3:属性依赖
则先验概率 P(c) ,
P(c = 好果)= (4+1) / (10+2) = 5/12
P(c = 一般) = (6+1) / (10+2) = 7/12
带有依赖属性的类条件概率:
P(大小=大 | c=好果,形状=圆形) = (2+1)/(3+2) = 3/5
P(颜色=青色 | c=好果) = (0+1)/(4+2) = 1/6
P(形状=圆形 | c=好果,大小=大) = (2+1) / (3+2) = 3/5
P(大小=大 | c=一般,形状=圆形) = (1+1) /( 2+2) = 2/4
P(颜色=青色 | c=一般) = (5+1)/(6+2) = 6/8
P(形状=圆形 | c=一般,大小=大) = (1+1)/(3+2) = 2/5
因此:
P(c=好果) * P(大小=大 | c=好果,形状=圆形) * P(颜色=青色 | c=好果) * P(形状=圆形 | c=好果,大小=大)
= 5/12 * 3/5 * 1/6 * 3/5
= 0.025
P(c=一般) * P(大小=大 | c=一般,形状=圆形) * P(颜色=红色 | c=一般) * P(形状=圆形 | c=一般,大小=大)
= 7/12 * 2/4 * 6/8 * 2/5
= 0.0875
因此,测试集上要预测的这个样本和朴素贝叶斯分类器要预测的结果是相同的,都为一般的果子。
这种依赖属性选取算法称为超父ODE算法:SPODE。显然,这个算法是每个属性值只与其他唯一 一个有依赖关系。
基于它之上,又提出另一种基于集成学习机制,更为强大的独依赖分类器,AODE。
AODE算法
这个算法思路就是在SPODE算法的基础上在外面包一个循环,就是尝试将每个属性作为超父属性来构建SPODE:
上面的求和符号实质兑换为代码就是一个for循环吗。
总结:(半)朴素贝叶斯分类器,都有一个共同特点:假设训练样本所有属性变量的值都已被观测到,训练样本是完整的。
----------------------------------------------------------------------------------------------朴素贝叶斯算法:http://www.jianshu.com/p/94ec02bcd663
项目案例1: 屏蔽社区留言板的侮辱性言论项目案例2: 使用朴素贝叶斯过滤垃圾邮件项目案例3: 使用朴素贝叶斯分类器从个人广告中获取区域倾向
算法实现python:http://www.jianshu.com/p/163fe8eba7d9
算法实现Sklearn:http://www.jianshu.com/p/8bddc16c2db7
算法实现文本分类:http://www.jianshu.com/p/b8e0ae7cfa39
算法实现新浪新闻分类:http://mp.weixin.qq.com/s/Ty46-s0kvr2MpbUhQPXJfQ
----------------------------------------------------------------------------------------------