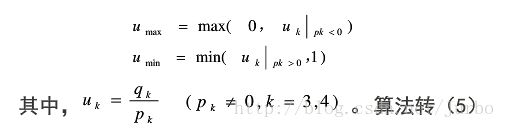计算机图形学 学习笔记（四）：直线裁剪算法：Cohen-Suther land，中点分割法，Liang-Barsky
接上文 计算机图形学 学习笔记（三）：多边形的区域填充算法，反走样算法
光栅图形学算法
本文主要讲解直线裁剪算法。
裁剪
使用计算机处理图形信息时，计算机内部存储的图形往往比较大，而屏幕显示的知识图形的一部分。因此需要确定图形哪些部分落在显示区内，哪些落在显示区外。这个选择的过程就称为裁剪。
最简单的裁剪方法是把各种图形扫描转换为点之后，再判断点是否在窗口内。
1、点的裁剪
但判断图形中每个点是否在窗口内，太费时，一般不可取。为提高效率，提出直线段的裁剪。
2、直线段的裁剪
直线段裁剪算法是复杂图形裁剪的基础。
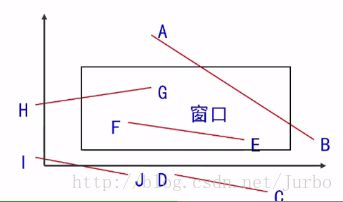
直线段和裁剪窗口的可能关系（如下图所示）：
- 完全落在窗口内
- 完全落在窗口外
- 与窗口边界相交
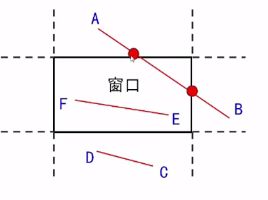
要裁剪一条直线段，首先要判断（如下图所示）：
- 它是否完全落在裁剪窗口内？
- 它是否完全在窗口外？
- 如果不满足以上两个条件，则计算它与一个或多个裁剪边界的交点（比如线段AB）。
常用的裁剪算法由三种，即 Cohen-Suther land、中点分割法、Liang-Barsky 裁剪算法。
3.1 直线裁剪算法：Cohen-Suther land（编码裁剪算法）
本算法又称为编码裁剪算法。
算法的基本思想是对每条直线段分三种情况处理：
（1）若点p1和p2完全在裁剪窗口内，则保留该直线
（2）若点p1（x1,y1）和 p2( x2,y2 ) 均在窗口外，且满足下列四个条件之一，就可以舍弃这条直线了：
（3）如果直线段既不满足保留的条件，也不满足舍弃的条件？那么需要对直线段按交点进行分段，分段后判断直线是保留还是舍弃。（大部分直线都是这种情况）
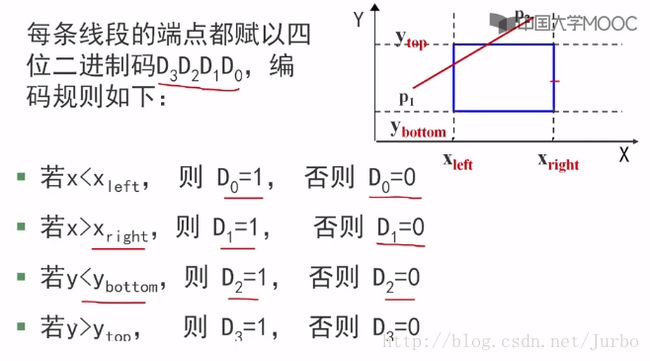
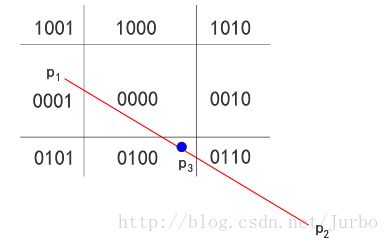
对于上述第三种情况，则每条线段的端点都应该赋以4位二进制编码。编码规则如图所示：
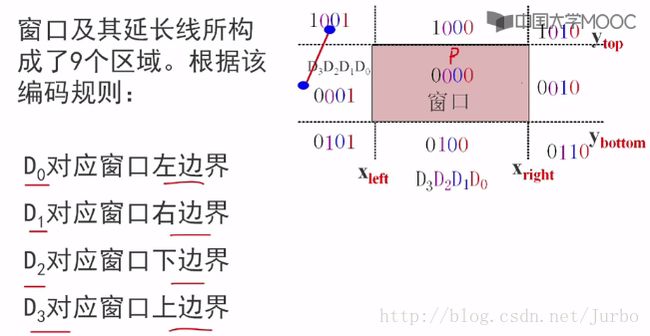
窗口与其延长线所构成了9个区域。编码如下：
在裁剪一条线段时，先求出端点 p1 和 p2 的编码 code1 和 code2,，然后进行二进制的“或”运算和“与”运算。再根据运算结果，判断线段是否保留
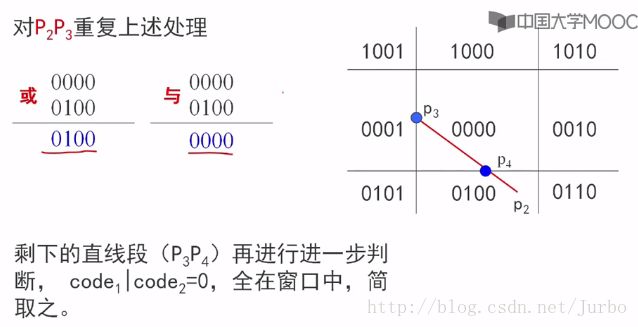
- 若 code1 | code2 =0 ，则保留此直线段
- 若 code1 & code2 !=0 ，则舍弃该线段
- 若上述两个两条均不成立，则需求出直线段与窗口边界的交点。再在交点处把线段一分为二，再进行处理（求出端点的编码后再进行二进制运算）
例子
小结
Cohen-Suther land 算法用编码的方法实现了对直线段的裁剪，比较适合两种情况：一是大部分线段完全可见，而是大部分线段完全不可见。
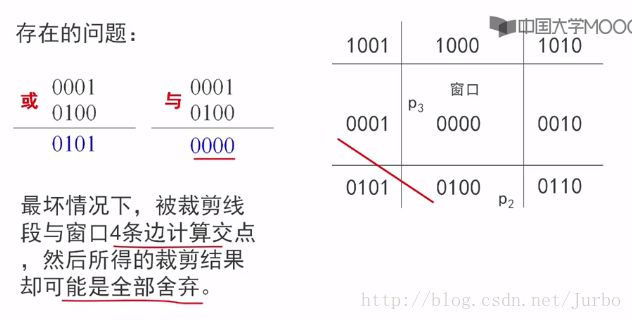
Cohen-Suther land 算法存在的问题：
3.2 直线裁剪算法：中点分割法
算法思想：和上面讲到的Cohen-Suther land 算法一样，首先对直线段的端点进行编码。
把线段和窗口的关系分成三种情况（和Cohen-Suther land 算法 差不多）：
- 完全在窗口内
- 完全在窗口外
- 和窗口有交点
中点分割算法的核心思想是通过二分逼近（不停的求中点）来确定直线段与窗口的交点。
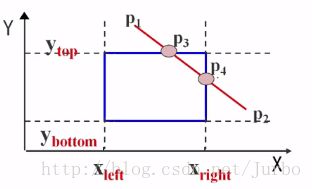
例子：比如求P1P2线段。P3是她们的中点。
P3和P2不在图形内，然后再舍弃，再找中点
注意：
1、若中点不在窗口内，则把中点和离窗口边界最远点构成的线段丢掉，以线段上的另一点和该中点再构成线段，再来求中点
2、如中点在窗口内，则又以中点和最远点构成线段，并求其中点，知道中点与窗口边界的坐标值在规定的误差范围内相等
3.3 直线裁剪算法：Liang-Barsky 裁剪算法（梁-Barsky算法）
在 Cohen-Suther land 算法提出后，梁友栋和Barsky 又针对标准矩形窗口提出了更快的 Liang-Barsky 裁剪算法。
梁算法的主要思想
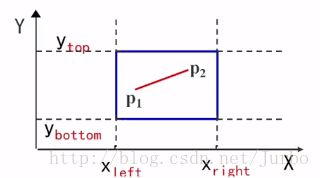
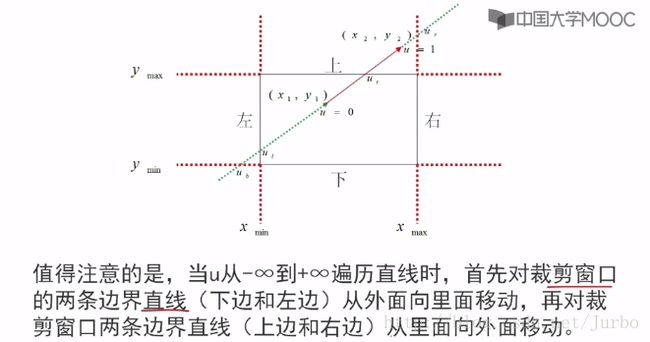
（1）对于一条直线段，之前讲的 DDA 或者 中点算法，我们对于直线段都是采用斜截式，一般式地方程。而 Liang-Barsky 采用用参数方程表示一条直线。
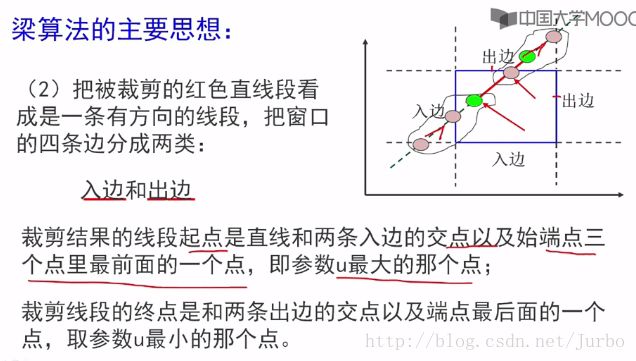
（2）把被裁剪的红色直线段看成是一条有方向的线段，把窗口的四条边分成两类：入边和出边。
需要注意：
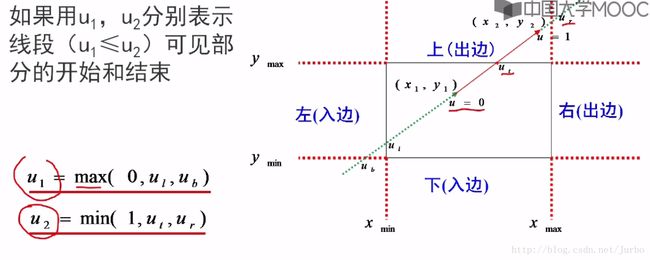
Liang-Barsky 裁剪算法步骤
例子
Liang-Barsky 算法小结
Cohen-Suther land 和 Liang-Barsky 裁剪算法 的比较
1、Cohen-Suther land 算法的核心思想是编码
2、如果被裁剪的图形大部分线段要么在窗口内或者要么完全在窗口外，很少有贯穿窗口的，那么Cohen-Suther land 算法的效果将非常好。
3、在一般情况下，Liang-Barsky 裁剪算法的效率优于 Cohen-Suther land 算法。