Matlab 快速入门

介绍 Matlab 的下载与安装，作图功能，线性代数，Matlab 程序设计相关内容。

---

下载与安装

http://blog.csdn.net/jurbo/article/details/78159201

注：Matlab 版本不同的话，除了界面有区别，该笔记仍然适用。

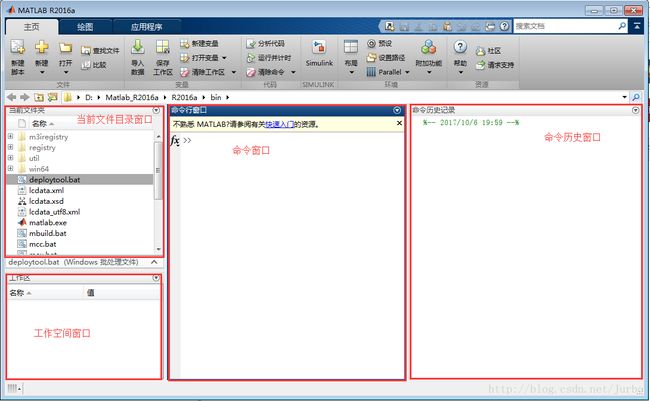
界面

Matlab 界面上主要有四个窗口，分别是：

1. 当前文件目录窗口（Current Folder）：位于左边，和“我的电脑”中的“资源管理器”很像，从这里可以直接转到目标文件所在的目录，用鼠标左键选中文件，再鼠标右击选择打开，则可以打开编辑或者运行它。

2. 命令窗口（Command Window）：最重要的窗口，提供交互式命令输入与输出的环境。在这里输入要执行的命令，则会在此窗口看到输出的数字结果或文字信息，而图形将会创建另外的图形窗口被输出。

3. 工作空间窗口（Workspace）：用于显示、编辑所有的变量，双击相关变量能自动打开。

4. 命令历史窗口（Command History）：记录用户曾经在 Matlab 中运行过的命令。

清理窗口信息的命令

1. clc：清除命令窗口内的内容，即只清扫屏幕，但不清除内存中已存在的变量
2. clf：擦除 Matlab 的当前图形窗口中的图形
3. clear：清除内存中的指定变量或函数
4. clear all：清除内存中所有的变量和函数

变量和数组

在 Matlab 中，可以用赋值的方式直接定义变量和数组，数组是以矩阵形式存放的。

元素放在方括号 [ ] 里，每行中的元素用空格或逗号分隔，矩阵的行用分号或者回车分隔。

例：输入数组（矩阵）的方式

键入：A=[1,2,3;4,5,6;7,8,9;10,11,12]
回车后显示结果：
A= 1 2 3
   4 5 6
   7 8 9
   10 11 12

指令执行后，矩阵 A 被保存在 Matlab 的工作空间（Workspace）中，以备后用。如果用户不用 clear 指令清除它或对它重新定义，该矩阵会一直保存在工作空间中，直到 Matlab 被关闭为止。

常见的常量矩阵命令

1. zeros(m,n)：产生一个 m*n 零矩阵
2. zeros(n)：产生一个 n 阶零方阵
3. ones(m,n)：产生一个所有元素为 1 的 m*n 矩阵
4. ones(n)：产生一个所有元素为 1 的 n 阶方阵
5. eye(n)：产生一个 n 阶单位阵

通常，在使用矩阵之前，先采用 zeros 定义并预设该矩阵，然后在使用的时候再给元素赋予所需要的值

语句和常量

Matlab 采用表达式语句，用户输入语句由 Matlab 系统直接运行。

Matlab 语句有两种常见的形式：

1. 表达式
2. 变量=表达式

具体用法说明如下：

1. 表达式由算符函数变量名和数组构成
2. 在第一种形式中表达式被执行后，产生的结果将被自动赋给名为 ans 的变量，并显示在屏幕上，ans 是一个缺省变量名，它会被垢面类似的操作刷新。
3. 在第二种形式中等号右边的表达式是将运算结果赋给等号左边的变量，并显示在屏幕上。
4. 书写表达式时运算符号有“=,+,-,*,/”等，两侧允许有空格以增加可读性，但在复数或符号演算表达式中要尽量避免装饰性空格以防出错
5. 变量名和函数名以一个字母打头，后面最多可接19个字母或数字

Matlab 区别字母大小写。

语句后加分号

如果 Matlab 语句后没有分号，则该语句执行结果会立即在 command window 中显示；而若有分号，则执行结果不会显示（但本身是输出或显示的语句不会受影响）。这个技巧在 脚本文件中很重要。因为我们可能只在意最后结果，而不在意中间的结果。

已预定义的常量

1. eps：计算机的最小整数。
2. pi：圆周率π
3. inf 或 Inf：无穷大∞
4. NaN：不定量
5. i 或 j：虚数单位，但可以重新被定义为别的变量。（如果没有赋值就直接使用，则默认为是虚数单位）

数字运算符

表达式由下列运算符构成，优先顺序是：+（加法），-（减法），*（乘法），/（除法），^（乘幂）

例：运算的优先级

键入：x=2*pi/3+2^3/5-0.3e-3
回车后显示结果：
x=3.6941

函数

Matlab 中的函数，可以分为三类：

1. 内部函数
2. 系统附带各种工具箱中的 M 文件所提供的大量函数
3. 用户自定义的函数（函数文件）

例：计算

x=logz−−−−√

键入：
z=1233.344
x=sqrt(log(z))
回车后显示结果

函数文件

Matlab 的函数文件是另一种形式的 M 文件，每一个函数文件都定义一个函数。事实上，Matlab 提供的标准函数大部分都是由函数文件定义的。

函数文件由 function 语句引导，其一般格式为：

function 输出形参表=函数名输入形参表

其中函数名的命名规则与变量名相同。输入形参为函数的输入参数，输出形参为函数的输出参数，当输出形参多余 1个时，则应该用方括号括起来。

例：编写函数文件求 小于任意自然数 n 的 Fibonacci（斐波那契）数列各项。Fibonacci（斐波那契）数列定义如下：f(k)=1 （k=1,2），f(k)=f(k-1)+f(k-2) （k>2）

函数程序如下：

function f=myfib(n)  %用于求数列的函数文件
f=[1,1];
i=1;
while f(i)+f(i+1)i+2)=f(i)+f(i+1)
    i=i+1
end

将以上函数文件以文件名 myfib.m 保存。注意该文件目录要添加到 Matlab 文件列表中，然后才可以在 Matlab 命令窗口输入一下命令 myfib(2000) ，来求小于2000的 Fibonacci 数列的各项。

myfib(2000)

数据的输入输出

命令窗口的输入 input 函数：A=input(提示信息选项)

例如，用户想输入 A 矩阵，则可以如下：

A=input('输入矩阵A:')

如果在调用 input 函数时采用了 ‘s’ 选项，则允许用户输入一个字符串。

例如，想输入一个人的姓名如下：

YourName=input('你的名字叫：','s')

例：求一元二次方程 ax^2+bx+c=0 的根。程序如下：

a=input('a=?');
b=input('b=?');
c=input('c=?');
d=b*b-4*a*c;
x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]

第一次运行：
a=?2
b=?6
c=?1
输出结果为：
x= -0.1771,-2.8229

第二次运行：
a=?4
b=?1
c=?4
输出结果为：
x=-0.1250+0.9922i,-0.1250-0.9922i

命令窗口的输出函数 disp（display）：disp(输出项）

其中，输出项既可以为字符串也可以为矩阵。

例：输出的例子

A=[1,2,3;4,5,6;7,8,9];
disp(A)
输出为：
      1 2 3
      4 5 6
      7 8 9

关系及逻辑运算

在执行关系及逻辑运算时，Matlab 将输入的不为零的数值都视为真（true），而为零的数值则视为假（false），运算的输出值将判断为真以 1 表示，反之则为 0 表示假。

关系运算符有：

1. <：小于
2. <=：小于等于
3. >：大于
4. >=：大于等于
5. ==：等于
6. ~=：不等于
7. &&：逻辑与 and
8. |：逻辑或 or
9. ~：逻辑非 not

上述的各个关系运算符既可以用于数也可以用于矩阵。

选择结构

选择结构是根据给定的条件，成立或不成立，分别执行不同的语句。

Matlab 提供的用于实现选择结构的语句，有 if 语句和 switch 语句。

在 Matlab 中，if 语句有3种格式，如下所示

格式1：
    if 条件
        语句组
    end

格式2：
    if 条件
        语句组1
    else
        语句组2
    end

格式3：
    if 条件1
        语句组1
    elseif 条件2
        语句组2
    .....
    elseif 条件m
        语句组m
    else
        语句组m+1
    end

switch 语句：switch 语句根据变量或表达式的取值不同，分别执行不同的语句。格式如下：

switch 表达式
    case 值1
        语句组1
    case 值2
        语句组2
    ....
    case 值m
        语句组m
    otherwise %其他值
        语句组m+1
end     

循环结构

循环是指按照给定的条件重复执行指定的语句。Matlab 提供了两种实现循环结构的语句：for 语句和 while 语句。

for 语句格式：

for 循环变量=表达式1：表达式2：表达式3
    循环体语句
end

表达式1 的值是循环变量的初值，表达式2 的值是循环变量的增量，表达式3 的值为循环变量的终值。如果增量为1 时，表达式2 可以省略不写。

例：给出公式 y=1+1/3+1/5+….+1/(2n-1)，求当n=100时的 y 值。

y=0;
n=100;
for i=1:n
    y=y+1/(2*i-1);
end
display(y)

输出为：y=3.2843

while 语句的一般格式为：

while 条件
    循环体语句
end

帮助系统

遇到一个命令或者函数，不清楚用法时，可以在菜单上选择打开帮助手册，按照分类查询或者搜索这个关键词。也可以在命令窗口直接键入命令

help 函数名或命令名

线性代数

Matlab 最擅长于线性代数中关于矩阵的各种运算，常用的运算符有：

1. +：两矩阵和的运算
2. -：两矩阵减的运算
3. *：两矩阵乘积的运算
4. .*：两矩阵各相应位置元素乘积的运算
5. ./：两矩阵各相应位置元素相除的运算
6. A’：矩阵 A 的转置
7. inv（A）：矩阵 A 的逆阵
8. eig（A）：矩阵 A 的特征值
9. [V,D]=eig（A）：给出由矩阵 A 的特征向量组成的矩阵 V（以列向量排列）和由对应的特征值组成的对角阵 D（特征值为对角线元素）
10. sum（A,1）：对矩阵 A 的每列元素求和，给出求和值的行向量
11. sum（A,2）：对矩阵 A 的每行元素求和，给出求和值的列向量
12. sum（X）：对向量 X=（x1,x2,…….,xn）的分量求和
13. cumsum（X）：给出向量 X 的累加和
14. length（X）：给出向量 X 的维数，即其分量的个数
15. norm（X）：给出向量 X 的范数，即向量的长度

例：求线性方程组 AX=B 的解

A=[3 2 1;2 6 4;1 4 8]; B=[1 1 1]';
X=inv(A)*B
输出的解：
X=0.2973
  0.0135
  0.0811

上面的解也可以采用运算符“\”给出：X=A\B

例：求矩阵的特征值与相应的特征向量

A=[3 2 1;2 6 4;1 4 8];  [V,D]=eig(A)
输出结果为：
V=0.7516 0.6179 0.2311
 -0.6037 0.5029 0.6186
  0.2660 -0.6044 0.7509
D=1.7475 0       0
  0      3.6496  0
  0      0       11.6029

作图功能

Matlab 具有很强的图形处理能力。

二维图形

Matlab 中最常用的绘图函数为 plot，根据不同的坐标参数它可以在二维平面上绘制出不同的曲线。类似地，在三维空间里绘图函数是 plot3。

plot 函数

plot 函数调用格式：plot(x,y)

其中 x 和 y 为坐标向量，函数功能以向量 x 作为 X轴，以向量 y 作为 Y轴绘制二维X-Y 曲线。需要注意：向量 x 和 y 的长度必须相等，否则将出错。

例：在区间 [0,2π] 内绘制正弦曲线 y=sinx 的语句

x=0:pi/100:2*pi;
y=sin(x);
plot(x,y)

指定线型与颜色

指定绘图线型与颜色的命令格式是：

plot(x,y1,'cs1',x,y2,'cs2',....)

它以公共向量 x 为 X 轴，分别以 y1,y2，… 为 Y 轴在同一幅图内绘制出多条曲线，同时可以指定它们的不同颜色与不同线性。

每条曲线的颜色和线型用字符串 ‘cs’ 来指定，其中 c 表示颜色，而 s 表示线型，线型可以是线或者标记，线和标记可同时使用。它们的位置次序可随意，如缺省的话，则默认颜色为蓝色、线型为实型。它们的符号如下所示。

颜色符号	颜色符号说明	标记与线型符号	符号说明
y	黄色	o	圆圈标记
m	黄色	s	方形标记
c	青色	^	三角形标记
r	红色	x	叉号标记
g	绿色	-	实线
b	蓝色	-.	点划线
w	白色	:	点线
k	黑色	_	虚线

另外，可以用 plot(x,y,’linewidth’,n) 来指定线宽为 n 磅

例：在区间 [0,2π] 内同时绘制不同线型、不同颜色的正弦曲线 y=sin(x) 和余弦函数 y=cos(x) 的语句

x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'b-',x,y2,'k:')

图形的文字标注

可以对图形加上一些文字说明的标注，如图形名称、图形某一部分的含义坐标。

例：图形的文字标识方式

x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k-',x,y2,'k:');
title('sin 和 cos 曲线')
xlabel('自变量x')
ylabel('因变量y')
text(2.8,0.5,'sin(x)')
text(1.4,0.3,'cos(x)')

设定坐标轴

在绘制图形时，系统自动给出图形的坐标轴，用户也可以利用 axis 函数对其重新设定。

axus 的功能如下：

1. axis([xmin,xmax,ymin,ymax])：设定坐标轴的最大值和最小值
2. axis auto：将坐标系统返回自动缺省状态
3. axis square：将当前图形设置为方形，系统默认为矩形
4. axis equal：两个坐标因子设定成相等
5. axis tight：将坐标轴限定在数据的范围内
6. axis off：关闭坐标系统
7. axis on：显示坐标系统

例：在坐标范围 0<=x<=2π，-1<=y<=2 内绘制正弦曲线

x=linspace(0,2*pi); 
y=sin(x);
plot(x,y)
axis([0,2*pi,-1,2])  %设定坐标范围

添加图例

例：在图形中添加图例的例子

x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k-',x,y2,'k:')
title('sin 和 cos 曲线')
xlabel('自变量x')
ylabel('因变量y')
text(2.8,0.5,'sin(x)')
text(1.4,0.3,'cos(x)')
legend('sin(x)','cos(x)')

subplot 绘制多个子图

subplot 函数是在一幅图中绘制多个子图的命令，其格式是：subplot(m,n,k)

在一副图中共绘制 m*n 个子图，它们以 m 行、n 列的阵列格式排列，这里 k 是指定绘制其中第 k 个子图（编号按行以此排序），要配合 plot 命令一起使用。

例：画子图的命令 subplot(m,n,p) 示例

x=linspace(0,2*pi,60);
y=sin(x);
z=cos(x);
t=sin(x)./(cos(x)+eps);
ct=cos(x)./(sin(x)+eps);
subplot(2,2,1)
plot(x,y)
title('sin(x)')
axis([0,2*pi,-1,1])
subplot(2,2,2)
plot(x,z)
title('cos(x)')
axis([0,2*pi,-1,1])
subplot(2,2,3)
plot(x,2)
title('tangent(x)')
axis([0,2*pi,-40,40])
subplot(2,2,4)
plot(x,ct)
title('cotangent(x)')
axis([0,2*pi,-40,40])

hold 命令，在原图形窗口继续画图

若在已存在的图形窗口中用 plot 函数继续添加新的图形内容，可使用图形保持指令 hold 命令：

• hold on：在它之后再执行 plot 函数，则可以在保持原有图形的基础上添加新的图形
• hold off：绘制好图形后用它来关闭添加功能

注意：如果忘了关闭，可能会把后面的的程序运行带来不可预料的结果。

例：使用 hold 命令在同一坐标框内绘制多条曲线的示例：

x=linspace(0,2*pi,60);
y=sin(x);
z=cos(x);
plot(x,y,'k-')
hold on
plot(x,z,'k:')
axis([0,2*pi,-1,1])
legend('sin(x)','cos(x)')
hold off

绘制自定义函数 f(x) 的曲线

函数格式：fplot(fname,lims,tol)

其中 fname 为函数名，以字符串形式出现，lims 为变量取值范围，tol 为相对允许误差。

例：为了绘制 f(x)=cos(tan(πx)) 曲线，可先建立函数文件 fct.m 如下：

function y=fct(x)
y=cos(tan(pi*x));

用 fplot 函数调用 fct.m 函数格式

fplot('fct',[0,1],1e-4,':')

特殊坐标图形

除了 plot 等基本绘图函数外，Matlab 系统还提供许多其他特殊绘图函数。

双对数坐标

采用双对数坐标系绘图的命令格式是：loglog：在双对数坐标系上绘制图形

例：函数 loglog(x,y) 用来绘制双对数坐标图

x=0:0.1:2*pi;
y=abs(1000*sin(4*x))+1;
loglog(x,y)

单对数坐标

采用单对数坐标系绘图的命令格式是：

• semilogx：在以 X 轴为对数的坐标系上绘制图形
• semilogy：在以 Y 轴为对数的坐标系上绘制图形

例：函数 semilogx(x,y) 用来绘制以 X 为对数坐标轴的图

x=0:0.01:2*pi
y=abs(1000*sin(4*x))+1;
semilogx(x,y)

同样以 Y 为对数坐标轴的图：

x=0:0.1:2*pi;
y=abs(1000*sin(4*x))+1;
semilogy(x,y)

阶梯图形

使用函数 stairs(x,y) 可绘制阶梯图形

例：绘制如下阶梯图形

x=-2.5:0.25:2.5;
y=exp(-x.*x);
stairs(x,y),grid on

在这里我们还使用了显示网格线的功能，其命令是 grid on，如果想要关闭则用 grid off

条形图形

函数 bar(x,y) 用来绘制条形图。

例：绘制如下条形图

x=-2.5:0.25:2.5;
y=exp(-x.*x);
bar(x,y)
title('条形图')

二维绘图函数小结

1. plot：绘制二维图形的函数
2. subplot：创建子图
3. fplot：f(x) 函数曲线绘制
4. fill：填充二维多边图形
5. bar：条形图
6. stairs：阶梯图形
7. hold on：打开添加图形功能的命令
8. hold off：关闭添加图形功能的命令
9. loglog：双对数坐标图
10. semilogx：X 轴为对数的坐标图
11. semilogy：Y 轴为对数的坐标图
12. text：放置文本
13. title：标注图形的文本标题
14. axis：设置坐标框大小
15. xlabel：放置 X轴坐标标记
16. ylabel：放置 Y轴坐标标记

三维图形

plot3 最基本的三维图形

最基本的三维图形函数为 plot3。它是将二维函数 plot的有关功能扩展到三维空间，用来绘制三维图形函数，除了增加了第三维坐标外，其他功能与二维函数 plot 相同。

调用格式：plot3(x1,y1,z1,’c1’,x2,t2,z2,’c2,…)

其中 x1,y1,z1…..表示三维坐标向量。’c1’,’c2’,表示线型或颜色。

例：绘制三维螺旋线

t=0:pi/50:10*pi;
y1=sin(t);
y2=cos(t);
plot3(y1,y2,t)
title('螺旋线'),text(0,0,0,'原点')
xlabel('sin(t)'),ylabel('cos(t)'),zlabel('t')
grid

mesh 三维网格图

mesh 函数用于绘制三维网格图，在不需要绘制特别精细的三维曲面结构时，可通过绘制三维网格图来表示三维曲面图。

三维曲面的网格图最突出的优点是它较好地解决了实验数据在三维空间的可视化问题。

函数调用格式：mesh(x,y,z,c)

其中，x,y 控制 X 和 Y 轴坐标，矩阵 z 是由（x,y）求得的 Z 轴坐标，x,y,z 组成了三维空间的网格点，而 c 是字符串变量，用于控制网格点的颜色。

例：绘制一个三维网格曲面图

x=0:0.15:2*pi;
y=0:0.15:2*pi;
z=sin(y')*cos(x);  %矩阵相乘
mesh(x,y,z)
title('三维网格图形')

surf 三维曲面图

surf 函数用于绘制三维曲面图，各线条之间的补面用颜色填充，其函数调用格式与 mesh 函数一样：surf(x,y,z)

其中 x,y 分别控制 X 和 Y 轴坐标，矩阵 z 是由（x,y）求得的曲面上 Z 轴坐标。

例：绘制三维曲面图语句：

x=0:0.15:2*pi;
y=0:0.15:2*pi;
z=sin(y')*cos(x);
surf(x,y,z)
title('三维曲面')

M 文件

Matlab 有两种工作方式，一种是交互式的命令行工作方式，另一种是 M 文件的脚本程序的工作方式。后者，Matlab 被当做一种高级编程语言为用户提供了二次开发的工具。

用 Matlab 语言编写的程序称为 M 脚本文件（简称 M 文件），M 文件有两类文件。分别是命令文件和函数文件。两者区别在于命令文件没有输入参数，也不返回输出参数，而函数文件可以输入参数，也可以返回参数。

建立新的 M 文件

M 文件可以用任何文本编辑程序建立和编辑（扩展名为 .m即可）。而一般最常用且最为方便的就是使用 Matlab 提供的 M 文件编辑器。

从 Matlab 命令窗口的 File 菜单中，选择 New 菜单项，再选择 M-file 命令将得到 M 文件窗口。在 M 文件窗口中输入 M 文件的呢日哦那个，输入完毕后选择此窗口 File 菜单的 save as 对话框，在对话框的 File 框中输入文件名，注意其扩展名必须为“.m”，再选择 OK 按钮即可以完成 M 文件的建立。

编辑已有的 M 文件

从 Matlab 命令窗口的 File 菜单中，选择 Open M-file 命令，则屏幕出现 Open 对话框。在 Open 对话框中的 File Name 框中输入文件名，必要时加入路径或从右边的 Directories 框中，打开这个 M 文件所在的目录；再从 File Name 下面的列表框中，选中这个文件，然后按 OK 按钮，即可打开这个 M文件。

在 M 文件窗口可以对打开的 M 文件进行编辑修改，在编辑完成后选择 File 菜单中的 Save 命令，可以把这个编辑过的 M 文件保存下来。