吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（3-1）-- 机器学习策略（1）

---

作者： 大树先生
博客： http://blog.csdn.net/koala_tree
知乎：https://www.zhihu.com/people/dashuxiansheng
GitHub：https://github.com/KoalaTree
2017 年 10 月 18 日

---

以下为在Coursera上吴恩达老师的DeepLearning.ai课程项目中，第三部分《结构化机器学习项目》第一周课程“机器学习策略（1）”关键点的笔记。本次笔记并没有涵盖所有视频课程的内容。在阅读以下笔记的同时，强烈建议学习吴恩达老师的视频课程，视频请至 Coursera 或者 网易云课堂。

---

同时我在知乎上开设了关于机器学习深度学习的专栏收录下面的笔记，方便在移动端的学习。欢迎关注我的知乎：大树先生。一起学习一起进步呀！^_^

---

结构化机器学习项目 — 机器学习策略（1）

1. 正交化

表示在机器学习模型建立的整个流程中，我们需要根据不同部分反映的问题，去做相应的调整，从而更加容易地判断出是在哪一个部分出现了问题，并做相应的解决措施。

正交化或正交性是一种系统设计属性，其确保修改算法的指令或部分不会对系统的其他部分产生或传播副作用。 相互独立地验证使得算法变得更简单，减少了测试和开发的时间。

当在监督学习模型中，以下的4个假设需要真实且是相互正交的：

• 系统在训练集上表现的好
  
  • 否则，使用更大的神经网络、更好的优化算法
• 系统在开发集上表现的好
  
  • 否则，使用正则化、更大的训练集
• 系统在测试集上表现的好
  
  • 否则，使用更大的开发集
• 在真实的系统环境中表现的好
  
  • 否则，修改开发测试集、修改代价函数

2. 单一数字评估指标

在训练机器学习模型的时候，无论是调整超参数，还是尝试更好的优化算法，为问题设置一个单一数字评估指标，可以更好更快的评估模型。

example1

下面是分别训练的两个分类器的Precision、Recall以及F1 score。

由上表可以看出，以Precision为指标，则分类器A的分类效果好；以Recall为指标，则分类器B的分类效果好。所以在有两个及以上判定指标的时候，我们很难决定出A好还是B好。

这里以Precision和Recall为基础，构成一个综合指标F1 Score，那么我们利用F1 Score便可以更容易的评判出分类器A的效果更好。

指标介绍：

在二分类问题中，通过预测我们得到下面的真实值 y 和预测值 y^ 的表：

• Precision（查准率）：
  
  Precision=True positiveNumber of predicted positive×100%=True positiveTrue positive+False positive
  
  假设在是否为猫的分类问题中，查准率代表：所有模型预测为猫的图片中，确实为猫的概率。
• Recall（查全率）：
  
  Recall=True positiveNumber of actually positive×100%=True positiveTrue positive+False negative
  
  假设在是否为猫的分类问题中，查全率代表：真实为猫的图片中，预测正确的概率。
• F1 Score：
  
  F1−Socre=21p+1r
  
  相当与查准率和查全率的一个特别形式的平均指标。

example2

下面是另外一个问题多种分类器在不同的国家中的分类错误率结果：

模型在各个地区有不同的表现，这里用地区的平均值来对模型效果进行评估，转换为单一数字评估指标，就可以很容易的得出表现最好的模型。

3. 满足和优化指标

假设有三个不同的分类器性能表现如下：

又时对于某一问题，对模型的效果有一定的要求，如要求模型准确率尽可能的高，运行时间在 100 ms 以内。这里以Accuracy为优化指标，以Running time为满足指标，我们可以从中选出B是满足条件的最好的分类器。

一般的，如果要考虑N个指标，则选择一个指标为优化指标，其他N-1个指标都是满足指标：

Nmetric:{1Optimizing metricNmetric−1Satisificing metric

4. 训练、开发、测试集

训练、开发、测试集选择设置的一些规则和意见：

• 训练、开发、测试集的设置会对产品带来非常大的影响；
• 在选择开发集和测试集时要使二者来自同一分布，且从所有数据中随机选取；
• 所选择的开发集和测试集中的数据，要与未来想要或者能够得到的数据类似，即模型数据和未来数据要具有相似性；
• 设置的测试集只要足够大，使其能够在过拟合的系统中给出高方差的结果就可以，也许10000左右的数目足够；
• 设置开发集只要足够使其能够检测不同算法、不同模型之间的优劣差异就可以，百万大数据中 1% 的大小就足够；

5. 改变开发、测试集和评估指标

在针对某一问题我们设置开发集和评估指标后，这就像把目标定在某个位置，后面的过程就聚焦在该位置上。但有时候在这个项目的过程中，可能会发现目标的位置设置错了，所以要移动改变我们的目标。

example1

假设有两个猫的图片的分类器：

• 评估指标：分类错误率
• 算法A： 3% 错误率
• 算法B： 5% 错误率

这样来看，算法A的表现更好。但是在实际的测试中，算法A可能因为某些原因，将很多色情图片分类成了猫。所以当我们在线上部署的时候，算法A会给爱猫人士推送更多更准确的猫的图片（因为其误差率只有 3% ），但同时也会给用户推送一些色情图片，这是不能忍受的。所以，虽然算法A的错误率很低，但是它却不是一个好的算法。

这个时候我们就需要改变开发集、测试集或者评估指标。

假设开始我们的评估指标如下：

Error=1mdev∑i=1mdevI{y(i)pred≠y(i)}

该评估指标对色情图片和非色情图片一视同仁，但是我们希望，分类器不会错误将色情图片标记为猫。

修改的方法，在其中加入权重 w(i) ：

Error=1∑w(i)∑i=1mdevw(i)I{y(i)pred≠y(i)}

其中：

w(i)={1如果x(i)不是色情图片10或100如果x(i)是色情图片

这样通过设置权重，当算法将色情图片分类为猫时，误差项会快速变大。

总结来说就是：如果评估指标无法正确评估算法的排名，则需要重新定义一个新的评估指标。

example2

同样针对example1中的两个不同的猫图片的分类器A和B。

但实际情况是对，我们一直使用的是网上下载的高质量的图片进行训练；而当部署到手机上时，由于图片的清晰度及拍照水平的原因，当实际测试算法时，会发现算法B的表现其实更好。

如果在训练开发测试的过程中得到的模型效果比较好，但是在实际应用中自己所真正关心的问题效果却不好的时候，就需要改变开发、测试集或者评估指标。

Guideline：

1. 定义正确的评估指标来更好的给分类器的好坏进行排序；
2. 优化评估指标。

6. 与人类表现做比较

可避免偏差

假设针对两个问题分别具有相同的训练误差和交叉验证误差，如下所示：

对于左边的问题，人类的误差为 1% ，对于右边的问题，人类的误差为 7.5% 。

对于某些任务如计算机视觉上，人类能够做到的水平和贝叶斯误差相差不远。（这里贝叶斯误差指最好的分类器的分类误差，也就是说没有分类器可以做到 100% 正确）。这里将人类水平误差近似为贝叶斯误差。

• 左边的例子： 8% 与 1% 差距较大
  主要着手减少偏差，即减少训练集误差和人类水平误差之间的差距，来提高模型性能。
• 右边的例子： 8% 与 7.5% 接近
  主要着手减少方差，即减少开发集误差和测试集误差之间的差距，来提高模型性能。

理解人类表现

如医学图像分类问题上，假设有下面几种分类的水平：

1. 普通人： 3% error
2. 普通医生： 1% error
3. 专家： 0.7% error
4. 专家团队： 0.5% error

在减小误诊率的背景下，人类水平误差在这种情形下应定义为： 0.5% error；

如果在为了部署系统或者做研究分析的背景下，也许超过一名普通医生即可，即人类水平误差在这种情形下应定义为： 1% error；

总结：

对人类水平误差有一个大概的估计，可以让我们去估计贝叶斯误差，这样可以让我们更快的做出决定：减少偏差还是减少方差。

而这个决策技巧通常都很有效果，直到系统的性能开始超越人类，那么我们对贝叶斯误差的估计就不再准确了，再从减少偏差和减少方差方面提升系统性能就会比较困难了。

7. 改善模型的表现

基本假设：

• 模型在训练集上有很好的表现；
• 模型推广到开发和测试集啥会给你也有很好的表现。

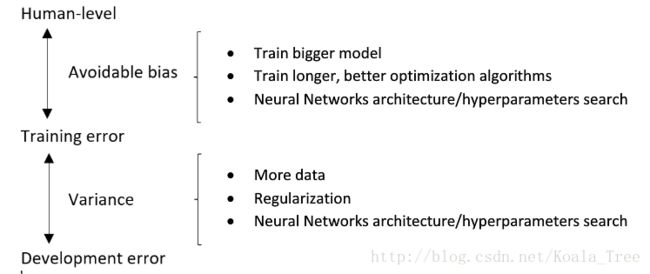
减少可避免偏差

• 训练更大的模型
• 训练更长时间、训练更好的优化算法（Momentum、RMSprop、Adam）
• 寻找更好的网络架构（RNN、CNN）、寻找更好的超参数

减少方差

• 收集更多的数据
• 正则化（L2、dropout、数据增强）
• 寻找更好的网络架构（RNN、CNN）、寻找更好的超参数