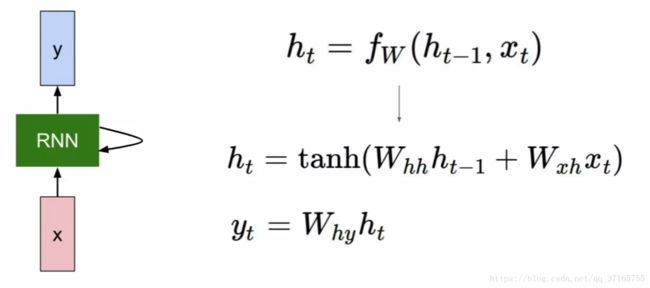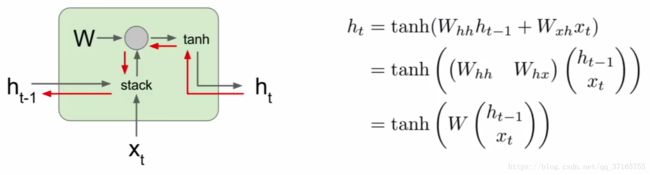卷积神经网络 + 机器视觉: L10_RNN_LSTM (斯坦福CS231n)
完整的视频课堂链接如下:
- https://www.youtube.com/watch?v=6niqTuYFZLQ&index=10&list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv
完整的视频课堂投影片连接:
- http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture10.pdf
前一課堂筆記連結:
- 卷积神经网络 + 机器视觉:L9_VGG_GoogleNet_ResNet (斯坦福课堂)
RNN 是一个包含非常广泛的应用领域与知识范围的一大门类,他的全名又叫做 Recurrent Neural Network,也是神经网络的一种,但是差别就在于 RNN 让神经网络中的节点(node)在运算的时候,还参考了“历史信息”,能够见往知来的贯通所有节点的讯息,并通过新数据与历史数据的彼此关系和出现顺序来预测下一个 output 的结果。
虽然上述说得轻描淡写,但是为了达到以上效果,有许多架构与方法必须被套用到其中,很多内容超出了 Stanford CNN 课程的范畴,我一并整理在了下文,后续持续开新篇幅针对介绍。历史信息与序列的先后引发的延伸应用是一种不同维度的跃进过程,但凡有先后性的资料,都可以跟 RNN 拉上关系,例如:文字,影片,声音,甚至是股票信息。
文字又包含了描述语句,新闻搞,论文,摘要,评论分析,书面翻译等等数不清的分项应用。影片类似道理也包含了物件互动关系,行为意义,肢体语言等。声音则像是语音识别,语义识别,语音翻译等。如果这三大类做 C3取 2 的排列组合,那还有一堆梦幻般的应用场景值得挖掘。
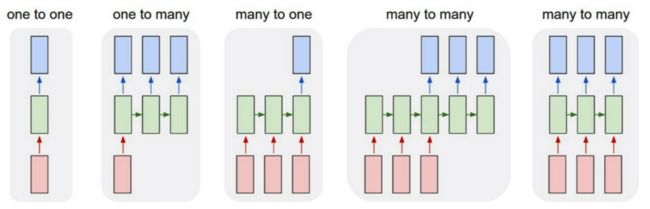
RNN 运行顺序 (Process Sequences)
上图中一共有 4 种 case,按照顺序说下来的用法即为:
- Vanilla Neural Networks,一进一出(最简单的形式)
- Image Captioning,一进多出(给一张图,用文字描述内容)
- Sentiment Classification & Video Recognition,多进一出(连续动作判断行为归属)
- Machine Translation between Languages,多进多出(翻译工作)
Introduction paper link: Connectionist Temporal Classification (CTC)
加上历史信息这个维度带给我们的优势是不可言喻的,时间串起了世界的运转走向,很多事务只有时间维度的参与,其本质与意义才能够被赋予,RNN 最大的优势莫过于此,综合了庞大的电脑运算能力与数据资料,让多个维度的考量成为了可能。
2014 年底新提出的一篇论文 Neural Turing Machine,可以把 model 自己新学到的东西放入到 Machine's Memory 里面做新一轮的迭代。
The Composition of Modern RNN
- Input data
- Hidden RNN layers
- Memory functionality
- Selecting logic
- Output data
这个架构又叫做 LSTM 的架构,因为最简单的 RNN model 在作为深层的神经网络的时候是有许多问题存在的,为了解决问题并且同时保有原本的 RNN 效能,LSTM 因应而生,这个 model 也因此已经成为了 RNN 的代名词,基本上没有人在用最简单的 RNN model 去训练数据了。
但是为了透彻理解 RNN 原理,还是必须回顾到最简单的 model 上,一步一步的一窥究竟。一进一出的 case 种,公式如下:
代数说明:
t - 表示位于 t 的时间点,t-1 就是上一个单位的时间点
h - 表示 hidden layer 的内部运行机制
W - 表示权重,后面跟着两个小代数先表明哪个参数的,再表明哪个方程的
x - 表示 input data
y - 表示 output data
把当下的 x 还有上一次运算好的 hidden layer 里面的结果作为两个 input 代入新的 hidden layer 里面,这个 hidden layer 里面的机制是个 tanh function,运算出来后再乘上一个 W 作为 output 输出,这么一来就把历史信息也一并考虑进去了。如果把这个机制作为一个 unit 把很多歌同样的 unit 串起来,结果就会是如下图:
可以看出来 W 是一个回收再利用的参数不断的被重新放入下一个时间点的 unit 里面,并且同样的 W 在 RNN 里面也是要被训练的,每次 output 出来后会根据标准数据得出一个 loss value,同样藉由 Gradient Descent 还有 Backpropagation 的方法,把 loss 值降到最低,逼出最优状态。为了提升准确率,RNN 甚至可以是双向的过程,又称为 bidirectional RNN。真正意义上做到 “鉴往知来” 的境界。
RNN 的架構其实有两个些微不同的版本,分别叫做 Elman 和 Jordan Network,差别就在于历史信息的储存方式不同,Elman 是把 hidden layer 的结果作为下一层 network 的输入迭代,反观 Jordan 则是把整个 unit 的 layer 输出作为下一个 unit 的输入,就结果而言其实差异不大。
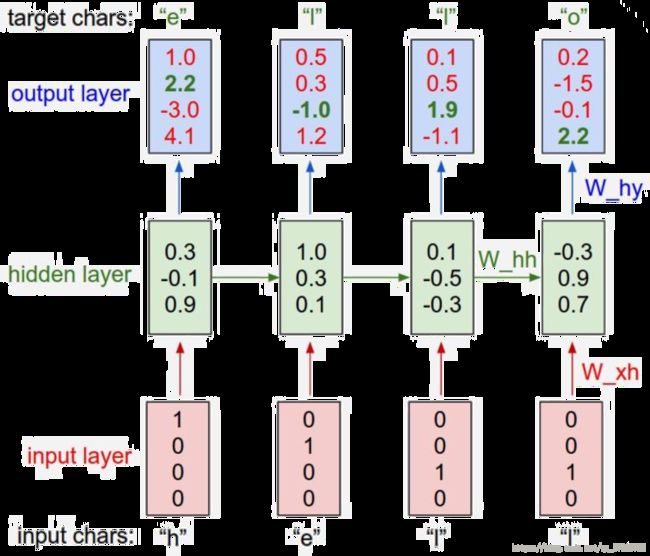
用 RNN model 测试简单的 文字顺序问题的话,实际案例如下:
如果希望 RNN 能够拼出 “hello” 这个字,那么我们就要设计每个字母后面出现下一个字母的可能性有多少,例如上例中,h 后面出现 e 的可能只有 2.2, 但是出现 o 的可能却是 4.1,显然是一个不合格的状态,因此经过 loss function 得出来的值应该会很大,需要继续使用 GD 去优化参数,并使得最后结果能够尽可能地贴近我们的预期。
RNN Gradient Flow
梯度流可视化过程与对应的共识如下:
先是一个数据和历史信息与 W 的 dot product 过程,再把结果放到 tanh 里面加工,得出一个 output,dot 的微分做起来相对轻松,但是 tanh 就不是那么好说话的角色了,占用资源的 tanh 和会消失或爆炸的 W 使得这个 model 有无尽的瓶颈。
暂时的方法:Gradient Clipping,代码如下:
grad_norm = np.sum(grad * grad)
if grad_norm > threshold:
grad *= (threshold / grad_norm)
用一个判断式阻断梯度通往爆炸或是消失的途径,但是斩草不除根的情况下这个方法还是被诟病的。这个初阶的 model 有着无可避免的痛点,随着神经网络的深度增加,劣势暴露的更加明显,有两个原因导致初阶版本的神经网络瘫痪:
- tanh 的反向传播计算是个占用资源的过程,tanh 中的 tanh 中的 tanh... 循环下去的微分更是一个庞大的计算负担
- 梯度爆炸或是消失 Gradient Exploding or Vanishing,这里不像 CNN 里面有 Batch Normalization 等缓解此症状的机制,在传递误差的时候更无可能不断延伸,即便 W 是 1.1 到后来也是爆炸收场,0.9 也是消失结束
tanh 在使用上更为符合我们的预期,效果也更好,作为一个 activation function 的存在是不可被替代的,而 BN 是用在 data 上的方法,也不是直接套用在 W 上的,在这两个问题没办法被侧面绕开的情况下,聪明的人脑还是想出了因应之道。
Truncated Backpropagation
第一招就是减负。随着深度增加,运算量成了负担,因此我们就选择只 BP 到一定的深度即可,如要计算第 100 层的梯度,就选前 50 层去做 BP 然后剩下的部分就不管了,同理其他层节点的梯度运算,这个方式类似 Mini-Batch 的逻辑,可以大幅减少计算成本,从经济效益来看,损失一些精确度换来时间,非常划算。
第二招就是重构整个 model,也就是 LSTM 诞生的原因,介绍前先更深入的理解 simple model 出问题的症结点。
Long Short-Term Memory (LSTM)
这个方法早在 1997 年就已经被发明使用,它把原本简单的 model 内容增加了更多东西,如最一开始介绍的 RNN 结构,含有记忆门,遗忘门,选择门等通道,更加细致的过滤问题。不过这个章节中 Stanford 课说的并不够完整和易懂,两篇补充文章值得一读:理解 LSTM 网络(点击) & RNN 及 LSTM 的介绍和公式梳理(点击)。
并且仔细上了一位台湾大学教授李宏毅的线上课程 part1 与 part2 后,终于能够初步完整的继续撰写此文,顺利为我填补了 Stanford 留下来的知识空缺(发自内心的感谢大神老师)。顾名思义,其实它就是一个 “长了一点” 的短期记忆算法架构,拥有多个掌管不同部位的 Gate 去控制数据的 “流” ,经过 Gate 的筛选,让有意义的 data 被留下,而是否有意义这件事情,则是 machine learning 重要的一环。(这些图片中也使用到了李老师提供的 PPT,只为更好的诠释内容)
图像中建构好了架构后,接下来就是把架构数学化,最后再把数学转换成电脑可执行的代码,等看到结果符合预期当下,最激动人心的刹那莫过于此了! Gate 无非就是一个 “是与否” 的判断,使用 Sigmoid function 非常恰当。LSTM 的组成有: input gate, forget gate, output gate, Memory cell 四个部分。
有别于前面几节课记录的内容,一般 Neural Network 的 input 只有一个对应的处理通道,那就是乘以 Weight 加上 bias 之后把结果塞进 activation function 里面得到一个神经 unit 的输出结果,并以此结果作为下一层神经 unit 的 input 不断迭代。然而对于 RNN 的 LSTM model 而言,input data 却需要塞到到四个对应不同权重 Weights 的通道之中作为信息源,提供个别通道的学习方向,这四个通道分别是:input data, input gate, forget gate, output gate。
如上流程图,所有的 Gates 都是一种 activation function 参与,以下分别说明:
- input data, position of z
首先用同一个 fed in data 乘以属于这个 gate 专属的 Weight,再加上属于这个 gate 的 bias,然后把结果送进 activation function 里面,结束这回合的任务,留下结果 g(z),等待着与下一个 gate 输出的结果会合。 - input gate
首先用同一个 fed in data 乘以属于这个 gate 专属的 Weight,再加上属于这个 gate 的 bias,然后把结果送进 activation function 里面,得出结果 f(zi) 会识别出哪些新进的 data 可以通过于此,并与刚留下的结果 g(z) 相乘,把有 “通行证” 的 data 送往记忆门与旧的 data 相会。 - forget gate
首先用同一个 fed in data 乘以属于这个 gate 专属的 Weight,再加上属于这个 gate 的 bias,然后把结果送进 activation function 里面,的出结果 f(zf) 会识别出哪些旧的 data 可以被继续保留,而哪些该忘记,并与上回合留下来的记忆集 c 相乘,把有 “拘留权” 的 data 唤出并相加结合,结果就是:g(z) * f(zi) + c * f(zf) = c' 。 - memory cell
作为握有通行证与拘留权者的集合地出发,但是注意这边是没有专属的 Weight 要被相乘的,直接集合后送进 activation function 得出一个结果 h(c'),并且等待 “放行证” 的领取。该回合存活于此的 data 则会继续在下回合作为旧的 data 通过 forget gate 执行新一轮的筛选。 - output gate
首先用同一个 fed in data 乘以属于这个 gate 专属的 Weight,再加上属于这个 gate 的 bias,然后把结果送进 activation function 里面,得出的结果 f(zo) 就是根据前面运算最后的出来放行证的 “张数” ,最后用相乘的方法: h(c') * f(zo) 把证发给指定的数据顺利输出,并作为下一次要输入的一部分。
在实际写代码的时候,四个 gates 对应到的不同 Weights 会作为不同的 vector 互補干涉的獨立存在,並且 vector 裏面包含不同 dimension 的元素就是根據每層同一個 input 位置的多寡而定,每次每層的 unit cell 輸入的運算元素都只是這些總的 vector 其中一個 dimension 的東西。所以 RNN 跟别的神经网络最大的差别就是其 input data 要被放入 4 个地方做不同的处理,并把个别处理出来的元素再彼此相加相乘和 activation function 搅在一起,而不像之前不含时序问题的 NN 一般,一个 input data 对应到一个地方处理完后就可以了,也因为如此,LSTM 的参数量是一般 NN (包含一般 RNN) 所需的 4倍。
Peephole
实际应用中,除了本身新的 data 和历史 data 作为 input 端考虑外,还会把存在 memory cell 里面的元素纳入考虑范围中,把这三个参考元素并在一起再去乘以四个藏在不同 vectors 里面的 z 值。把 c‘ 也参考进来的这个动作就是 peephole 的精髓了(如上图 ct 的遭遇)。
当然上面这些内容都是最底层的原理,实际在写代码的时候,有个 python module called: keras 里面直接涵盖了上述内容的功能,只要一个呼叫就可以完事了,是个非常值得探索的工具!里面还包含了 LSTM & GRU & SimpleRNN 三种模式,其中要属 LSTM 最难,其他都是 LSTM 的简化版本。但是第二招说明了那么久,增加了那么多繁琐的细节,实际为了达到的功能还是要解决 Gradient Descent 在 SimpleRNN 没办法良好收敛的问题。
Backpropagation Through Time
但凡是神经网络,就离不开梯度下降与反向传播这两名大将的陪同,RNN 也不例外,不过相对于前面的 Neural Network 操作状态,RNN 的训练途径并不是一路顺岁的下降过程,原因是其 function 画成可视化的结果所呈现出来的崎岖表面与陡峭地形,在训练前就已经作为一个 Hyperparameter 被定死的 learning rate 要是遇到了踩在陡峭悬崖上的超大梯度,结果就是步距超大飞出了掌控范围从此永远别想收敛。
因此,Gradient Clipping 如上面的三行代码就是用来限制此一情况让事情不发生,当 update 的值超过一定的大小时,就让值等于我们能接受的设定范围,并继续下一循环。但是即便如此,Gradient Exploding or Vanishing 的问题还是存在于 SimpleRNN model 当中,随着神经网络的层数加多,time sequence 里面同样的 Weight 值会不断的重复使用,造成问题越来越严重,所以同样需要 LSTM 来拯救。
Memory Cell
相较于一般的 model,LSTM 多了一个 memory cell 的构造,并且与其直接按照原来的计算路径反推出 Backpropagation 的结果,取而代之的是让 Backpropagation 去计算 memory cell 的梯度,不但绕开了 tanh 的繁重资源占据问题,且梯度计算的值只是 matrix 里面其中一个(或是几个)元素(影片里面称作:elementwise multiplication),而不是 full matrix multiplication 这种比较不好的出结果的情况。LSTM 里面的 cell state 就如同提供了 GD 在计算的时候一个高速公路,可以快狠准的朝向目标前进。
可以这么做的原因就在于,每一个 LSTM 的 output 都是 “该回合的 input + 当时还记得在 Cell 里面的 data”,所以可以直接从 Cell 着手去影响整个 network output 的输出。
But here is an exceptional case written in one published paper: Vanilla RNN initialized with Identity matrix + ReLU activation function. The main point is that SimpleRNN model can easily beat back LSTM model by initializing with Identity matrix and using ReLU activation function.
直到现在,很多 RNN 的 model 都还是基于 LSTM 的原理去改进,会有些微的优化,但是整体而言并没有大幅的效能提升。
下节链接: