【机器学习】线性回归算法分析
AI
人工智能时代,机器学习,深度学习作为其核心,本文主要介绍机器学习的基础算法,以详细线介绍线性回归算法及其数学原理探究,做到知其然知其所以然,打好理论基础。
目录
机器学习及人工智能
机器学习分类
有监督学习
无监督学习
线性回归算法
线性回归
代价函数
数学模型
最小二乘法
算法介绍
数学原理
高斯分布
算法局限性
梯度下降算法
方向导数
梯度
数学原理
单元算法实现
多元算法实现
矩阵迹算法
随机梯度下降算法
高斯-牛顿法
泰勒级数展开
Hesse矩阵
数学原理
算法局限性
总结
机器学习及人工智能

开门见山,上图简单而直观的表明了人工智能,机器学习,深度学习的关系及区别,人工智能范畴最广,机器学习,深度学习逐步缩小;其实机器学习与深度学习可以看作人工智能的内部模型提炼过程,人工智能则是对外部的智能反应。
人工智能
人工智能(Artificial Intelligence),学术定义为用于研究,模拟及扩展人的智能应用科学;AI在计算机领域研究涉及机器人,语言识别,图像识别,自然语言处理等。AI的研究会横跨多门学科,如计算机,数学,生物,语言,声音,视觉甚至心理学和哲学。
其中AI的核心是做到感知,推断,行动及根据经验值进行调整,即类似人类的智慧体智能学习提升。
深度学习

深度学习则泛指深度神经网络学习,如卷积神经网络(Convolutional Neural Nets,CNN),把普通神经网络从3-4层升华到8-10层从而获取更精准模型,其应用如图像视频识别等。
人工智能,神经网络并非什么新鲜事物,早在20-30年前就已经诞生,而深度学习则借助因互联网而诞生的大数据,及近些年发展的强大运算能力(图形处理GPU)而大放光彩,甚至推动引爆了新一代的人工智能。
机器学习
机器学习的学究的定义为“计算机程序如何随着经验积累自动提高性能”,经典英文定义为
“A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.”,即“对于某类任务T和性能度量P,如果一个计算机程序在T上以P衡量的性能随着经验E而自我完善,那么我们称这个计算机程序在从经验E学习”, 通俗点说既是让机器来模拟人类来学习新的知识与技能,重点是不是通过某精妙算法而达成,而是让程序去通过学习发现提高,举一反三, 正所谓授之以鱼不如授之以渔。
2
机器学习分类
机器学习在学习的方法广义上分为有监督学习与无监督学习。

有监督学习(Supervised Learning)
监督学习,通常对具有标记分类的训练样本特征进行学习,标记即已经知道其对应正确分类答案;而学习则本质是找到特征与标签(正确答案)之间的关系(函数),从而当训练结束,输入无标签的数据时,可以利用已经找出的关系方法进行分析得出数据标签。
监督学习类似我们在学校的学习,通常的题目都会有“正确答案”,以便于我们每学期学习结束(训练),参加未知的考试作为检验。
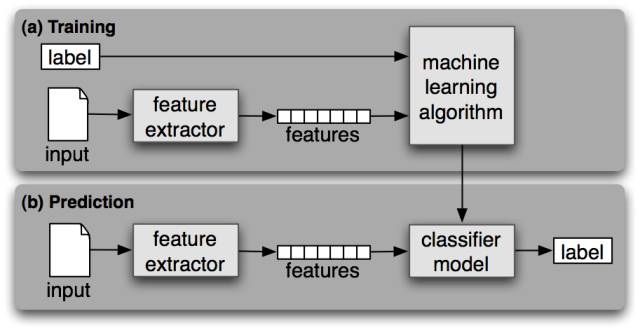
上图为监督学习的模型及流程:
获取数据并确定所处理数据类型
确定并提取训练数据集的特征(feature)
选择机器学习方法如向量机或决策树
获取最终机器模型
对机器学习模型进行评估
监督学习方法及用途
常用的监督机器学习方法有如人工神经网络,决策树,传统贝叶斯分类器,支撑向量机(SVM)等。
监督学习的主要用途通常用来进行样本分类与回归(找到最为接近的函数用于预测),而又根据其输出结果连续还是离散分为回归分析(Regression)与分类(Classification)。
无监督学习(Unsupervised Learning)
反之,无监督学习则通常学习数据只有特征向量,没有标签(答案),学习模型通过学习特征向量发现其内部规律与性质,从而把数据分组聚类(Clustering)。
无监督学习更类似我们的真实世界,去探索发现一些规律及分类。
举个例子,如果把监督学习看作未成年时在家长及老师的“监督”下做告知正确的事,则无监督学习就是成年后踏入社会,自己去探索,发现,适应社会了。
无监督学习方法及用途
常用的无监督学习方法有: K-Means, 层次化聚类(Hierarchical Clustering),社交网络分析,一些数据挖掘算法等。
无监督学习的用途则主要用来在未知(无标签)数据中发现相似或者隐藏结构并进行聚类(Clustering),或者发现数据对应输入空间的分布之密度估计等。
当然对于数据样本介于无标记及部分标记之间,这种机器学习则被称为半监督学习(semi-supervised learning),我们暂不介绍。
3
线性回归算法
上文提到了一些常用的机器学习算法,我们来看一下学习算法的概览分类图:

总体来说,机器学习中的回归算法的本质是通过对样本数据的收集,给出假设的函数模型,而此函数包含未知参数,机器学习的过程就是解方程或者找到最优解,当验证通过后,从而可以用该函数去预测测试新数据。
线性回归
回归,统计学术语,表示变量之间的某种数量依存关系,并由此引出回归方程,回归系数。
线性回归(Linear Regression),数理统计中回归分析,用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,其表达形式为y = w'x+e,e为误差服从均值为0的正态分布,其中只有一个自变量的情况称为简单回归,多个自变量的情况叫多元回归。
?注意,统计学中的回归并如线性回归非与严格直线函数完全能拟合,所以我们统计中称之为回归用以与其直线函数区别。
举个Andrew Ng机器学习讲义中美国俄亥俄州Portland Oregon城市房屋价格为例:
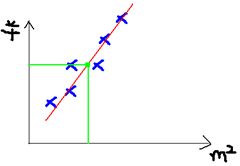
这个例子中近简化使用房屋面积一个因子作为自变量,y轴对应其因变量房屋价格。所以我们机器学习的线性回归就变为对于给定有限的数据集,进行一元线性回归,即找到一个一次函数y=y(x) + e,使得y满足
当x={2104, 1600, 2400, 1416, 3000, ... }, y={400, 330, 369, 232, 540, ... } 如下图所示:
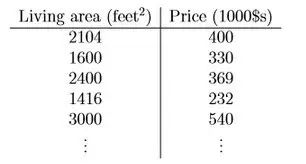
对于线性方程的求解,是属于线性代数的范畴。
首先要判断是否有解及是否有唯一解;其次具体求解方法则有矩阵消元法,克莱姆法则,逆矩阵及增广矩阵法等等。
对于大多数给定数据集,线性方程有唯一解的概率比较小,多数都是解不存在的超定方程组。
对于这种问题,在计算数学中通常将参数求解问题退化为求最小误差问题,找到一个最接近的解,即术语松弛求解。
回到上述Ng的房价问题,我们先简化给出假设函数(Hypothesis Function)即我们目标的近似函数或者需要拟合的直线记为:
其中
为我们需要求的参数,而参数的改变将会导致假设函数的变化,如:

在求解上述参数之前,我们有必要找到一种方法来衡量我们找到的函数是否为最优解,即代价函数。
代价函数(Cost Function)
对于回归问题,常用的用于衡量最优解的代价函数为平方误差。
平方误差的思想就是将实际样本数据值与我们拟合出的线做对应差值,即计算差距。
而为了减少由于极端数据的影响而造成的巨大波动,通常采用类似方差来减少个别数据影响,至于选择平方和作为估计函数,则需从概率分布角度了解其公式来源(统计学中,残差平方和函数可以看成n倍的均方误差),除以m则计算平均值,系数1/2则是纯数学简化(最小值的1/2仍然是最小值,不改变整体性质),其目的是当求导后相乘则消去系数,由此导出以下代价函数:
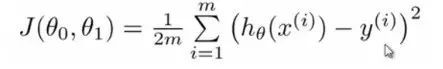
有了代价函数,从数学上来看,我们求解最优解的问题继而转而变成如何求函数的最小值:
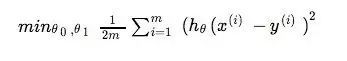
即cost函数J是基于theta的函数,用来检测我们的theta参数从而得到我们的假设函数。
最小值
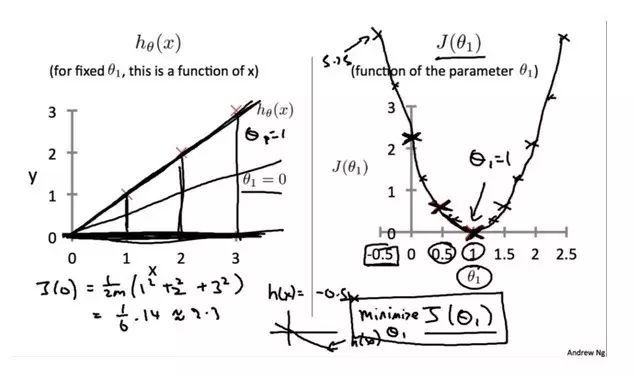
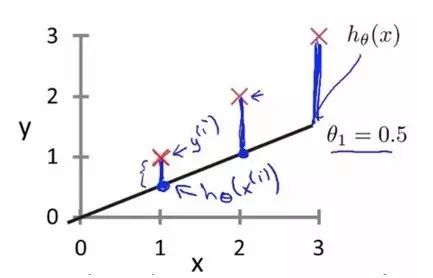
简化令之只有theta-1
上图是当对假设函数进行简化,使得theta-0 = 0,即只有一个参数theta-1,并假设给定样本数据为y ={(1,1), (2,2),(3,3)}; 当我们不断尝试给定theta-1,如0,0.5, 1时也得到J={(0, 2.3),(0.5, 0.58),(1,0)} 等等数据,其连线图形为右边的图形,可以看到对于当前案例,图形其J代价当theta = 1时有极小值。
其实大家可以看出,从数学角度,上述简化后的代价函数为一元二次方程,其在theta=1可导,并且导数为0,并且在theta=1处二阶可导,二阶导数大于0,所以在theta=1处取得极小值。
其数学原理见如下定理:

theta-0,theta-1
我们可以采用上述一个theta-1的方法对其代价函数求导得出其极值。

将 J(θ1,θ0) 分别对 θ1 和 θ0 求导,得

我们令上式等于零,从而可以得到θ1 和 θ0 的闭式closed-form(解析解,显性表达式;显式解)解:
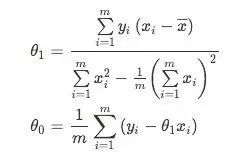
其中,
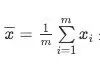
是x的均值。
实际上,对于两个参数θ1,θ0的代价函数,其图形J(θ1,θ0) 为一个曲面:

而我们上述求导过程,即试图找到曲面的最低点。
4
最小二乘法
最小二乘法
上述代价函数中使用的均方误差,其实对应了我们常用的欧几里得的距离(欧式距离,Euclidean Distance), 基于均方误差最小化进行模型求解的方法称为“最小二乘法”(least square method),即通过最小化误差的平方和寻找数据的最佳函数匹配;
当函数子变量为一维时,最小二乘法就蜕变成寻找一条直线;
推广到n个变量(n维),Hypothesis Function为:

其对应均方误差表示为如下矩阵:
之中:

对 θ 求导得:
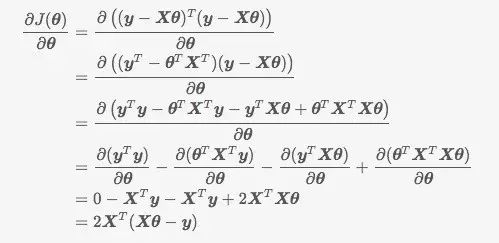
即结果为:

根据微积分定理,令上式等于零,可以得到 θ 最优的闭式解。当
为满秩矩阵或正定矩阵时,可解得
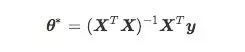
上式对于矩阵的求导,我们可以用以下图表简单展示:

数学原理
微积分角度来讲,最小二乘法是采用非迭代法,针对代价函数求导数而得出全局极值,进而对所给定参数进行估算。
计算数学角度来讲,最小二乘法的本质上是一个线性优化问题,试图找到一个最优解。
线性代数角度来讲,最小二乘法是求解线性方程组,当方程个数大于未知量个数,其方程本身 无解,而最小二乘法则试图找到最优残差。
几何角度来讲,最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影。
概率论角度来讲,如果数据的观测误差是/或者满足高斯分布,则最小二乘解就是使得观测数据出现概率最大的解,即最大似然估计-Maximum Likelihood Estimate,MLE(利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值)。
对于误差不符合高斯分布的,广义误差分布(广义误差用来描述一类中间高两边低连续且对称的概率密度函数):
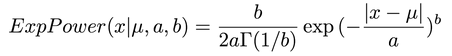
其中,当b=2时,退化为高斯分布;而当b=1时,则退化为拉普拉斯分布(最小一乘法),如一些长尾(long tail)的数据,经常服从拉普拉斯分布,对他们来说最小一乘才是更好的解法。。
高斯分布
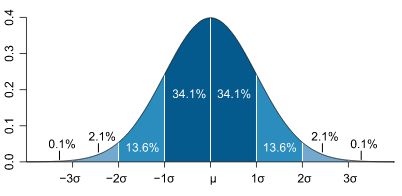
局限性
最小二乘法算法简单,容易理解,而然在现实机器学习却有其局限性:
并非所有函数都可以求出驻点,即导数为0的点,f(x)=0
求解方程困难,或求根公式复杂(引入泰勒公式展开?)
导数并无解析解,(多数函数无解析解)
最小二乘法的矩阵公式,计算一个矩阵的逆是相当耗费时间的, 而且求逆也会存在数值不稳定的情况 (比如对希尔伯特矩阵求逆就几乎是不可能的)
5
梯度下降算法
梯度下降算法(Gradient Descent)
正是由于在实际中,最小二乘法遇到的困难和局限性,尤其是多数超定方程组不存在解,我们由求导转向迭代逼近。
先看一下标准梯度的数学定义:
方向导数
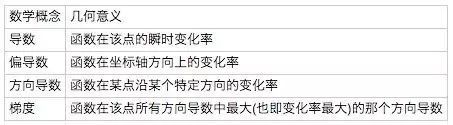
普通的偏导数是多元函数沿坐标轴的变化率,方向导数则考虑多元函数沿任意方向的变化率。
如下图考虑一个三维空间的方向导数:

简单来说,方向导数即研究在某一点的任意方向的变化率,是偏导数的广义扩展。
梯度
梯度则基于方向导数,是一个向量而非数,梯度代表了各个导数中,变化趋势最大的那个方向。
来看一下数学的严谨定义:
定义 设函数z=f(x, y) 在平面区域D内具有一阶连续偏导数,则对于每一点(x, y) 属于 D,都可定出一个向量
这向量称为函数z= f(x, y) 在点P(x, y) 的梯度,记作 grad f(x, y),即
根据数学知识,我们知道上述沿梯度方向的方向导数达最大值,即梯度的方向是函数f(x, y)或者我们关注的目标函数在这点P(x, y)增长最快,或者函数值变化最快的方向,负梯度方向是减小最快的方向,如下图。
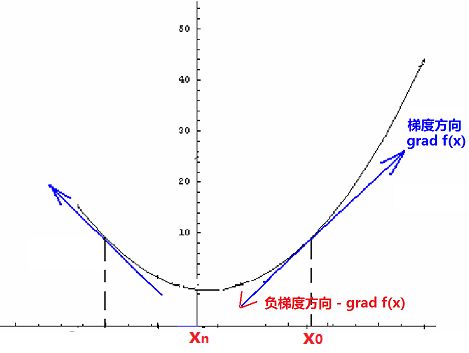
在机器学习中,上述的f(x, y)即是我们代价函数,如上图,当我们目标求f(x, y)的极小值时,我们可以先任意选取一个初始点,如x0, 让其沿着梯度负方向,依次走到x1,x2,x3,... xn,迭代n次,这样可以最快到达极小值点xn。
举个Ng中三维的例子,比如我们站在山上某一地点,梯度所指示的方向是高度变化最快的方向,你沿着这个方向走,可以最快的改变你所在位置的高度(增加或者减少),即如果你一直沿着梯度走,你可以最快到达某个顶峰或者谷底。

可以看出,初始点的选择不同,所计算出的极小值也不尽相同。
数学原理
我们来看一下标准梯度下降定义:
梯度下降算法也是一种优化算法,是求解无约束多元函数极值最早的数值方法,通常也被称作最速下降法。其目的是找到一个局部极小值点;其目标与最小二乘法相同,都是使得估算值与实际值的总平方差尽量小。
而其实现上,则采用计算数学,迭代法,先给定一初始点,然后向下降最快的方向调整,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,梯度下降算法不可避免的会存在陷入局部极小值的情形,这也是梯度下降算法的重大缺陷,其改进大多是在这两方面下功夫。
单元线性回归梯度算法实现
给定一个初始的θ0,θ1(仅以2参数为例)
不断改变θ0,θ1从而减少J(θ0,θ1)的值,具体做法是求导。直到最终收敛。
我们仍旧针对线性回归模型,包含θ0,θ1两个参数为例:

把假设函数h带入代价函数J(θ0,θ1)中,并分别求偏导数:

至此,得到计算机容易迭代的算法,整个过程序算法概括如下:

批次梯度下降(Batch Gradient Descent)
可以看到上述每次迭代都需要计算所有样本的残差并加和,所以又称作批次梯度下降(Batch Gradient Descent)。
学习率
上图中的系数a,通常称作学习率,用来控制下降的幅度。如果学习率太小,θ的值每次变化很小,梯度下降会很慢;
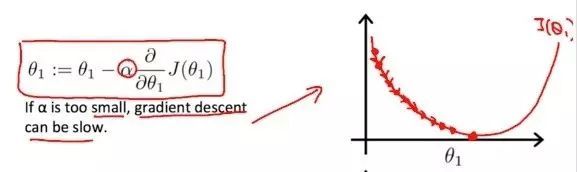
反之,如果学习率过大,θ的值每次变化也会很大,直接越过极小值,甚至无法收敛到达最低点。

多元线性回归梯度算法实现
上述都是简单的单元线性回归-梯度下降,我们再继续扩展至多元回归的梯度下降。
对于多元来讲(即由多个维度的样本数据,比如房价数据除了房屋面积大小,还有房间数,楼层,房龄,朝向,地理位置等,增加到多维)。
其对应的假设函数为如下:
或者用代数的简化记法:
θ,x都是向量。
其对应的多元代价函数:

所以对应的多元梯度算法如下:

对J(θ)求导:

多元矩阵迹求解法
对于多元函数的梯度下降通常引入矩阵算法来加速。
对于一个多元函数,用代数矩阵来表示,其对应的导数表示为如下:

定义矩阵的迹(Trace)
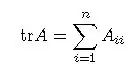
根据矩阵定理, 推导出如下:
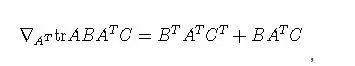
对J(θ)求导:

令上式为0,即得到目标θ向量:

上述充分展现了数学的神奇,矩阵法的优点是不需要多次迭代,一次计算机可以得出精确结果,然而当数据量大,对于矩阵乘法,逆的计算复杂度也大大增加,所以更适用于小规模数据。
6
随机梯度下降算法
我们在上文看到梯度下降算法中的学习率对收敛速度甚至能否收敛有至关重要的影响,另外在样本数据集便成大规模海量时,简单的梯度/批次下降算法并不太适合,在此引入随机梯度下降算法。
随机梯度下降算法的理念,其实是借鉴了随机样本抽样的方式,并提供了一种动态步长的策略,希望做到又优化精度,同时又满足必要的收敛速度。
随机梯度下降算法(Stochastic Gradient Descent)
每次迭代并非计算训练集中所有数据,而仅随机抽取了训练集中部分样本数据进行梯度计算,从而可以有效避免陷入局部极小值情况(上文有提到)。
然而天下无免费的午餐,鱼和熊掌无法兼得,同样随机梯度下降算法在平衡精度与迭代次数,牺牲了一部分精度,增加了一定数量的迭代次数(增加的迭代次数远远小于样本总量),换取了整体的优化效率提升。
7
高斯-牛顿算法
高斯-牛顿法
高斯-牛顿法是另一种经常用来求解非线性最小二乘的迭代法,其原理是利用了泰勒展开公式,其最大优点是收敛速度快。
Taylor 级数求得原目标函数的二阶近似:

把 x 看做自变量, 所有带有 x^k 的项看做常量,令一阶导数为 0 ,即可求近似函数的最小值:

Hesse矩阵
上边的Hesse矩阵,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。
算法原理
本质上来看,牛顿法是二阶收敛,而梯度下降则为一阶收敛,所以牛顿法更快。简单来说,梯度下降是从所处位置选择一个坡度最大的方向走一步,而牛顿法则在选择方向时,不仅考虑坡度,还会考虑下一步的坡度是否会变得更大。
几何意义:
几何上来说,牛顿法是用一个二次曲面去拟合当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,如下图:

通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
对于二元的情况,根据上述泰勒展开公式及求导,取0,可以得到如下迭代公式:

这样,我们就可以利用该迭代式依次产生的序列{x1,x2,x3,... xk}才逐渐逼近f(x)的极小值点了。
牛顿算法局限性
每种算法都有其适用性,牛顿算法主要局限性如下:
可以看出,因为我们需要求矩阵逆,当Hesse矩阵不可逆势无法计算
矩阵的逆计算复杂度为n的立方,当规模很大时,计算量超大,通常改良做法是采用拟牛顿法如BFGS,L-BFGS等
如果初始值离局部极小值太远,Taylor展开并不能对原函数进行良好的近似
8
总结
机器学习,算法涉及大量高等数学,线性代数,概率统计,计算数学等推论,论证,难度非常大。
本文内容借鉴了很多资料,尤其是斯坦福大学Ng的教材,感谢!
写作耗时耗力,希望有机会能继续机器学习更多的算法学习介绍。
本文由技术极客授权转载


