MIT算法导论第一课——插入排序与归并排序c++实现

最近开始重新温习C++以及学习麻省理工的算法导论课，然后以后会逐渐更新点所学到的东西。

第一天学习的主要是各种符号及概念。

然后主要讲了排序问题的时间复杂度，先来看看这两种算法的实现

插入排序法：

其算法原理就是按照顺序从数组中选择数字，与其之前的数字进行比较，直到遇到比自己小的数字就停下来，插在这个比自己小的数字之后，以此类推。实现函数如下：

template
int length(T& arr){
	return sizeof(arr)/sizeof(arr[0]);
}//用于计算数组长度

template
void insertion_sort(T a[]，int n){//n为数组长度，注意不可以在该函数里对数组a进行计算长度
	for(int j = 1;j=0 && a[i]>=key){//前面的数字已经排列好，那么就可以理解为比自己大的都按原顺序后移
			a[i+1] = a[i];
			i--;
		}
		a[i+1] = key;//直到遇到比自己小的，就不再动了
	}
}

归并排序法：主要思想是分治法思想，先分组后合并，但是分组的思想就交给一次又一次的迭代了，而我们只需要考虑合并的事儿就好。代码如下：

//归并
void Merge(int *a,int begin1,int begin2,int end1,int end2,int *tmp){
	int index = begin1;
	int i = begin1;
	int j = begin2;
	while(i<=end1&&j<=end2){//将两个分开的数组归并在一起
			if(a[i]<=a[j])
				tmp[index++] = a[i++];
			else 
				tmp[index++] = a[j++];
	}
	//最后谁剩了，就按照原来的顺序放到后面排着
	while(i<=end1) tmp[index++] = a[i++];
	while(j<=end2) tmp[index++] = a[j++];
	//将排好的数组段放回原数组中
	memcpy(a+begin1,tmp+begin1,sizeof(int)*(end2-begin1+1));
}
//排序
void Merge_sort(int *a,int begin,int end,int *tmp){//归并排序
	if(begin >= end) return;
	int mid = (begin + end)/2;
	Merge_sort(a,begin,mid,tmp);
	Merge_sort(a,mid+1,end,tmp);
	Merge(a,begin,mid+1,mid,end,tmp);
}

接下来分析下时间复杂度的问题：

对于插入排序法来说，其基本操作在于数组元素的大小比较，也就是在两个循环内的数值的比较，那么在最差情况（Worst-Case）下，插入排序法时间复杂度。

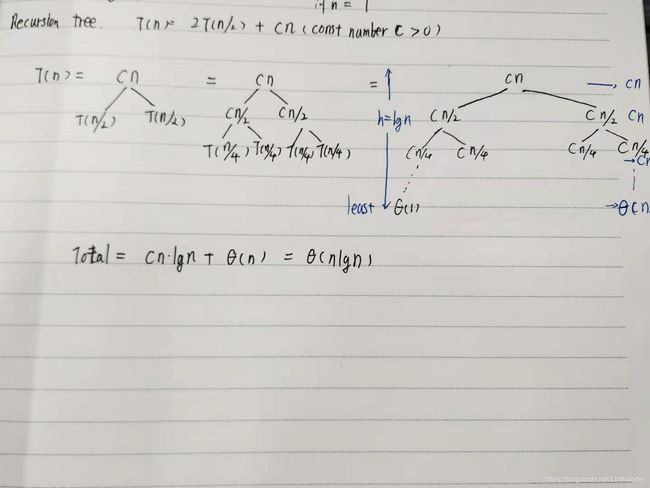
对于归并排序法来说，其可以利用树状图来表示其时间复杂度，如图（手绘，有点丑）：

那么在最差情况（Worst-Case）下，归并排序法时间复杂度。

 

最后附上完整两端代码：

插入排序：

#include
#include
using namespace std;
template
int length(T& arr){
	return sizeof(arr)/sizeof(arr[0]);
}
template
void insertion_sort(T a[],int n){
	for(int j = 1;j=0 && a[i]>=key){
			a[i+1] = a[i];
			i--;
		}
		a[i+1] = key;
	}

}
template
void Print(T a[],int n){
	for (int i=0;i

归并排序：

#include
#include
using namespace std;

//归并
void Merge(int *a,int begin1,int begin2,int end1,int end2,int *tmp){
	int index = begin1;
	int i = begin1;
	int j = begin2;
	while(i<=end1&&j<=end2){//将两个分开的数组归并在一起
			if(a[i]<=a[j])
				tmp[index++] = a[i++];
			else 
				tmp[index++] = a[j++];
	}
	//最后谁剩了，就按照原来的顺序放到后面排着
	while(i<=end1) tmp[index++] = a[i++];
	while(j<=end2) tmp[index++] = a[j++];
	//将排好的数组段放回原数组中
	memcpy(a+begin1,tmp+begin1,sizeof(int)*(end2-begin1+1));
}
//排序
void Merge_sort(int *a,int begin,int end,int *tmp){//归并排序
	if(begin >= end) return;
	int mid = (begin + end)/2;
	Merge_sort(a,begin,mid,tmp);
	Merge_sort(a,mid+1,end,tmp);
	Merge(a,begin,mid+1,mid,end,tmp);
}
template
int length(T& arr){
	return sizeof(arr)/sizeof(arr[0]);
}

void Print(int a[],int n){
	for (int i=0;i

后面会接着学习然后写一些自己的理解以及发布代码之类的