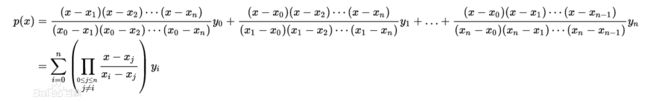E. Guess the Root （拉格朗日多项式+交互）

题目链接：哆啦A梦传送门

题意：现在有一个未知系数的多项式

题目要你找出一个 x1，使得f(x1)%(1e6+3)==0。

但不知道系数ai的值，你可以询问黑匣子，询问一个值x2，然后它会返回f(x2)%(1e6+3)的值，你最多有50次询问。

 

题解：看到这个多项式，自然很容易知道，只需询问11次就能知道所有的系数（我们这里不求系数）。

现在有一个叫拉格朗日多项式，它可以很完美的求出，每次想询问的值x2，f(x2)的结果。

此图参考百度百科。

根据这个公式，我们只需询问10次，这时我们就有10对 (xi,yi)。暴力求解就行了。

第一篇是我写的纯暴力 O(mod*100)，显然复杂度有点大，但还是能在题目要求时限过。

 

#include

using namespace std;

#define INF 0x3f3f3f3f

typedef long long LL;


const LL mod=1e6+3;
LL fast(LL a,LL n)
{

    LL sum=1;

    while(n)
    {
        if(n&1) sum=sum*a%mod;
        n>>=1;
        a=a*a%mod;
    }
    return sum;
}

LL p[20];

/*
2 9 1 4 8 10 0 2 8 7 6
Output
1
Answer
1
*/

int main()
{
//    fflush(stdout);

    ///询问十次
    for(int i=0;i<=10;i++)
    {
         cout << "? " << i << endl;
    cin >> p[i];

        if(p[i]==0){ ///为0就直接输出了
            printf("! %d\n",i);
            return 0;
        }
        if(p[i]==-1){
            return 0;
        }
    }

    ///计算每一项的分母与yi
    for(LL i=0;i<=10;i++)
    {
        LL item=1;
        for(LL j=0;j<=10;j++){
            if(i==j) continue;
            item=(i-j+mod)%mod*item%mod;
        }

        p[i]=p[i]*fast(item,mod-2)%mod;
    }

    ///暴力枚举每个可能的值
    for(LL i=11;i<=mod;i++)
    {
        LL sum=0;
        ///枚举第j项
        for(int j=0;j<=10;j++)
        {
            LL item=1;
            for(LL k=0;k<=10;k++)
            {
                if((LL)j==k) continue;
                item=(i-k+mod)%mod*item%mod;
            }
            sum=sum+item*p[j]%mod;
            sum%=mod;
        }
        if(sum==0LL){
            cout<<"! "<

第二篇是拿已过人的。显然这篇复杂度为 O(mod*10*2)。

#include 

using namespace std;
typedef long long ll;

const ll mod = 1e6+3;

ll fastexp (ll a, ll b, ll n) {
  long long res = 1;
  while (b) {
      if (b & 1) res = res*a%n;
      a = a*a%n;
      b >>= 1;
  }
  return res;
}

int main() {
  vector p(11), re(mod);
  for (ll i = 1; i < mod; i++) {
    re[i] = fastexp(i, mod-2, mod);
  }


  for (int i = 0; i < 11; i++) {
    cout << "? " << i << endl;
    cin >> p[i];
    if (p[i] == -1) {return 0;}
    if (p[i] == 0) {
      cout << "! " << i << endl;
      return 0;
    }
  }

  for (int i = 0; i < 11; i++) {
    for (int j = 0; j < 11; j++){
      if (j == i) continue;
      p[i] = p[i]*re[(i-j+mod)%mod]%mod;
    }
  }
  for (int x = 11; x < mod; x++) {
    ll val = 0;

    ///直接就算项，每次分子补一个，那么分母就多一个，加个逆元就好了
    for (int i = 0; i < 11; i++) {
      val = (val +  p[i]*re[x-i])%mod;
    }

    ll item=1;
        for(int j=0;j<=10;j++){
            item=(x-j+mod)%mod*item%mod;
        }
        val=val*item%mod;
        val%=mod;
    if (val%mod == 0) {
      cout << "! " << x << endl;
      return 0;
    }
  }
  cout << "! -1" << endl;
  return 0;
}