noip2016天天爱跑步

我从来不惮以最坏的恶意来揣测自己的智商，然而我还不料它竟能低到如此地步！！！
终于明白为什么最近几次考试写一次lca挂一次，因为近来我lca的板子写错了

前（sai）言（hua）：

这道题看的时候想了好久，没有思路，决定写分治，按理说有80分，但是我写挂了只有40……
通过这次失败的分治经历我总结出来的教训是：有的数据点能在一起写就在一起写，写的太细反而浪费时间。
以及这道题我理解了好久才明白正解【所以一定要熟练掌握分治啊】

思路：

点i在路径上，如果点i的观察员刚好能观察到该路径上的玩家，需要满足的条件是：
1、假设S在i的子树中

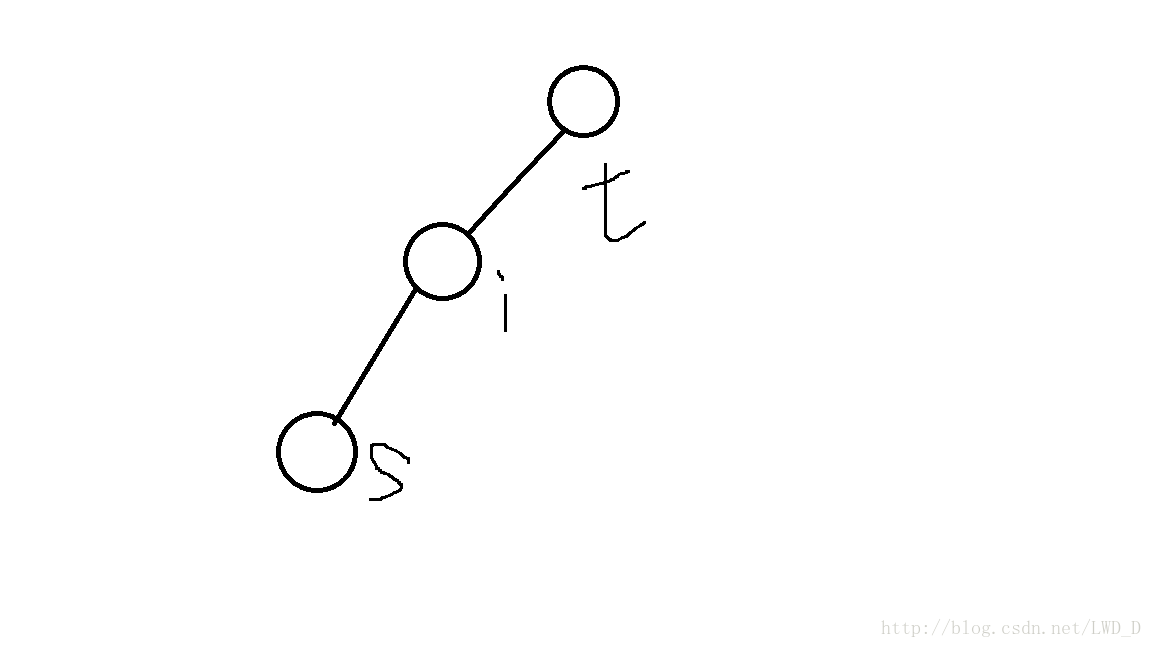
那么s和i的关系是：dep[i]+wat[i]=dep[s]
我们在遍历回溯到i点时，查询又在它的子树内又多少个s’满足条件
2、假设T在i的子树中

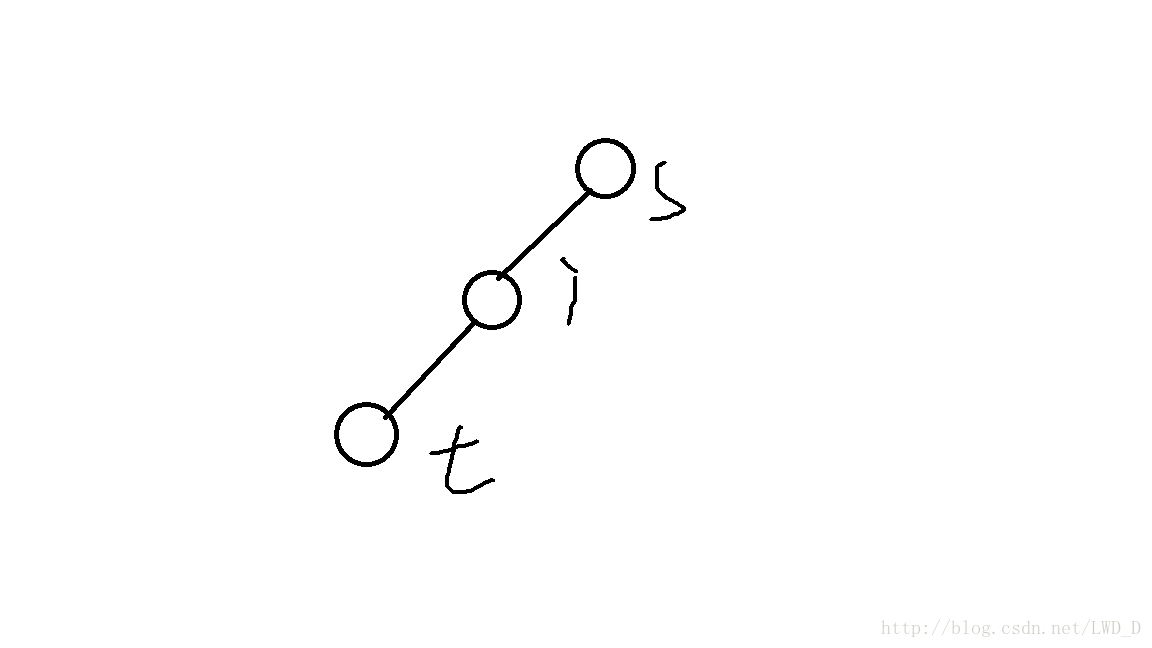
那么t和i的关系是：dep[i]-wat[i]=dep[t]-dis(s,t)
我们在遍历回溯到i点时，查询又在它的子树内又多少个t’满足条件

上述两种情况会导致一种情况被算重，那就是：

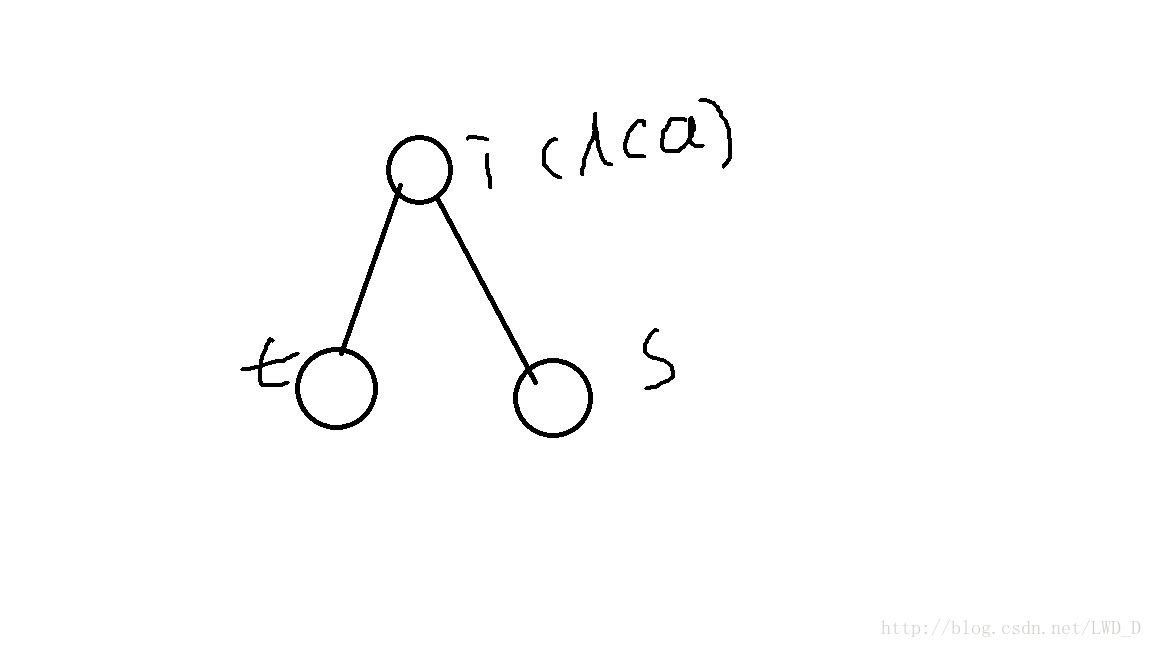
这时s和t都在i的子树内所以会被各算一次，我们可以需要去重：回溯到点u时，当u为lca且u为lca对应的s能被在u点的观察员观察到，那么就出现了这种情况，ans[u]–

也会导致算多一种情况：

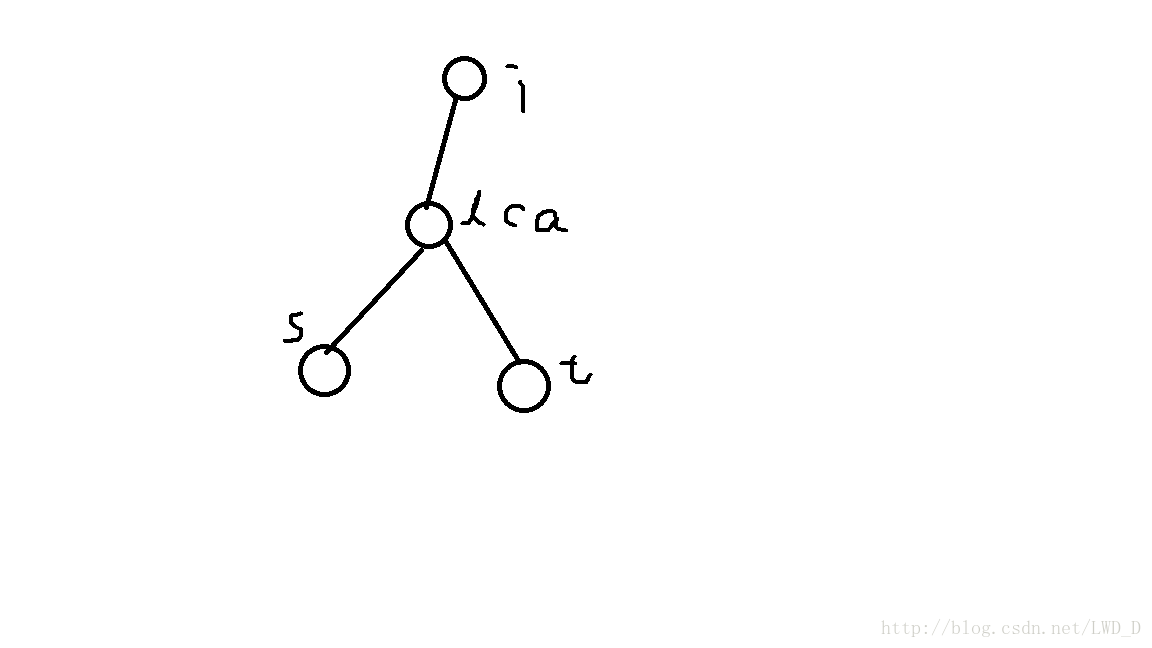
这时路径已经不经过i了，但按照之前所说的判断依据如果dep[i]+wat[i]=dep[s]/dep[i]-wat[i]=dep[t]-dis(s,t)，还是会被算作点i的观察员观察到了该路径的玩家。
为了避免算重这种情况，我们需要运用差分。
在ls[ lca] 处pushback｛dep[s]｝的值，在lt[ lca ]处pushback｛dep[t]-dis(s,t)｝。在dfs回溯到lca处，–down[dep[s]] （消除了点s对答案统计的影响）

最后就是实现时的一些细节了，比如down，up的使用，pre的使用，看代码还是很易于理解的。

#include
#include
#include
#include
using namespace std;
const int N=3e5,P=18,NUM=N;
int n,m;
int to[2*N],nxt[2*N],head[N],etot;
int wat[N];
int dep[N],anc[N][P+1];
int iss[N],down[N],up[4*N];
int ans[N];
vector<int> fot[N],ls[N],lt[N];
void adde(int u,int v)
{
    to[++etot]=v;
    nxt[etot]=head[u];
    head[u]=etot;
}
void dfs(int u,int fa)
{
    dep[u]=dep[fa]+1;
    anc[u][0]=fa;
    for(int p=1;p<=P;p++)
    anc[u][p]=anc[anc[u][p-1]][p-1];
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        dfs(v,u);
    }
}
int lca(int u,int v)
{
    if(dep[u]int t=dep[u]-dep[v];
    for(int p=0;t;t>>=1,p++)
    if(t&1) u=anc[u][p];
    if(u==v) return u;
    for(int p=P;p>=0;p--)//!!!
    if(anc[u][p]!=anc[v][p]) u=anc[u][p],v=anc[v][p];
    return anc[u][0];
}
void dfs2(int u,int fa)
{
    int pre=down[dep[u]+wat[u]]+up[dep[u]-wat[u]+NUM];  
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        dfs2(v,u);
    }
    down[dep[u]]+=iss[u];
    for(int i=0;ifor(int i=0;iif(ls[u][i]==dep[u]+wat[u]) ans[u]--;
        down[ls[u][i]]--;//利用差分思想在lca处-- 
    }
    for(int i=0;iint main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;iint u,v;
        scanf("%d%d",&u,&v);
        adde(u,v),adde(v,u);
    } 
    for(int i=1;i<=n;i++)
    scanf("%d",&wat[i]);
    dfs(1,1);
    for(int i=1;i<=m;i++){
        int s,t;
        scanf("%d%d",&s,&t);
        int l=lca(s,t);
        iss[s]++;
        int dis=dep[s]+dep[t]-2*dep[l];
        fot[t].push_back(dep[t]-dis+NUM);
        ls[l].push_back(dep[s]);//ls【i】 的意义：当i是lca时，它的s的dep【s】是多少 
        lt[l].push_back(dep[t]-dis+NUM);
    }
    dfs2(1,1);
    for(int i=1;i<=n;i++)
    printf("%d ",ans[i]);
    return 0;
}