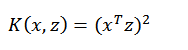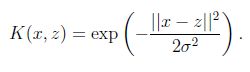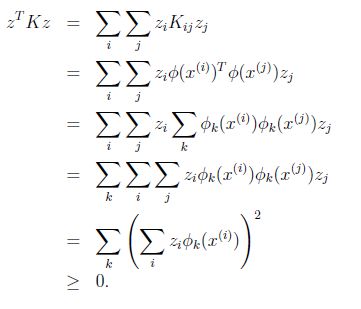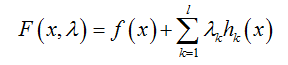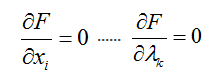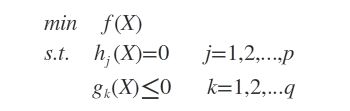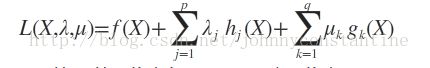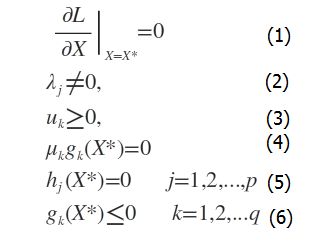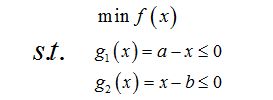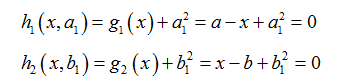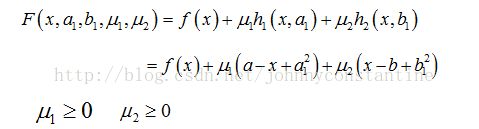支持向量机(三):核函数和KKT条件的理解
转:http://www.cnblogs.com/pursued-deer/p/7858122.html
1 核函数
1.1 核函数的定义
设χ是输入空间(欧氏空间或离散集合),Η为特征空间(希尔伯特空间),如果存在一个从χ到Η的映射
φ(x): χ→Η
使得对所有的x,z∈χ,函数Κ(x,z)=φ(x)∙φ(z), 则称Κ(x,z)为核函数,φ(x)为映射函数,φ(x)∙φ(z)为x,z映射到特征空间上的内积。
由于映射函数十分复杂难以计算,在实际中,通常都是使用核函数来求解内积,计算复杂度并没有增加,映射函数仅仅作为一种逻辑映射,表征着输入空间到特征空间的映射关系。至于为什么需要映射后的特征而不是最初的特征来参与计算,为了更好地拟合是其中一个原因,另外的一个重要原因是样例可能存在线性不可分的情况,而将特征映射到高维空间后,往往就可分了。
1.2 核函数的计算原理
将核函数形式化定义,如果原始特征内积是![]() ,映射后为
,映射后为![]() ,那么定义核函数(Kernel)为
,那么定义核函数(Kernel)为
到这里,我们可以得出结论,如果要实现该节开头的效果,只需先计算![]() ,然后计算
,然后计算![]() 即可,然而这种计算方式是非常低效的。比如最初的特征是n维的,我们将其映射到
即可,然而这种计算方式是非常低效的。比如最初的特征是n维的,我们将其映射到![]() 维,然后再计算,这样需要
维,然后再计算,这样需要![]() 的时间。那么我们能不能想办法减少计算时间呢?
的时间。那么我们能不能想办法减少计算时间呢?
先看一个例子,假设x和z都是n维的,
展开后,得:
这个时候发现我们可以只计算原始特征x和z内积的平方(时间复杂度是O(n)),就等价与计算映射后特征的内积。也就是说我们不需要花![]() 时间了。
时间了。
现在看一下映射函数(n=3时),根据上面的公式,得到
也就是说核函数![]() 只能在选择这样的
只能在选择这样的![]() 作为映射函数时才能够等价于映射后特征的内积。
作为映射函数时才能够等价于映射后特征的内积。
再看另外一个核函数,高斯核函数:
这时,如果x和z很相近(![]() ),那么核函数值为1,如果x和z相差很大(
),那么核函数值为1,如果x和z相差很大(![]() ),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
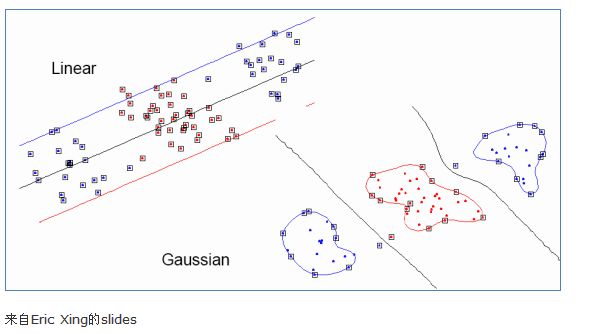
下面有张图说明在低维线性不可分时,映射到高维后就可分了,使用高斯核函数。
注意,使用核函数后,怎么分类新来的样本呢?线性的时候我们使用SVM学习出w和b,新来样本x的话,我们使用![]() 来判断,如果值大于等于1,那么是正类,小于等于是负类。在两者之间,认为无法确定。如果使用了核函数后,
来判断,如果值大于等于1,那么是正类,小于等于是负类。在两者之间,认为无法确定。如果使用了核函数后,![]() 就变成了
就变成了![]() ,是否先要找到
,是否先要找到![]() ,然后再预测?答案肯定不是了,找
,然后再预测?答案肯定不是了,找![]() 很麻烦,回想我们之前说过的。
很麻烦,回想我们之前说过的。
只需将![]() 替换成
替换成![]() ,然后值的判断同上。
,然后值的判断同上。
1.3 核函数有效性的判定
问题:给定一个函数K,我们能否使用K来替代计算![]() ,也就说,是否能够找出一个
,也就说,是否能够找出一个![]() ,使得对于所有的x和z,都有
,使得对于所有的x和z,都有![]() ?即比如给出了
?即比如给出了![]() ,是否能够认为K是一个有效的核函数。
,是否能够认为K是一个有效的核函数。
下面来解决这个问题,给定m个训练样本![]() ,每一个
,每一个![]() 对应一个特征向量。那么,我们可以将任意两个
对应一个特征向量。那么,我们可以将任意两个![]() 和
和![]() 带入K中,计算得到
带入K中,计算得到![]() 。i 可以从1到m,j 可以从1到m,这样可以计算出m*m的核函数矩阵(Kernel Matrix)。为了方便,我们将核函数矩阵和
。i 可以从1到m,j 可以从1到m,这样可以计算出m*m的核函数矩阵(Kernel Matrix)。为了方便,我们将核函数矩阵和![]() 都使用K来表示。如果假设K是有效地核函数,那么根据核函数定义:
都使用K来表示。如果假设K是有效地核函数,那么根据核函数定义:
可见,矩阵K应该是个对称阵。让我们得出一个更强的结论,首先使用符号![]() 来表示映射函数
来表示映射函数![]() 的第k维属性值。那么对于任意向量z,得:
的第k维属性值。那么对于任意向量z,得:
最后一步和前面计算![]() 时类似。从这个公式我们可以看出,如果K是个有效的核函数(即
时类似。从这个公式我们可以看出,如果K是个有效的核函数(即![]() 和
和![]() 等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(
等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(![]() )。这样我们得到一个核函数的必要条件:K是有效的核函数 ==> 核函数矩阵K是对称半正定的。
)。这样我们得到一个核函数的必要条件:K是有效的核函数 ==> 核函数矩阵K是对称半正定的。
Mercer定理表明为了证明K是有效的核函数,那么我们不用去寻找![]() ,而只需要在训练集上求出各个
,而只需要在训练集上求出各个![]() ,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
1.4 常见的核函数
1 线性核函数
线性内核是最简单的内核函数。 它由内积
表达式 :![]()
2 多项式核函数
多项式核是非固定内核。 多项式内核非常适合于所有训练数据都归一化的问题。
表达式:k(x,y)=(αx T y + c)d
可调参数是斜率α,常数项c和多项式度d。
3 高斯核函数
高斯核是径向基函数核的一个例子。
或者,它也可以使用来实现
![]()
可调参数sigma在内核的性能中起着主要作用,并且应该仔细地调整到手头的问题。 如果过高估计,指数将几乎呈线性,高维投影将开始失去其非线性功率。 另一方面,如果低估,该函数将缺乏正则化,并且决策边界将对训练数据中的噪声高度敏感。
4 指数的内核
指数核与高斯核密切相关,只有正态的平方被忽略。 它也是一个径向基函数内核。
5 拉普拉斯算子核
拉普拉斯核心完全等同于指数内核,除了对sigma参数的变化不那么敏感。 作为等价的,它也是一个径向基函数内核。
重要的是注意,关于高斯内核的σ参数的观察也适用于指数和拉普拉斯内核。
2 KKT 条件
KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法,不同之处在于应用的情形不同。有三种情况:无约束条件,等式约束条件,不等式约束条件。
2.1 无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
2.2 等式约束条件
设目标函数为f(x),约束条件为hk(x),l 表示有 l 个约束条件,如:
则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述,拉格朗日法这里在提一下,因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
定义拉格朗日函数F(x) :
其中λk是各个约束条件的待定系数。
然后解变量的偏导方程:
2.3 不等式约束条件
设目标函数f(x),不等式约束为g(x),添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中 f(x) 是原目标函数,hj(x) 是第j个等式约束条件,λj 是对应的约束系数,gk 是不等式约束,uk 是对应的约束系数。
此时若要求解上述优化问题,必须满足下述条件(也是我们的求解条件):
这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件,(2)是拉格朗日系数约束(同等式情况),(3)是不等式约束情况,(4)是互补松弛条件,(5)、(6)是原约束条件。
对于一般的任意问题而言,KKT条件是使一组解成为最优解的必要条件,当原问题是凸问题的时候,KKT条件也是充分条件。
2.4 举例说明
现有如下不等式约束优化问题:
此时引入松弛变量可以将不等式约束变成等式约束。设a1和b1为两个松弛变量,则上述的不等式约束可写为:
则该问题的拉格朗日函数为:
根据拉格朗日乘子法,求解方程组:
同样 μ2b1=0,来分析g2(x)起作用和不起作用约束。
于是推出条件:
搞了一天把支持向量机的前三篇写完了,肯定是写的不足,鉴于SVM难度大和本人的水平有限,只能做到这样了。不足的地方请各位博友多多指教,第四部分的支持向量机的应用,是根据机器学习实战一步步实现,会给出详细的代码介绍。