Opencv相机标定与3D重构---纹理对象的实时姿势估计

理论

在计算机视觉估计中，从n个3D到2D点对应的相机姿势是基本且易于理解的问题。 该问题的最一般版本需要估计姿势的六个自由度和五个校准参数：焦距，主点，纵横比和歪斜。 使用众所周知的直接线性变换（DLT）算法，可以建立至少6个对应关系。 但是，对问题进行了若干简化，这些简化成为提高DLT准确性的不同算法的广泛列表。

最常见的简化是假设已知的校准参数，即所谓的Perspective- * n * -Point问题：

问题公式：给定在世界参考系中表示的3D点pi与其在图像上的2D投影ui之间的一组对应关系，我们寻求检索相机的姿势（R和t）w.r.t. 世界和焦距f。

OpenCV提供了四种不同的方法来解决返回R和t的Perspective- * n * -Point问题。 使用以下公式可以将3D点投影到图像平面：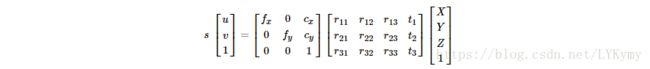

代码

您可以在OpenCV源库的samples / cpp / tutorial_code / calib3d / real_time_pose_estimation /文件夹中找到本教程的源代码。

本教程包含两个主要程序：

注册模型

• 该应用程序专用于没有要检测的对象的3D纹理模型。 您可以使用此程序创建自己的纹理3D模型。 此程序仅适用于平面对象，如果要对具有复杂形状的对象建模，则应使用复杂的软件来创建它。
• 应用程序需要要注册的对象的输入图像及其3D网格。 我们还必须提供用于拍摄输入图像的相机的固有参数。 需要使用绝对路径或应用程序工作目录中的相对路径指定所有文件。 如果未指定任何文件，程序将尝试打开提供的默认参数。
• 应用程序开始从输入图像中提取ORB特征和描述符，然后使用网格和Möller-Trumbore交集算法计算找到的特征的3D坐标。 最后，3D点和描述符存储在具有YAML格式的文件中的不同列表中，每个行是不同的点。 

模型检测

• 该应用的目的是在给定其3D纹理模型的情况下实时估计对象姿势。
• 应用程序开始以YAML文件格式加载3D纹理模型，其结构与模型注册程序中说明的结构相同。 从场景中，检测并提取ORB特征和描述符。 然后，使用cv :: FlannBasedMatcher和cv :: flann :: GenericIndex来进行场景描述符和模型描述符之间的匹配。 使用找到的匹配以及cv :: solvePnPRansac函数，计算摄像机的R和t。 最后，应用KalmanFilter以拒绝不良姿势。
• 如果您使用示例编译OpenCV，可以在opencv / build / bin / cpp-tutorial-pnp_detection`中找到它。 然后，您可以运行该应用程序并更改一些参数：

解释

• 读取3D纹理对象模型和对象网格。
• 为了加载纹理模型，我实现了类Model，它具有函数load（），它打开一个YAML文件，并使用相应的描述符获取存储的3D点。 您可以在samples / cpp / tutorial_code / calib3d / real_time_pose_estimation / Data / cookies_ORB.yml中找到3D纹理模型的示例。
• 在主程序中，模型加载如下：
• 为了读取模型网格，我实现了一个类Mesh，它具有一个函数load（），它打开一个* .ply文件并存储对象的3D点以及组合三角形。 您可以在samples / cpp / tutorial_code / calib3d / real_time_pose_estimation / Data / box.ply中找到模型网格的示例。
• 在主程序中，网格加载如下：
• 您还可以加载不同的模型和网格：
• 从相机或视频中获取输入。
• 要检测是必要的捕获视频。 通过传递它在机器中的绝对路径来完成加载录制的视频。 为了测试应用程序，您可以在samples / cpp / tutorial_code / calib3d / real_time_pose_estimation / Data / box.mp4中找到录制的视频。
• 然后算法是每帧计算帧：
• 您还可以加载不同的录制视频：
• 从场景中提取ORB特征和描述符。
• 下一步是检测场景特征并提取它的描述符。 为此，我实现了一个RobustMatcher类，它具有关键点检测和特征提取功能。 您可以在samples / cpp / tutorial_code / calib3d / real_time_pose_estimation / src / RobusMatcher.cpp中找到它。 在您的RobusMatch对象中，您可以使用OpenCV的任何2D特征检测器。 在这种情况下，我使用了cv :: ORB功能，因为它基于cv :: FAST来检测关键点，而cv :: xfeatures2d :: BriefDescriptorExtractor来提取描述符，这意味着它对于旋转来说是快速且健壮的。 您可以在文档中找到有关ORB的更多详细信息。
• 以下代码是如何实例化和设置功能检测器和描述符提取器：
• 使用Flann匹配器将场景描述符与模型描述符匹配。
• 这是我们检测算法的第一步。 主要思想是将场景描述符与我们的模型描述符进行匹配，以便将所找到的特征的3D坐标知道到当前场景中。
• 首先，我们必须设置我们想要使用的匹配器。 在这种情况下使用cv :: FlannBasedMatcher匹配器，它在计算成本方面比cv :: BFMatcher匹配器更快，因为我们增加了训练的特征收集。 然后，对于FlannBased匹配器，创建的索引是Multi-Probe LSH：由于ORB描述符而导致的高维相似性搜索的高效索引是二进制的。
• 您可以调整LSH和搜索参数以提高匹配效率：
• 其次，我们必须使用robustMatch（）或fastRobustMatch（）函数来调用匹配器。 使用这两个函数的不同之处在于其计算成本。 第一种方法在过滤良好匹配时速度较慢但更稳健，因为使用了两个比率测试和一个对称测试。 相比之下，第二种方法更快但不太稳健，因为只对比赛应用单一比率测试。以下代码是获取模型3D点及其描述符，然后在主程序中调用匹配器：
• 以下代码对应于属于RobustMatcher类的robustMatch（）函数。 此函数使用给定图像来检测关键点并提取描述符，使用给定模型描述符的两个最近邻提取描述符进行匹配，反之亦然。 然后，将比率测试应用于两个方向匹配，以便去除这些匹配，其中第一和第二最佳匹配之间的距离比大于给定阈值。 最后，应用对称性测试以便去除非对称匹配。
• 在匹配过滤之后，我们必须使用获得的DMatches向量从找到的场景关键点和我们的3D模型中减去2D和3D对应关系。 有关cv :: DMatch的更多信息，请查看文档。
• 您还可以更改比率测试阈值，要检测的关键点数量以及是否使用强健匹配器：
• 使用PnP + Ransac进行姿势估计。
• 一旦使用2D和3D对应，我们必须应用PnP算法来估计相机姿势。 我们必须使用cv :: solvePnPRansac而不是cv :: solvePnP的原因是，在匹配之后，并非所有找到的对应关系都是正确的，并且如同不同，存在错误的对应关系或者也称为异常值。 随机样本共识或Ransac是一种非确定性迭代方法，其根据观察到的数据估计数学模型的参数，随着迭代次数的增加产生近似结果。 在对Ransac进行应用之后，将消除所有异常值，然后以一定的概率估计相机姿态以获得良好的解决方案。
• 对于相机姿势估计，我实现了一个类PnPProblem。 该类有4个属性：给定的校准矩阵，旋转矩阵，平移矩阵和旋转平移矩阵。 您用于估计姿势的相机的固有校准参数是必要的。 为了获得参数，您可以使用方形棋盘和使用OpenCV教程的相机校准来检查相机校准。
• 以下代码是如何在主程序中声明PnPProblem类：
• 以下代码是PnP Problem类如何初始化其属性：
• OpenCV提供四种PnP方法：ITERATIVE，EPNP，P3P和DLS。 根据应用类型，估算方法将有所不同。 在我们想要进行实时应用的情况下，更合适的方法是EPNP和P3P，因为它在寻找最优解时比ITERATIVE和DLS更快。 然而，EPNP和P3P在平面表面前不是特别坚固，并且有时姿势估计似乎具有镜面效果。 因此，在本教程中使用的是ITERATIVE方法，因为要检测的对象具有平面。
• OpenCV Ransac实现要求您提供三个参数：停止算法之前的最大迭代次数，观察点和计算点之间的最大允许距离，将其视为内部，以及获得良好结果的置信度。 您可以调整这些参数以提高算法性能。 增加迭代次数可以获得更准确的解决方案，但需要更多时间才能找到解决方案。 增加重投影错误会缩短计算时间，但您的解决方案将不准确。 降低您的算法的信心会更快，但获得的解决方案将是不准确的。
• 以下参数适用于此应用程序：
• 以下代码对应于属于PnPProblem类的estimatePoseRANSAC（）函数。 该函数在给定一组2D / 3D对应关系，所需的PnP方法，输出内容容器和Ransac参数的情况下估计旋转和平移矩阵：
• 在下面的代码中是主算法的第3步和第4步。 第一个是调用上面的函数，第二个是从Ransac获取输出内部矢量来获取2D场景点以用于绘图目的。 如代码中所示，如果我们有匹配，我们必须确保应用Ransac，在另一种情况下，由于任何OpenCV错误，函数cv :: solvePnPRansac崩溃。
• 以下代码对应于属于PnPProblem类的backproject3DPoint（）函数。 该函数将在世界参考系中表示的给定3D点反投影到2D图像上：
• 上述函数用于计算对象Mesh的所有3D点以显示对象的姿势。
• 您还可以更改RANSAC参数和PnP方法：
• 线性卡尔曼滤波器用于不良姿态拒绝。
• 在计算机视觉或机器人领域中常见的是，在应用检测或跟踪技术之后，由于一些传感器错误而获得不良结果。 为了避免在本教程中的这些错误检测，解释了如何实现线性卡尔曼滤波器。 在检测到给定数量的内点之后将应用卡尔曼滤波器。
• 在本教程中，它使用基于线性卡尔曼滤波器的cv :: KalmanFilter的OpenCV实现来进行位置和方向跟踪，以设置动态和测量模型。
• 首先，我们必须定义我们的状态向量，它将具有18个状态：位置数据（x，y，z）及其一阶和二阶导数（速度和加速度），然后以三个欧拉角的形式添加旋转（滚动， 俯仰，下颚）及其一阶和二阶导数（角速度和加速度）
• 其次，我们必须定义测量数量为6：从R和t我们可以提取（x，y，z）和（ψ，θ，φ）。 此外，我们必须定义要应用于系统的控制操作的数量，在这种情况下将为零。 最后，我们必须定义测量之间的差分时间，在这种情况下是1 / T，其中T是视频的帧速率。
• 
• 以下代码对应于卡尔曼滤波器初始化。 首先，设置过程噪声，测量噪声和误差协方差矩阵。 其次，设置转移矩阵，即动态模型，最后设置测量矩阵，即测量模型。
• 您可以调整过程和测量噪声，以提高卡尔曼滤波器的性能。 随着测量噪声的降低，在不良测量之前对算法敏感的会更快收敛。

• void initKalmanFilter(cv::KalmanFilter &KF, int nStates, int nMeasurements, int nInputs, double dt)
  {
    KF.init(nStates, nMeasurements, nInputs, CV_64F);                 // init Kalman Filter
    cv::setIdentity(KF.processNoiseCov, cv::Scalar::all(1e-5));       // set process noise
    cv::setIdentity(KF.measurementNoiseCov, cv::Scalar::all(1e-4));   // set measurement noise
    cv::setIdentity(KF.errorCovPost, cv::Scalar::all(1));             // error covariance
                   /* DYNAMIC MODEL */
    //  [1 0 0 dt  0  0 dt2   0   0 0 0 0  0  0  0   0   0   0]
    //  [0 1 0  0 dt  0   0 dt2   0 0 0 0  0  0  0   0   0   0]
    //  [0 0 1  0  0 dt   0   0 dt2 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  1  0  0  dt   0   0 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  1  0   0  dt   0 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  0  1   0   0  dt 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  0  0   1   0   0 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  0  0   0   1   0 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  0  0   0   0   1 0 0 0  0  0  0   0   0   0]
    //  [0 0 0  0  0  0   0   0   0 1 0 0 dt  0  0 dt2   0   0]
    //  [0 0 0  0  0  0   0   0   0 0 1 0  0 dt  0   0 dt2   0]
    //  [0 0 0  0  0  0   0   0   0 0 0 1  0  0 dt   0   0 dt2]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  1  0  0  dt   0   0]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  0  1  0   0  dt   0]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  0  0  1   0   0  dt]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  0  0  0   1   0   0]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  0  0  0   0   1   0]
    //  [0 0 0  0  0  0   0   0   0 0 0 0  0  0  0   0   0   1]
    // position
    KF.transitionMatrix.at(0,3) = dt;
    KF.transitionMatrix.at(1,4) = dt;
    KF.transitionMatrix.at(2,5) = dt;
    KF.transitionMatrix.at(3,6) = dt;
    KF.transitionMatrix.at(4,7) = dt;
    KF.transitionMatrix.at(5,8) = dt;
    KF.transitionMatrix.at(0,6) = 0.5*pow(dt,2);
    KF.transitionMatrix.at(1,7) = 0.5*pow(dt,2);
    KF.transitionMatrix.at(2,8) = 0.5*pow(dt,2);
    // orientation
    KF.transitionMatrix.at(9,12) = dt;
    KF.transitionMatrix.at(10,13) = dt;
    KF.transitionMatrix.at(11,14) = dt;
    KF.transitionMatrix.at(12,15) = dt;
    KF.transitionMatrix.at(13,16) = dt;
    KF.transitionMatrix.at(14,17) = dt;
    KF.transitionMatrix.at(9,15) = 0.5*pow(dt,2);
    KF.transitionMatrix.at(10,16) = 0.5*pow(dt,2);
    KF.transitionMatrix.at(11,17) = 0.5*pow(dt,2);
         /* MEASUREMENT MODEL */
    //  [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
    //  [0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
    //  [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
    //  [0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0]
    //  [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
    //  [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0]
    KF.measurementMatrix.at(0,0) = 1;  // x
    KF.measurementMatrix.at(1,1) = 1;  // y
    KF.measurementMatrix.at(2,2) = 1;  // z
    KF.measurementMatrix.at(3,9) = 1;  // roll
    KF.measurementMatrix.at(4,10) = 1; // pitch
    KF.measurementMatrix.at(5,11) = 1; // yaw
  }

  在下面的代码中是主算法的第5步。 当获得的Ransac之后的内部数量超过阈值时，填充测量矩阵，然后更新卡尔曼滤波器：

• // -- Step 5: Kalman Filter
  // GOOD MEASUREMENT
  if( inliers_idx.rows >= minInliersKalman )
  {
      // Get the measured translation
      cv::Mat translation_measured(3, 1, CV_64F);
      translation_measured = pnp_detection.get_t_matrix();
      // Get the measured rotation
      cv::Mat rotation_measured(3, 3, CV_64F);
      rotation_measured = pnp_detection.get_R_matrix();
      // fill the measurements vector
      fillMeasurements(measurements, translation_measured, rotation_measured);
  }
  // Instantiate estimated translation and rotation
  cv::Mat translation_estimated(3, 1, CV_64F);
  cv::Mat rotation_estimated(3, 3, CV_64F);
  // update the Kalman filter with good measurements
  updateKalmanFilter( KF, measurements,
                translation_estimated, rotation_estimated);

  以下代码对应于fillMeasurements（）函数，该函数将测量的旋转矩阵转换为欧拉角，并将测量矩阵与测量的平移向量一起填充：

  void fillMeasurements( cv::Mat &measurements,
                     const cv::Mat &translation_measured, const cv::Mat &rotation_measured)
  {
      // Convert rotation matrix to euler angles
      cv::Mat measured_eulers(3, 1, CV_64F);
      measured_eulers = rot2euler(rotation_measured);
      // Set measurement to predict
      measurements.at(0) = translation_measured.at(0); // x
      measurements.at(1) = translation_measured.at(1); // y
      measurements.at(2) = translation_measured.at(2); // z
      measurements.at(3) = measured_eulers.at(0);      // roll
      measurements.at(4) = measured_eulers.at(1);      // pitch
      measurements.at(5) = measured_eulers.at(2);      // yaw
  }

   

• 以下代码对应于updateKalmanFilter（）函数，该函数更新卡尔曼滤波器并设置估计的旋转矩阵和平移向量。 估计的旋转矩阵来自估计的欧拉角到旋转矩阵。

  void updateKalmanFilter( cv::KalmanFilter &KF, cv::Mat &measurement,
                       cv::Mat &translation_estimated, cv::Mat &rotation_estimated )
  {
      // First predict, to update the internal statePre variable
      cv::Mat prediction = KF.predict();
      // The "correct" phase that is going to use the predicted value and our measurement
      cv::Mat estimated = KF.correct(measurement);
      // Estimated translation
      translation_estimated.at(0) = estimated.at(0);
      translation_estimated.at(1) = estimated.at(1);
      translation_estimated.at(2) = estimated.at(2);
      // Estimated euler angles
      cv::Mat eulers_estimated(3, 1, CV_64F);
      eulers_estimated.at(0) = estimated.at(9);
      eulers_estimated.at(1) = estimated.at(10);
      eulers_estimated.at(2) = estimated.at(11);
      // Convert estimated quaternion to rotation matrix
      rotation_estimated = euler2rot(eulers_estimated);
  }

   

• 第6步设置估计的旋转平移矩阵：

• 最后一步和可选步骤是绘制找到的姿势。 为此，我实现了一个函数来绘制所有网格3D点和一个额外的参考轴：

• 您还可以修改最小内点来更新卡尔曼滤波器：

效果

以下视频是使用以下参数的解释检测算法实时进行姿势估计的结果：