MATLAB之数值计算

第五部分 数值计算

1.一元函数的极小值点：

由于函数f(x)的最大值为函数-f(x)或1/f(x)的最小值，故利用fminbnd的函数也可以求函数的最大值

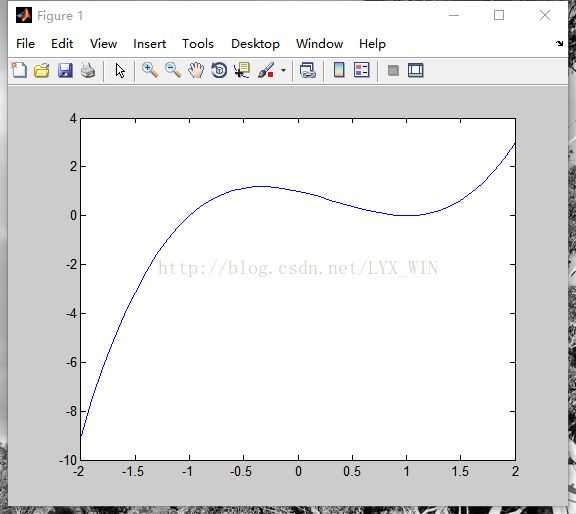
例1：求一元函数在区间[-2,2]的极小值点

>> f=@(x)x.^3-x.^2-x+1;

>> x=fminbnd(f,-2,2)

 

x =

 

    1.0000

 

>> y=f(x)

 

y =

 

   3.5776e-10

画出函数在区间[-2,2]上的图形，也可找到函数在x=1处为极小值点：

 

 

例2：用fminbnd()函数求一元函数在区间[1,3]的极大值

>> f=@(x)-1/5*(x.^4-6*x.^2+8*x+17);  %求极大值的时候加个负号

>> x=fminbnd(f,1,3)

 

x =

 

    3.0000

 

>> y=f(x)

 

y =

 

  -13.5992

2.多元函数的极小值点：

x=fminsearch(fun,x0)  %单纯行下山法求多元函数极值点的指令的最简格式

[x,fval,exitfag,output]=fminsearch(fun,x0,options,p1,p2,...)

%单纯行下山法求多元函数极值点的指令的最完整格式

x=fminunc(fun,x0) %拟牛顿法求多元函数极值点的指令最简格式

[x,fval,exitflag,output,grad,hessian]=fminunc(fun,x0,options,p1,p2,...)

%拟牛顿法求多元函数极值点的指令最完整格式

例：求函数的极小值点

>> y=@(x)100*(x(2)-3*x(1)^2)^2+(1-2*x(1))^2;

>> [x,fval]=fminsearch(y,[-1.2,1])

 

x =

 

    0.5000    0.7500

 

 

fval =

 

   7.2027e-10

3.函数积分

（1）一元函数的数值积分

a.梯形法数值积分

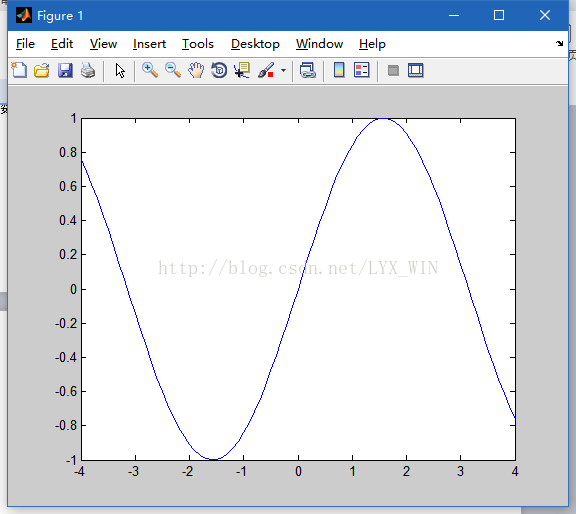
相邻数据间的距离越小，用trap()函数求出来的面积越接近被积函数的真值。自变量之间距离越近，函数值就越接近

例：用梯形法数值积分函数trapz()求的积分

>> x=[-pi:0.1:pi];

>> y=sin(x);

>> area=trapz(x,y)

 

area =

 

   -0.0035

用图形表示：

>> y=sin(x);

>> x=-4:0.1:4;

>> plot(x,y)

 

b.辛普森数值积分

q=quad(‘f(x)’,x1,x2)%表示使用自适应递归的辛普森方法从积分区间[x1,x2]对函数f(x)进行积分，积分的相对误差在1e-3范围内。输入参数中的’f(x)’是一个字符串，表示积分函数的表达式。当输入的是向量时返回值必须是向量形式

q=quad(‘f(x)’,x1,x2,tol)%表示使用自适应递归的辛普森方法从积分区间[x1,x2]对函数f(x)进行积分，积分的误差在tol范围内

q=quad(‘f(x)’,x1,x2,tol,trace) %表示当输入参数trace不为零时，以动态点图的形式实现积分的整个过程，其他同上

q=quad(‘f(x)’,x1,x2,tol,trace,p1,p2...) %表示允许参数p1，p2直接输给函数f(),即g=F(x,p1,p2...)。在这种情况下，当tol和trace使用默认值时，需要输入空矩阵

例：求的积分

>> quad('x.^2+x-5',0,5)

 

ans =

 

   29.1667

c.科茨数值积分：

q=quadl(‘f(x)’,x1,x2)

q=quadl(‘f(x)’,x1,x2,tol)

q=quadl(‘f(x)’,x1,x2,tol,trace)

q=quadl(‘f(x)’,x1,x2,tol,trace,p1,p2...)

例：用科茨积分函数求的积分

>> quadl('exp(-x).*sin(x)',-1,1)

 

ans =

 

   -0.6635

（2）多重数值积分

a.二重积分形式：

具体表示方法：

q=dblquad(fun,xmin,xmax,ymin,ymax)%计算函数在（xxmin,xmax,ymin,ymax）上的二重积分。fun为函数句柄，xin,xmas,ymin和ymax分别表示积分区间的上下界

q=dblquad(fun,xmin,xmax,ymin,ymax，tol)%tol用来指定绝对计算精度

例：使用dblauad()函数在矩形区域内求函数F=ysin(x)+xcos(y)在[pi,2*pi,0,pi]区间的二重积分

>> F=@(x,y)y*sin(x)+x*cos(y);

>> Q=dblquad(F,pi,2*pi,0,pi)

 

Q =

 

   -9.8696

b.三重积分：

triplequad(fun,XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX)   %用来求函数fun(x,y,z)在矩形区间（XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX）上的积分值。函数fun(x,y,z)必须接受向量x及标量y和z并返回一个积分向量

triplequad(fun,XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX，fun)   %使用tol作为允许的误差值，取代默认值1.e-6

例：计算函数 在[0,pi,0,1,-1,1]区间的三重积分

>> F=@(x,y,z)y*sin(x)+z*cos(x);

>> Q=triplequad(F,0,pi,0,1,-1,1)

 

Q =

 

2.0000

4.函数微分

（1）用diff函数求数值微分

调用格式	说明
diff(x)	用来求解向量x的微分，所得值为[x(2)-x(1),x(3)-x(2),...x(n)-x(n-1)]
	用来求解矩阵x的微分，所得值为矩阵的差分[x(2)-x(1),x(3)-x(2),...x(n)-x(n-1)]
	对n维数组求微分，所得值为沿第一个相关维的差分值
diff(x,n)	用来求矩阵的n阶差分值，如果n>size(x,dim),diff()函数先计算肯可能的连续差分值，直到size(x,dim)=1，然后diff()函数沿任意n+1维进行差分计算
diff(x,n,dim)	用来计算n阶差分，如果n>size(x,dim),函数将返回空数组

例：使用diff()函数求解数值微分

>> A=[1 3 5 7 4 9]

 

A =

 

     1     3     5     7     4     9

 

>> diff(A)

 

ans =

 

     2     2     2    -3     5

 

>> B=[1 2 3;5 2 8;9 5 7; 5 1 8]

 

B =

 

     1     2     3

     5     2     8

     9     5     7

     5     1     8

 

>> diff(B)

 

ans =

 

     4     0     5

     4     3    -1

-4    -4     1

5.，常微分方程

（1）常微分方程求解：

[t,y]=solver(odefun,tspan,y0,options)
其中,odefun代表ode()函数的名称，tspan为二元向量[t1,t2]时，定义的是时间求解区间，当表示的是多元向量[t1,t2,t3,...tk],命令会在所定义的时间区间序列中求解，但必须是单序列顺序排列，y0表示微分方程的初始值，options可以来设置，在命令窗口中输入oedset即可。

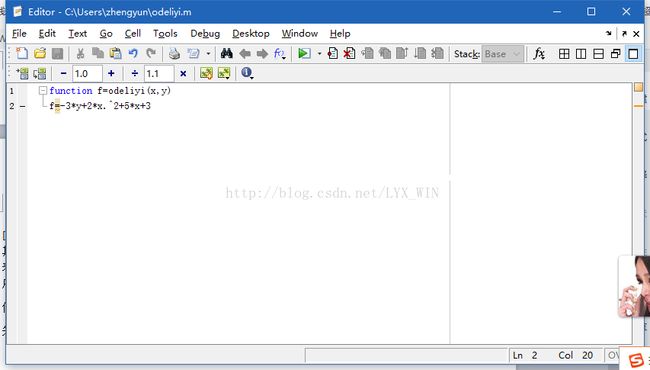
例：求解微分方程

先定义odeliyi函数，文件保存为odeliyi.m,并用debug调试运行下

 

调用定义的odeliyi函数，使用[x,y]=ode23('odeliyi',[1,4],1)对方程进行求解：

x =

 

    1.0000

    1.0114

    1.0686

    1.1719

    1.3015

    1.4641

    1.6715

    1.9415

    2.2415

    2.5415

    2.8415

    3.1415

    3.4415

    3.7415

    4.0000

 

 

y =

 

    1.0000

    1.0792

    1.4539

    2.0563

    2.7141

    3.4446

    4.3025

    5.3919

    6.6446

    7.9868

    9.4374

   11.0034

   12.6878

   14.4915

   16.1429

（2）曲线拟合

polyfit(x,y,n):用最小二乘法对所给数据进行n阶多项式拟合，返回一个拟合多项式f(x)，使得f(x(i))近似等于y(i)

[p,s]=polyfit(x,y,n):运行结果会返回一个多项式，同时返回一个多项式用polyval()函数获得误差分析报告。

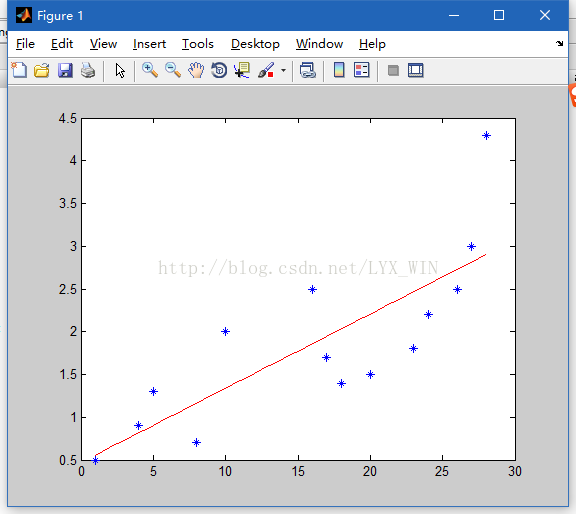
例：用最小二乘法求解拟合

x	1	4	5	8	10	16	17	18	20	23	24	26	27	28
y	0.5	0.9	1.3	0.7	2.0	2.5	1.7	1.4	1.5	1.8	2.2	2.5	3.0	4.3

>> x=[1 4 5 8 10 16 17 18 20 23 24 26 27 28]

 

x =

 

     1     4     5     8    10    16    17    18    20    23    24    26    27    28

 

>> x=[1 4 5 8 10 16 17 18 20 23 24 26 27 28];

>> y=[0.5 0.9 1.3 0.7 2.0 2.5 1.7 1.4 1.5 1.8 2.2 2.5 3.0 4.3];

>> a=polyfit(x,y,1)

 

a =

 

    0.0868    0.4712

 

>> x1=1:0.5:28;

>> y1=a(1)*x1+a(2);

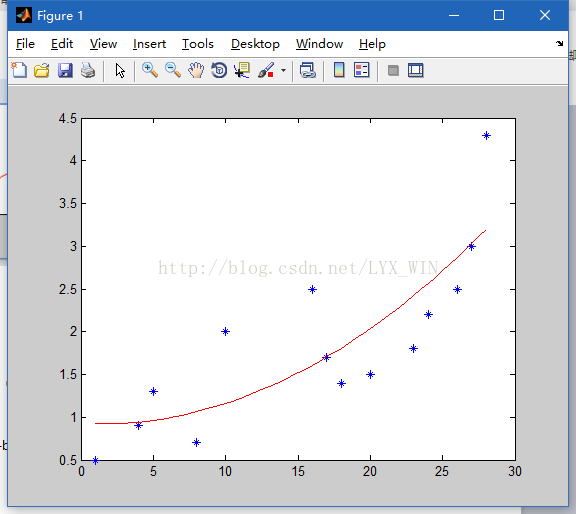
>> plot(x,y,'*',x1,y1,'-r')

 

对上图进行二次拟合：

>> b=polyfit(x,y,2)

 

b =

 

    0.0032   -0.0089    0.9287

 

>> x2=1:0.5:28;

>> y2=b(1)*x2.^2+b(2)*x2+b(3);

>> plot(x,y,'*',x2,y2,'-r')

 

5.多项式及其操作

（1）多项式的表达和创建

例.用poly2sym（）函数构造多项式

>> A=[2 3 7 1 1 3];

>> poly2sym(A)

 

ans =

 

2*x^5 + 3*x^4 + 7*x^3 + x^2 + x + 3

(2)多项式的根

例.求解多项式的根

>> p=[1 0 3 5 2];

>> x=roots(p)

 

x =

 

   0.6585 + 1.9575i

   0.6585 - 1.9575i

  -0.6585 + 0.1878i

  -0.6585 - 0.1878i

(3)导数

用法格式：y=polyder(h)

其中，y为导函数的系数向量，h为原函数的系数向量

例：对多项式求导

 

>> h=[3 5 7 4 2 1 3];

>> y=polyder(h)

 

y =

 

18    25    28    12     4     1

（4）估值

语法格式：y=polyval(p,x)

其中，p代表多项式各阶系数的向量，x代表要求值的点。如果x表示矩阵，需要用y=polyvalm(p,x)来求解对应的值

例1.利用polyval()函数求出在x=7的极值

 

>> p=[5 3 0 5];

>> y=polyval(p,7)

 

y =

 

        1867

例2.利用Polyval()函数求解矩阵多项式  在已知矩阵x处的值，其中x=[1 2 3 ;-1 2 5;-2 3 4].

>> X=[1 2 3 ;-1 2 5;-2 3 4]

 

X =

 

     1     2     3

    -1     2     5

    -2     3     4

 

>> p=[1 5 -3];

>> y=polyvalm(p,X)

 

y =

 

    -5    25    40

   -18    24    52

   -23    29    42

例3.利用polyval()函数求多项式在区间[2,5]均匀分布的5个离散点的值

>> x=[2:5];

>> p=[2 0 3 0 5];

>> y=polyval(p,x)

 

y =

 

          49         194         565        1330

（5）有理多项式

语法格式：[r,p,k]=residue(b,a)

[b,a]=residue(r,p,k)

其中，b表示分子多项式的系数，a表示分母多项式的系数

例.用residue()函数运算多项式

>> b=[3 5 2 9];

>> a=[4 6 0 -5];

>> [r,p,k]=residue(b,a)

 

r =

 

  -0.4020 + 0.9968i

  -0.4020 - 0.9968i

   0.9290          

 

 

p =

 

  -1.1230 + 0.6438i

  -1.1230 - 0.6438i

   0.7460          

 

 

k =

 

    0.7500