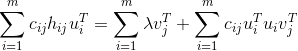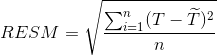Spark MLlib协同过滤之交替最小二乘法ALS原理与实践
请先阅读leboop发布的博文《Apache Mahout之协同过滤原理与实践 》。
基于用户和物品的协同过滤推荐都是建立在一个用户-物品评分矩阵(user-item-score)展开的,其本质是利用现有数据填充矩阵的缺失项(missing entries),也就是预测评分。基于用户的协同过滤通过该评分矩阵来度量用户间的相似度(余弦相似度,距离相似度,皮尔森相似度,皮尔斯曼相似度等等);然后,通过用户间的相似度来寻找被推荐用户u的k-最近邻用户{u1,u2,...,uk};最后,加权{u1,u2,...,uk}给所有物品的评分来预测u尚未评分的每个物品的评分,按预测评分从高到低得到用户u的物品推荐列表{p1,p2,...,ph};现在如果向用户u推荐一个物品,应当推荐p1,如果推荐两个物品,应当推荐p1和p2,以此类推。然而,这个算法并不能很好地适应大规模用户和物品数据,比如亚马逊Amazon数千万用户和数百万物品的在线商城,尽管大多数用户只评分或交易了非常少量的物品,复杂度非常低,但线上环境要求必须在极短的时间内返回结果时,实时计算预测值仍然不可行。为了在不牺牲推荐精准度的情况下在大规模电商网站应用协同过滤推荐算法,人们想到了基于物品的协同过滤推荐,其思想与基于用户协同过滤推荐算法类似,只不过这里使用的是物品间相似度。而这个可以通过离线预计算构建出一个描述所有物品两两间的相似度的物品相似度矩阵。在运行时,如果向用户u推荐物品p,由于物品p的k-最近邻{p1,p2,...,pk}已经通过离线计算好,而且这样的物品数量一般都比较少,所以用他们预测p的评分可以在线上交互应用允许的短时间内完成。
事实上,在《Apache Mahout之协同过滤原理与实践 》一文用到的评分矩阵中,只有一个用户-物品没有评分。一方面,在实际应用中,由于用户只会评价或交易少部分物品,评分矩阵一般都非常稀疏。这种情况下的挑战是用相对少的有效评分得到准确的预测。直接做法就是使用矩阵因子分解从评分模式中抽取出一组潜在的因子(latent factors)并通过这些因子向量描述用户和物品。另一方面,Apache Mahout是使用MapReduce实现基于用户和物品的协同过滤推荐算法,我们知道,MapReduce在集群各计算节点的迭代计算中会产生很多的磁盘文件读写操作,严重影响了算法的执行效率,而Spark MLlib是基于内存的分布式计算框架。所以接下来我们介绍Spark MLlib的协同过滤推荐算法实现细节。
一、显示反馈交替最小二乘法(ALS)
1、矩阵因子分解
例如某个用户-电影/电视剧评分矩阵![]() (m和n表示矩阵的行和列)如下:
(m和n表示矩阵的行和列)如下:
| 用户id/电视剧或电影 | 大头儿子和小头爸爸 | 火影忍者 | 百团大战 | 泰坦尼克号 |
| 1 | 5 | 4 | ? | ? |
| 2 | 4 | 2 | ? | ? |
| 3 | 2 | 5 | 3 | ? |
| 4 | 1 | ? | ? | 4 |
| 5 | ? | ? | 5 | 3 |
我们引入电影/电视剧的4个隐藏特征(latent factors)家庭生活,浪漫爱情,战争历史,剧情曲折,当然这里只是为了说明矩阵分解,可能还有其他隐藏特征。
用户对隐藏特征的偏好矩阵![]() 如下:
如下:
| 用户id/隐藏因子 | 家庭生活 | 浪漫爱情 | 战争历史 | 剧情曲折 |
| 1 | 5 | 1 | 2 | 4 |
| 2 | 4 | 1 | 2 | 2 |
| 3 | 2 | 2 | 3 | 5 |
| 4 | 1 | 4 | 1 | 3 |
| 5 | 2 | 3 | 5 | 3 |
矩阵描述了每个用户对这些隐藏因子的偏好程度,第i个用户的特征向量记作![]() ,
,![]() 是第i个用户对第q个隐藏因子的偏好,比如
是第i个用户对第q个隐藏因子的偏好,比如![]() =(5,1,2,4);
=(5,1,2,4);
电影/电视剧包含隐藏特征的程度矩阵![]() 如下:
如下:
| 电视剧或电影/隐藏因子 | 家庭生活 | 浪漫爱情 | 战争历史 | 剧情曲折 |
| 大头儿子和小头爸爸 | 1 | 0 | 0 | 0 |
| 火影忍者 | 0 | 0 | 0 | 1 |
| 百团大战 | 0 | 0 | 1 | 0 |
| 泰坦尼克号 | 0 | 1 | 0 | 0 |
矩阵描述了电影/电视剧包含隐藏特征的程度,第j个物品的特征向量记作![]() ,其中
,其中![]() 是第j个物品包含隐藏因子q的程度,比如
是第j个物品包含隐藏因子q的程度,比如![]() =(1,0,0,0)。
=(1,0,0,0)。
从上面的这些矩阵我们可以看到,用户1喜欢家庭生活更多,而电视剧《大头儿子和小头爸爸》包含家庭生活特征,所以用户1给这部电视剧的评5分也很高。所以我们可以做如下假设,![]() 矩阵是低秩的(隐藏因子数目k远远小于m和n),用户-物品评分矩阵可以近似等于用户特征矩阵与电影特征矩阵的乘积,如下:
矩阵是低秩的(隐藏因子数目k远远小于m和n),用户-物品评分矩阵可以近似等于用户特征矩阵与电影特征矩阵的乘积,如下:
这种假设是合理的,例如某用户偏好碳酸饮料,而百世可乐、可口可乐、芬达都是含碳酸比较多的饮料,所以可以推断该用户偏好这些饮料。这里碳酸饮料就是一个隐藏因子。所以预测 2、交替最小二乘法(ALS)数学推导 leboop在百度查看了很多关于ALS算法公式的推导,基本都是直接给定结果,但是结果却是错误的,所以这里有必要作为纠正再详细推导一遍。 满足 最小,为了避免过度拟合,引入正则化因子 在上式中 下面我们先来固定 两边对向量 标量C对向量 所以,我们关注第q个分量求偏导,上式继续展开 有 再转回向量,有 类似于一元函数求极值,我们令 有 然后两边转置,有 上面用到了矩阵乘积满足结合律以及矩阵乘积和矩阵转置的关系。有 其中 所以 即 以上以通常多元函数求偏导方法进行的,当然如果你学过矩阵对向量求偏导的知识,可以直接得到这个结果,没必要这样繁琐。 由对称性,得到 如果优化问题变为 我们有 这里 3、算法步骤 (1)初始化参数 首先初始化固定的隐藏因子个数k(根据经验一般选取50~200),参数 (2)计算 将 (3)计算 将 (4)迭代 转向执行第(2)步,直到达到迭代条件(s>=r)或者相邻两次误差小于某个值结束。 二、隐士反馈交替最小二乘法(ALS-WR) 1、数学模型 上面提到显示反馈交替最小二乘法(ALS)适用于解决有明确评分矩阵的应用场景,实际情况,用户没有明确反馈对物品的偏好。我们只能通过用户的某些行为来推断他对物品的偏好,例如用户浏览,收藏,或交易过某个物品,我们可以认为该用户对这个物品可能感兴趣。例如,在用户浏览某个物品中,对该物品的点击次数或者在物品所在页面上的停留时间越长,这时我们可以推用户对该物品偏好程度更高,但是对于没有浏览该物品,可能是由于用户不知道有该物品,我们不能确定的推测用户不喜欢该物品。ALS-WR通过置信度权重c来解决这些问题:对于更确信用户偏好的项赋以较大的权重,对于没有反馈的项,赋以较小的权重。ALS-WR模型的形式化说明如下: 这里 2、公式推导 推导与ALS基本相同,固定 令 有 两边转置,得到 (鉴于本人水平有限,暂证明到此,先粘出很多文章给出的结果,以后有时间证明) 其中 三、Spark MLlib算法实现 1、数据准备 数据格式如下: 第一列为用户id(userId),第二列为物品id(itemId),第三列为用户给物品的评分,转换成用户-物品评分矩阵后,如下: 2、显式反馈 Spark MLlib提供了两种API,一种基于RDD的,在spark.mllib下,该API已经进入维护状态,预计在Spark 3.0中放弃维护,最新的是基于DataFrame,该API在spark.ml下。关于RDD和DataFrame,如果想了解更多,可以参见《Spark DataSet和RDD与DataFrame转换成DataSet》、《Spark DataFrame及RDD与DataSet转换成DataFrame》和《Spark RDD和DataSet与DataFrame转换成RDD》。 (1)基于RDD 推荐代码如下: 程序运行结果: 这里我们可以设置不同的初始参数,那么如何评估哪种结果好些?我们采用如下的均方根误差RESM: T为真实值, 程序如下: 结果如下: (2)基于DataFrame 代码如下: 运行结果如下(中间部分日志已经删除): 3、隐式反馈 与显式反馈基本相同,这里需要使用方法setImplicitPrefs()打开隐式反馈,代码如下: 4、几点问题 (1)冷启动策略 前面当我们使用已经训练好的模型model对测试数据进行预测时,可能会碰到测试数据集中的用户或者物品在训练数据集中从未出现过。这会出现在两种情景中: a、在生产环境中,没有历史评分或者模型尚未训练的新的用户或者物品(这就是冷启动问题) b、在交叉验证中,数据会被分片成训练数据和评估数据。当在Spark的 在Spark中,当用户或者物品在模型中没有出现过,默认会在模型中指定它们的预测值为NaN。这在生产环境中是有用的,因为这表明它是一个新的用户或者物品,然后系统可以使用这个预测做出一个撤退的决策。 然而,在交叉验证中这是不希望的,因为任何NaN的预测值都将导致评估测量中产生NaN(例如,我们程序中使用的RegressionEvaluator),会让模型无法作出选择。当然,Spark允许用户通过设置方法 (2)ALS中参数说明 numBlocks 并行计算的用户或者物品被分块的个数。默认是10 rank 模型中隐藏因子的个数,默认是10 maxIter 程序运行的最大迭代次数,默认是10 regParam ALS中的正则化系数,默认是1.0 implicitPrefs 用来确定使用显示反馈ALS或者调节到隐式反馈(默认是false,使用显式反馈) alpha 用于隐式反馈ALS变量的参数,置信系数,默认是1.0 nonnegative 是否使用非负最小二乘法,默认false (3)Spark中的隐式反馈 spark.ml中的隐式反馈方法来自于![]() k<
k<![]() 矩阵的缺失项就变成了求解
矩阵的缺失项就变成了求解![]() 和
和![]() 。
。![]() k<
k<![]() 有很多,究竟哪个才是最优的?当然使等式成立的肯定是最好的,然而由于推荐系统中数据量非常大且计算复杂度高,或者根本不需要这么精准,所以我们退而求其次,去找到近似解,只要保证
有很多,究竟哪个才是最优的?当然使等式成立的肯定是最好的,然而由于推荐系统中数据量非常大且计算复杂度高,或者根本不需要这么精准,所以我们退而求其次,去找到近似解,只要保证![]() 和
和![]() 的误差在允许的范围之内即可。那么如何度量他们的误差呢?和空间向量距离类似,只不过这里是矩阵,我们计算出两个矩阵中每个项之间的误差,那么使误差之和最小的
的误差在允许的范围之内即可。那么如何度量他们的误差呢?和空间向量距离类似,只不过这里是矩阵,我们计算出两个矩阵中每个项之间的误差,那么使误差之和最小的![]() 和
和![]() 的将是我们需要的。数学表达如下:
的将是我们需要的。数学表达如下:![]() 表示用户i给物品j的评分,也就是评分矩阵
表示用户i给物品j的评分,也就是评分矩阵![]() 的第i行和第j列元素。现在的问题就是求解
的第i行和第j列元素。现在的问题就是求解![]() 和
和![]() 使得
使得![]() ,优化问题变为
,优化问题变为![]() 和
和![]() 都是未知的,
都是未知的,![]() 是
是![]() 的范数,可以简单理解成k维向量的模,也即
的范数,可以简单理解成k维向量的模,也即![]() 。交替最小二乘法的思想就是先固定其中一个,比如固定
。交替最小二乘法的思想就是先固定其中一个,比如固定![]() ,将问题转换成普通的最小二乘法优化问题,求出另外一个
,将问题转换成普通的最小二乘法优化问题,求出另外一个![]() ,然后固定
,然后固定![]() ,再求解
,再求解![]() ,依次交替进行直到满足精度要求或者达到指定的迭代次数,交替最小二乘法也因此而得名,所谓显示反馈是指用户对感兴趣物品有明确的评分,也就是矩阵
,依次交替进行直到满足精度要求或者达到指定的迭代次数,交替最小二乘法也因此而得名,所谓显示反馈是指用户对感兴趣物品有明确的评分,也就是矩阵![]() 是明确的。
是明确的。![]() ,此时上式是关于
,此时上式是关于![]() 的,先将对j求和部分分成两部分,一部分只有j,另一部分是除了j的其他项,如下:
的,先将对j求和部分分成两部分,一部分只有j,另一部分是除了j的其他项,如下:![]() 求偏导,式子的第二、第三和第四部分对于向量
求偏导,式子的第二、第三和第四部分对于向量![]() 是常数,所以实质上只需要对下列式子求偏导即可
是常数,所以实质上只需要对下列式子求偏导即可![]() 的偏导等于标量C对向量的每个分量偏导,即
的偏导等于标量C对向量的每个分量偏导,即![]() 是k阶单位矩阵,因为
是k阶单位矩阵,因为![]() 是
是![]() 的第j列,且
的第j列,且![]()
![]()
![]()
![]()
![]() 或
或![]() 就变成了很多文章中写的
就变成了很多文章中写的![]() 。
。![]() ,迭代总次数r和相邻两次误差C,并随机产生
,迭代总次数r和相邻两次误差C,并随机产生![]() (s=0,表示首次迭代)
(s=0,表示首次迭代)![]()
![]() ,
,![]() 和
和![]() 代入公式
代入公式![]() 得到
得到![]()
![]()
![]() ,
,![]() 和第(2)步计算出的
和第(2)步计算出的![]() 代入公式
代入公式![]() ,得到
,得到![]()
![]()
![]() 并不是明确的评分,可能是点击某个网页的次数或者浏览某个物品的停留时间等等,
并不是明确的评分,可能是点击某个网页的次数或者浏览某个物品的停留时间等等,![]() 是置信度系数。
是置信度系数。![]() ,对
,对![]() 求偏导,有
求偏导,有![]()
![]()
![]() 和
和![]() 都是对角矩阵。
都是对角矩阵。1,101,5.0
1,102,3.0
1,103,2.5
2,101,2.0
2,102,2.5
2,103,5.0
2,104,2.0
3,101,2.5
3,104,4.0
3,105,4.5
3,107,5.0
4,101,5.0
4,103,3.0
4,104,4.5
4,106,4.0
5,101,4.0
5,102,3.0
5,103,2.0
5,104,4.0
5,105,3.5
5,106,4.0
用户id/物品id
101
102
103
104
105
106
107
1
5.0
3.0
2.5
?
?
?
?
2
2.0
2.5
5.0
2.0
?
?
?
3
2.5
?
?
4.0
4.5
?
5.0
4
5.0
?
3.0
4.5
?
4.0
?
5
4.0
3.0
2.0
4.0
3.5
4.0
?
package com.leboop.mllib
import org.apache.spark.mllib.recommendation.{ALS, Rating}
import org.apache.spark.sql.SparkSession
/**
* 基于RDD的ALS API推荐Demo
*/
object ALSCFDemo {
// case class Rating(userId: Int, itermId: Int, rating: Float)
/**
* 解析数据:将数据转换成Rating对象
* @param str
* @return
*/
def parseRating(str: String): Rating = {
val fields = str.split(",")
assert(fields.size == 3)
Rating(fields(0).toInt, fields(1).toInt, fields(2).toFloat)
}
def main(args: Array[String]): Unit = {
//定义切入点
val spark = SparkSession.builder().master("local").appName("ASL-Demo").getOrCreate()
//读取数据,生成RDD并转换成Rating对象
val ratingsRDD = spark.sparkContext.textFile("data/ratingdata.csv").map(parseRating)
//隐藏因子数
val rank=50
//最大迭代次数
val maxIter=10
//正则化因子
val labmda=0.01
//训练模型
val model=ALS.train(ratingsRDD,rank,maxIter,labmda)
//推荐物品数
val proNum=2
//推荐
val r=model.recommendProductsForUsers(proNum)
//打印推荐结果
r.foreach(x=>{
println("用户 "+x._1)
x._2.foreach(x=>{
println(" 推荐物品 "+x.product+", 预测评分 "+x.rating)
println()
}
)
println("===============================")
}
)
}
}
用户 4
推荐物品 101, 预测评分 4.987222374679642
推荐物品 104, 预测评分 4.498410352539908
===============================
用户 1
推荐物品 101, 预测评分 4.9941397937874825
推荐物品 104, 预测评分 4.482759123081623
===============================
用户 3
推荐物品 107, 预测评分 4.9917963612098415
推荐物品 105, 预测评分 4.50190214892064
===============================
用户 5
推荐物品 101, 预测评分 4.023403087402049
推荐物品 104, 预测评分 3.9938240731866506
===============================
用户 2
推荐物品 103, 预测评分 4.985059400785903
推荐物品 102, 预测评分 2.4974442131394214
===============================![]() 和
和![]() 的初始值都是随机产生的,所以每次运行的结果会有差异。从结果中,我们还看到ALS可能会将用户已经评分的物品推荐给该用户,这点与Apache Mahout中基于物品或用户协同过滤不同,例如在用户-物品评分矩阵中用户1已经给物品101评5分,推荐结果中也将结果推荐给了他,预测评分4.98非常接近真实值。
的初始值都是随机产生的,所以每次运行的结果会有差异。从结果中,我们还看到ALS可能会将用户已经评分的物品推荐给该用户,这点与Apache Mahout中基于物品或用户协同过滤不同,例如在用户-物品评分矩阵中用户1已经给物品101评5分,推荐结果中也将结果推荐给了他,预测评分4.98非常接近真实值。![]() 为预测值。
为预测值。package com.leboop.mllib
import com.leboop.mllib.ALSCFDemo.rems
import org.apache.spark.mllib.recommendation.{ALS, MatrixFactorizationModel, Rating}
import org.apache.spark.rdd.RDD
import org.apache.spark.sql.SparkSession
/**
* 基于RDD的ALS API推荐Demo
*/
object ALSCFDemo {
/**
* 解析数据:将数据转换成Rating对象
*
* @param str
* @return
*/
def parseRating(str: String): Rating = {
val fields = str.split(",")
assert(fields.size == 3)
Rating(fields(0).toInt, fields(1).toInt, fields(2).toFloat)
}
/**
* @param model 训练好的模型
* @param data 真实数据
* @param n 数据个数
* @return 误差
*/
def rems(model: MatrixFactorizationModel, data: RDD[Rating], n: Long): Double = {
//预测值 Rating(userId,itermId,rating)
val preRDD: RDD[Rating] = model.predict(data.map(d => (d.user, d.product)))
//关联:组成(预测评分,真实评分)
val doubleRating = preRDD.map(
x => ((x.user, x.product), x.rating)
).join(
data.map { x => ((x.user, x.product), x.rating) }
).values
//计算RMES
math.sqrt(doubleRating.map(x => math.pow(x._1 - x._2, 2)).reduce(_ + _) / n)
}
def main(args: Array[String]): Unit = {
//定义切入点
val spark = SparkSession.builder().master("local").appName("ASL-Demo").getOrCreate()
//读取数据,生成RDD并转换成Rating对象
val ratingsRDD = spark.sparkContext.textFile("data/ratingdata.csv").map(parseRating)
//将数据随机分成训练数据和测试数据(权重分别为0.8和0.2)
val Array(training, test) = ratingsRDD.randomSplit(Array(1, 0))
//隐藏因子数
val rank = 50
//最大迭代次数
val maxIter = 10
//正则化因子
val labmda = 0.01
//训练模型
val model = ALS.train(training, rank, maxIter, labmda)
//计算误差
val remsValue = rems(model, ratingsRDD, ratingsRDD.count)
println("误差: " + remsValue)
}
}
误差: 0.011343969370562474package com.leboop.mllib
import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.ml.recommendation.ALS
import org.apache.spark.sql.SparkSession
/**
* ASL基于DataFrame的Demo
*/
object ALSDFDemo {
case class Rating(userId: Int, itemId: Int, rating: Float)
/**
* 解析数据:将数据转换成Rating对象
* @param str
* @return
*/
def parseRating(str: String): Rating = {
val fields = str.split(",")
assert(fields.size == 3)
Rating(fields(0).toInt, fields(1).toInt, fields(2).toFloat)
}
def main(args: Array[String]): Unit = {
//定义切入点
val spark = SparkSession.builder().master("local").appName("ASL-DF-Demo").getOrCreate()
//读取数据,生成RDD并转换成Rating对象
import spark.implicits._
val ratingsDF = spark.sparkContext.textFile("data/ratingdata.csv").map(parseRating).toDF()
//将数据随机分成训练数据和测试数据(权重分别为0.8和0.2)
val Array(training, test) = ratingsDF.randomSplit(Array(0.8, 0.2))
//定义ALS,参数初始化
val als = new ALS().setRank(50)
.setMaxIter(10)
.setRegParam(0.01)
.setUserCol("userId")
.setItemCol("itemId")
.setRatingCol("rating")
//训练模型
val model = als.fit(training)
//推荐:每个用户推荐2个物品
val r = model.recommendForAllUsers(2)
//关闭冷启动(防止计算误差不产生NaN)
model.setColdStartStrategy("drop")
//预测测试数据
val predictions = model.transform(test)
//定义rmse误差计算器
val evaluator = new RegressionEvaluator()
.setMetricName("rmse")
.setLabelCol("rating")
.setPredictionCol("prediction")
//计算误差
val rmse = evaluator.evaluate(predictions)
//打印训练数据
training.foreach(x=>println("训练数据: "+x))
//打印测试数据
test.foreach(x=>println("测试数据: "+x))
//打印推荐结果
r.foreach(x=>print("用户 "+x(0)+" ,推荐物品 "+x(1)))
//打印预测结果
predictions.foreach(x=>print("预测结果: "+x))
//输出误差
println(s"Root-mean-square error = $rmse")
}
}
训练数据: [1,101,5.0]
训练数据: [1,102,3.0]
训练数据: [1,103,2.5]
训练数据: [2,101,2.0]
训练数据: [2,102,2.5]
训练数据: [2,104,2.0]
训练数据: [3,101,2.5]
训练数据: [3,105,4.5]
训练数据: [3,107,5.0]
训练数据: [4,101,5.0]
训练数据: [4,103,3.0]
训练数据: [4,104,4.5]
训练数据: [4,106,4.0]
训练数据: [5,102,3.0]
训练数据: [5,103,2.0]
训练数据: [5,104,4.0]
训练数据: [5,105,3.5]
测试数据: [2,103,5.0]
测试数据: [3,104,4.0]
测试数据: [5,101,4.0]
测试数据: [5,106,4.0]
用户 1 ,推荐物品 WrappedArray([101,4.98618], [105,3.477826])
用户 3 ,推荐物品 WrappedArray([107,4.9931526], [105,4.499714])
用户 5 ,推荐物品 WrappedArray([104,3.9853115], [105,3.4996033])
用户 4 ,推荐物品 WrappedArray([101,5.000056], [104,4.5001974])
用户 2 ,推荐物品 WrappedArray([105,3.0707152], [102,2.4903712])
预测结果: [5,101,4.0,3.1271331]
预测结果: [2,103,5.0,1.0486442]
预测结果: [5,106,4.0,1.8420099]
预测结果: [3,104,4.0,1.4847627]
Root-mean-square error = 2.615265256309832val als = new ALS()
.setMaxIter(5)
.setRegParam(0.01)
.setImplicitPrefs(true)
.setUserCol("userId")
.setItemCol("movieId")
.setRatingCol("rating")CrossValidator 和TrainValidationSplit中使用简单的随机分片时,碰到评估数据集中的用户或者物品没有出现在训练数据集中是非常普遍的。coldStartStrategy 的参数为“drop”来删除预测结果中含有NaN的任何DataFrame行,这样,评估度量可以在非NaN的数据上进行计算变得有效。Collaborative Filtering for Implicit Feedback Datasets

![C=\sum_{i=1}^{m}\sum_{j=1}^{n}[(a_{ij}-u_{i}v_{j}^{T})^2+\lambda (\left \|u_{i} \right \|^{2}+\left \| v_{j} \right \|^{2})]](http://img.e-com-net.com/image/info8/1f2482492bce41d58c5d945f56b6f9ea.gif)
![C=\sum_{i=1}^{m}[(a_{ij}-u_{i}v_{j}^{T})^2+\sum_{p\neq j}(a_{ip}-u_{i}v_{p}^{T})^2+\lambda nu_{i}u_{i}^{T}+\lambda\sum_{p\neq j} v_{p}v_{p}^{T}+\lambda v_{j}v_{j}^{T}]](http://img.e-com-net.com/image/info8/e4ac40a06b404c7cbdf856cb1e2e0e61.gif)
![\sum_{i=1}^{m}[(a_{ij}-u_{i}v_{j}^{T})^2+\lambda v_{j}v_{j}^{T}]](http://img.e-com-net.com/image/info8/3a2387ad63174e17a3b30d07936b9c5a.gif)
![\sum_{i=1}^{m}[(a_{ij}-\sum_{p=1}^{k} u_{ip}v_{jp})^2+\lambda \sum_{p=1}^{k} v_{jp}^{2}]](http://img.e-com-net.com/image/info8/bd344ac7d2154225bbd7b27568a84ae8.gif)


![\sum_{i=1}^{m}a_{ij}u_{i}^{T}=[\sum_{i=1}^{m}(\lambda E_{k\times k}+u_{i}^{T}u_{i})]v_{j}^{T}\\](http://img.e-com-net.com/image/info8/60e77beca6eb46b8b361f9988bd65ee9.gif)
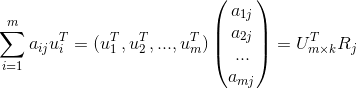
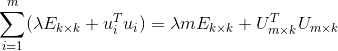
![min[\sum_{i=1}^{m}\sum_{j=1}^{n}(a_{ij}-u_{i}v_{j}^{T})^2+\lambda (\sum_{i=1}^{m}\left \|u_{i} \right \|^{2}+\sum_{j=1}^{n}\left \| v_{j} \right \|^{2})]](http://img.e-com-net.com/image/info8/34b8767008d349d78fe39eed2513fc4e.gif)
![min\sum_{i=1}^{m}\sum_{j=1}^{n}[c_{ij}(h_{ij}-u_{i}v_{j}^{T})^2+\lambda (\left \|u_{i} \right \|^{2}+\left \| v_{j} \right \|^{2})]](http://img.e-com-net.com/image/info8/0082e1f603484e6f930a1fd3cd4f352c.gif)