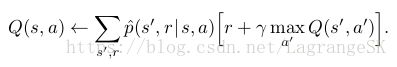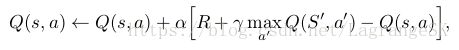强化学习系列（八）：Planning and learning with Tabular Methods（规划和离散学习方法）

一、前言

本章是对前面七章的一个总结归纳，前七章中我们首先介绍马尔科夫决策过程（MDP），而后介绍了求解环境模型已知的MDP的方法（model-based)——动态规划方法（DP)，启发式搜索也属于这类方法。最后针对环境模型未知(model free)的MDP，介绍了基于学习的强化学习方法——蒙特卡罗（MC）、时间差分（TD）等。前七章重点讨论了这两类方法的区别，但这两类方法也有以下共同点：

• 方法的核心都是计算value function
• 都是站在当前state，向前看，然后计算backup value
• 用backup value来更新value function 的估计值

在第七章，我们介绍了一种介于MC和TD之间的算法，本章旨在说明model-based和model-free方法之间的联系，并介绍他们的融合思路。

二、Model和Planning

首先我们进行一组概念辨析：

2.1 model

---

Model

什么是model? agent用model来预测环境对action的反应。根据包含信息的不同，可以分为 distribution model （分布模型）和 sample model（采样模型）。两者区别如下：

• distribution model produce a description of all possibilities and their probabilities. Sample model produce just one of the possibilities and their probabilities.
• 当给定一个state和一个action时，distribution model 可以生成所有可能的状态转移，而sample model只能给出一个可能的状态转移
• 当给定一个state和Policy时，distribution model 可以获得所有可能的episode并得到他们出现的概率，但sample model只能给出一个episode

总之，distribution model 比 sample model包含更多信息，但现实中往往更容易获得sample model。简单来说，distribution model 包含了所有状态的转移概率，但sample model更像是管中窥豹，可见一斑。在DP中，我们用到的是distribution model，而在MC中我们用到的是sample model。

model 是对环境的一种表达方式，（不一定是真实或完全正确的），可以用来产生仿真经验（simulation experience）。

---

2.2 Planning

---

Planning

从Model中生成或提升Policy 的计算过程称为 Planning：

注意本文讨论的Planning都是state space Planning，这种Planning有两个特点：

• 通过计算values function 来进行Policy 提升
• 根据simulated experience来计算value function

---

总体过程可以用下图表示：

根据前七章的介绍，Planning（如DP） 和learning（如MC、TD）方法的核心都是用backing-up 更新公式计算value function 的估计值。区别在于Planning 所用经验是有模型生成的simulated exprience，而learning method使用的经验是由真实环境生成的real exprience。
但两者都满足上述state space Planning结构，这表示很多思想和算法可以相互借鉴，在应用中常常用learning 中value function 估计值的更新公式取代Planning中的value function 估计值的更新公式。例如，我们可以将Q learning 和 planning 结合，得到random-sample one-step tabular Q-planning 方法：

one-step tabular Q-learning最终会收敛到一个对应于真实环境的optimal Policy，而 random-sample one-step tabular Q-planning 则收敛到一个对应于model 的optimal Policy。

Q-planning表示Planning 结合learning 后可以单步更新，计算量显著减小，接下来将详细介绍Planning 和learning 的结合细节。

三、Dyna： Integrating Planning，Acting，and learning

进行在线规划（on-line planning), 与环境交互时，引发了一系列问题：交互过程中所获得的新信息可能会改变之前用于Planning 的 model，从而对Planning产生影响。

3.1 Dyna-Q

通常会根据当前或未来的 states 和 decisions来描述 Planning过程，当decision making（决策）和 model learning（模型学习，用来不断完善model，使得和真实环境更接近）都很消耗计算资源时，为了计算资源分配，常常将二者分开讨论，为了探索这一问题，本节提出了一种on-policy Planning agent的简单结构——Dyna-Q:

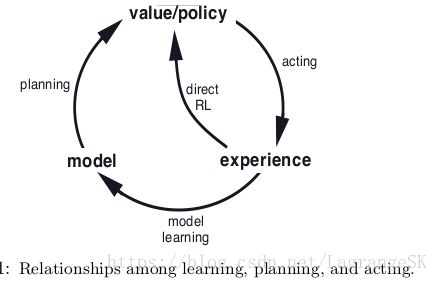
在Planning agent中，对所获得的真实环境信息来说，至少有两个主线任务：

• model learning：将真实经验用于提高模型精确度，使得model更接近真实环境
• direct RL(Reinforcement learning): 对真实经验数据运用强化学习来提升value function 和Policy

Dyna-Q 依次包括了Planning, acting, model learning, direct RL 等过程。其中，Planning方法为上文提到的random-sample one-step tabular Q-planning，direct RL方法为 one-step tabular Q-learning，model learning也是一种 table-based 方法，且假设环境是确定性的（即当前状态 St S t ，采取动作 At A t ，一定会转移到下一时刻状态 St+1 S t + 1 并获得 Rt+1 R t + 1 ), 在model 中可以查阅的state-action pairs必须是有历史信息的。

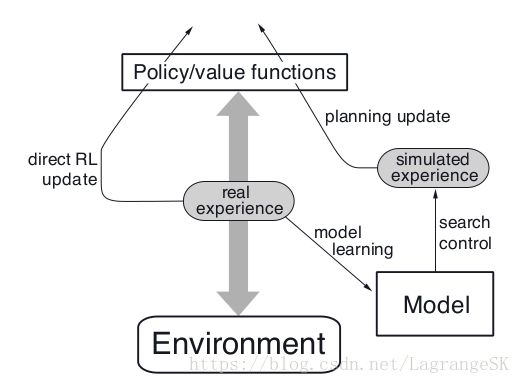
3.2 Dyna

从特殊到一般，Dyna agents的一般结构如下：

其中，中轴线为agent与环境交互的过程，会生成一系列的 real expericence，左侧direct RL 利用 real expericence 提升 value function 和Policy。右侧，model learning 利用 real expericence 来对环境建模生成model，search control 表示从model中选择 starting states和 actions来生成的simulated experience 的过程，最后，Planning 对simulated experience 运用强化学习方法。

在Dyna-Q中，one-step Q-learning分别被用于 learning 和Planning ，区别在于learning （此处为direct RL）中one-step Q-learning的作用对象为 real experience, 而在Planning 中，one-step Q-planning的作用对象为 simulated experience。

从概念上而言，Planning, acting, model learning, direct RL应该是同步进行的，但在实际运用中，acting, model learning, direct RL所占用的计算资源远小于Planning，所以调整了他们是执行顺序，先执行acting, model learning, direct RL，再进行几步Planning，以Dyna-Q为例，算法伪代码如下：

其中direct RL，model learning, Planning分别对应的步骤为（d),(e)和 (f)，如果去掉(e)和 (f) ，那么就变成了一个 one-step tabular Q-learning。

下面以一个小例子简单说明一下Dyna-Q和单纯的one-step Q-learning的区别。

---

Dyna-Maze

走迷宫：阴影部分表示障碍物，和迷宫边界一样，撞到就相当于在原地不动，到达目标（G)时，reward=1，其他时候均为0，到达目标后回到起始位置（S)开始下一个episode，actions={up,down,right,left}，折扣系数为 γ=0.95 γ = 0.95 ，学习率为 α=0.1 α = 0.1 , 探索率为 ϵ=0.1 ϵ = 0.1 , 其中 agent会进行 n步Planning，当n=0时为单纯的one-step Q-learning。结果如图。

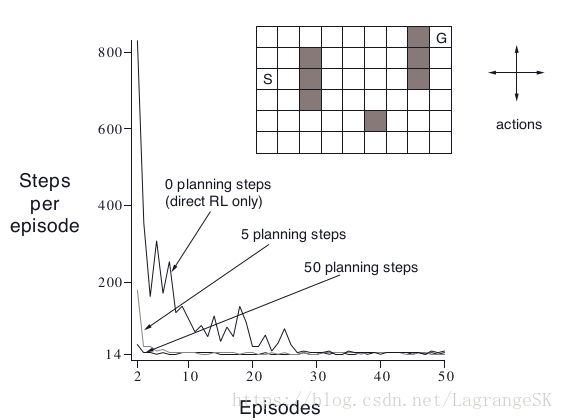
没有planning的方法需要25次收敛，有5次planning方法需要5次收敛，有50次的planning方法只需要3次就收敛啦！为什么呢？

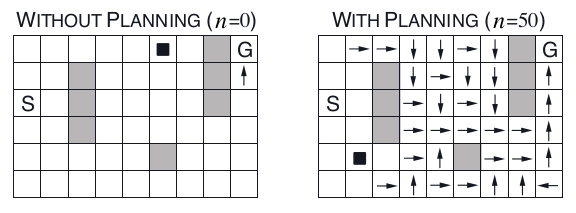
对0次planning 和 50次planning进行比较，当第二个episode时，0次planning的方法只对最靠近目标的动作进行了更新，但50次planning的方法会从目标（G) 回溯到初始状态（S）附近。

---

Planning 和 learning在 Dyna-Q中相辅相成，model learning 不断调整 model 以获得更精确的Planning，而learning 不断提升value和 Policy，两者叠加，加速了算法是收敛速度。

四、When the Model Is Wrong

前一小节提到的迷宫小例子，环境是改变是适度的，即随着小人位置的移动，他所看到的环境有一定的变化，但是总体环境没有改变。但在现实生活中，我们不可能总那么幸运，根据当前环境信息构建的Model很可能是不正确的，原因如下：

• 环境是随机的，且仅仅有一部分数据可以被观测到
• 用function approximate（函数逼近）学到的model不完美
• 环境在变化，新的行为没有被检测到

当model 不正确时，Planning 往往会陷入局部最优。

4.1 容易被发现的模型错误

在一些情况下，Planning计算出的局部最优策略会很快引导我们发现model 的错误。通常，这些情况下，原有的最优策略失效，有些 state 可能无法到达，下面举个例子详细说明这类情况。

---

Blocking Maze:
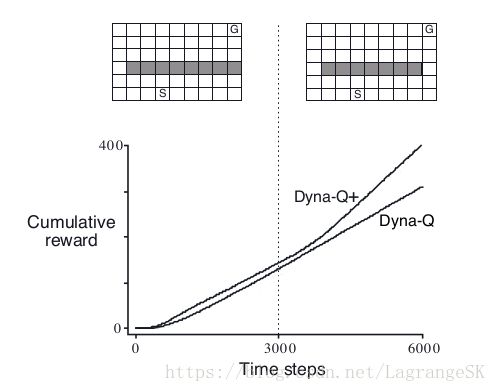
初始时刻的环境左图所示，最短路径是贴着右侧边缘行走，到1000步之后，环境变为右图，最短路径为贴着左侧边缘行走，而原来的最优策略无法通行。实验结果表明，Dyna-Q和Dyna-Q+（稍后详细说明）都可以在1000步以内找到最优策略，但1000步后环境发生变化，他们的return保持不变，一段时间后，return继续增加，表明Dyna-Q和Dyna-Q+发现了model的错误，并找到了新的最优策略。

---

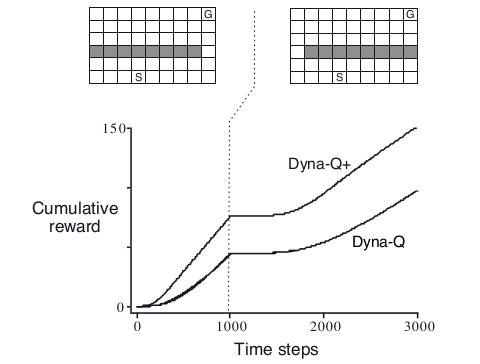
4.2 不容易被发现的模型错误

但是当环境中原始最优策略可以通行，环境整体变得更好，出现更好的策略时，model错误在短时间内变得不容易被发现。我们来看下一个例子。

---

Shortcut Maze
初始时刻环境如左图所示，最优策略为沿着左侧行走，3000步后，环境发生变化，原始最优策略的路径仍然可以通行，在此基础上开辟了一条新的路径，比原始最优路径好。但是实验结果显示 Dyna-Q的return曲线没有明显的波折，表明 Dyna-Q并没有发现model的错误。

---

这里在Planning 中，也存在了另一种意义上的 exploration 和 exploitation矛盾。 exploration 表示希望尝试更多的action 来提高model的准确度， exploitation表示希望在现有model中找到最优Policy。我们一方面希望足够的探索，来发现环境，另一方面，希望探索不要过大，以防止降低方法的性能。在之前提到的解决exploration 和 exploitation矛盾的方法中，不并总是完美和实用，本节将介绍一种简单的启发式算法，可以很有效的平衡exploration 和 exploitation。

4.3 Dyna-Q+

Dyna-Q+在Dyna-Q的基础上，对每组state-action 距离自身最近一次出现的消失时间进行了统计，然后认为消失时间越久的state-action越容易发生变化，他的model就越可能出错。

为了鼓励算法去探索那些长时间没有尝试的action，定义一个bonus reward：如果model的reward 为 r, 一组state-action 有 τ τ 个时间没有出现，那么这组state-action 的reward为 r+kτ√ r + k τ 。其中，k为一个较小的系数。在shortcut maze中，Dyna-Q+的表现比Dyna-Q 好。

五、Prioritized Sweeping (优先扫描）

5.1 backward focusing

在Dyna中，仿真数据由一系列随机均匀选取的初始state-action产生，但对所有state-action等概率的选择不是最好的，有重点地关注一些state-action会更好。举个例子，在第三节的Dyna-Maze图中，

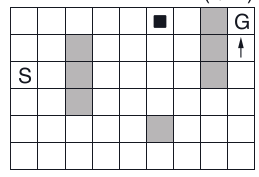
第二个episode开始时，只有指向且最靠近目标（G)（箭头位置）的state-action的value为正值，其余state-action的value都是0。此时，更新大部分的state-action的values都毫无意义，根据下式，不过是从0到0，毫无变化。只有更新可以指向目标状态的state-action value才有意义。

如果每个state-action的更新概率是均等的，将会在更新state-action value 有变化的state-action之前，浪费很多不必要的时间（用于从0到0的无意义更新）。当state space足够大时，会浪费更多的时间，因此，找到一个有侧重的更新方式很有必要。

上述例子表示，最好重点更新从目标状态（goal state) 向后追溯的state-action。但目标状态是一个特定的状态，而我们希望获得一个普适的方法，在任意value有变化的 state 下，都能找到我们需要重点关注并更新的 state-action。

假设，所有value被正确初始化，假设此时agent发现了environment的一点变化，并改变了一个state的 value 估计值。这意味着很多state的value也发生了改变，但是有效的单步更新依赖于那些直接到达该state的action，如果这些action更新了，那么前一步的states的values也可能发生变化。
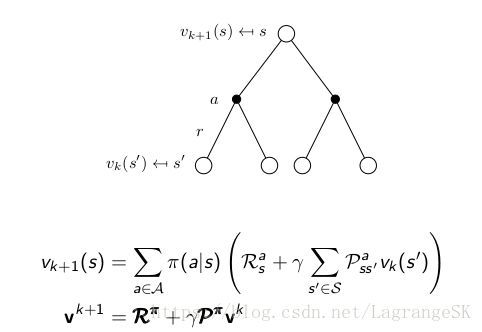
上述过程可以看成Policy evaluation 的逆向过程，根据

可知，如果一个 vk(s′) v k ( s ′ ) 发生变化，那么 vk+1(s) v k + 1 ( s ) 发生变化，此时就是从s‘追溯到s的过程。（虽然图中，s为一个单一state，但如迷宫问题，s可能是多个不同的state，而 actions 就是从这些 s 到达状态 s’对应的动作）。这样，就可以根据任意value有变化的state向前回溯。这就是backward focusing 思想。

5.2 prioritized sweeping

根据上述backward focusing 思想可以反向传播获得一系列的state - action，但不是每个state - action都一样有用，一些state 的value改变比较频繁，而另一些改变比较小。 value变化较大的state-action 之前的state-action的value变化大的可能性较高。在随机环境中，变化的可能性与变化程度和state-action需要被更新的紧急程度有关。根据紧急程度进行优先性排序，这是优先扫描（prioritized sweeping)的基本思想。

用一个队列存储每个value变化较大的state-action，按照变化程度进行排序，当顶端的state-action被更新时，计算这个state-action的前任state-action们的变化，如果变化超过某个阈值，则将这些前任state-action们插入队列，并重新排序队列，与此循环，直到队列元素全部清出，上述整个算法用于确定性环境（deterministic environment）的伪代码如下：

刚刚介绍了确定性环境下的prioritized sweeping，接下来将prioritized sweeping思想扩展到不确定环境下。通过不断统计每个state-action的出现次数，和下一步所有可能出现的state-action构成了model，用expected update(期望更新）取代一个 sample update(采样更新），计算所有可能的下一步的states和他们出现的概率。

prioritized sweeping只是提高规划效率的一种方法，但不是最好的方法。将其扩展到不确定环境下，便受到了期望值的限制，会浪费很多时间在计算低概率的转移上。在下一节中，我们将说到：在很多情况下，采样更新（sample updates）明显减小了计算量，其结果很接近真实的value function。

backward focusing只是一种侧重更新思想，还有很多其他的侧重更新方法，例如forward focusing侧重在当前Policy下经常出现的states容易到达下一步的states。

六、Expected vs. Sample Updates

在前面几节中介绍了Planning和learning 方法的结合点，在本章剩下章节中，我们重点分析一些Planning和learning 方法结合的思想，从Expected 和 Sample Updates开始。
迄今为止，我们讨论过的方法都可以归结为对value-function的更新。针对one-step updates可以将问题分为三个维度：

• 第一，是更新state value 还是更新action value，
• 第二，更新一个任意Policy 下的value 还是更新optimal Policy下的value。
• 第三，是采用expected 更新，考虑所有可能发生的事件，还是sample 更新，考虑一个采用中可能发生的事件。

这三个维度组成八个基本情况：

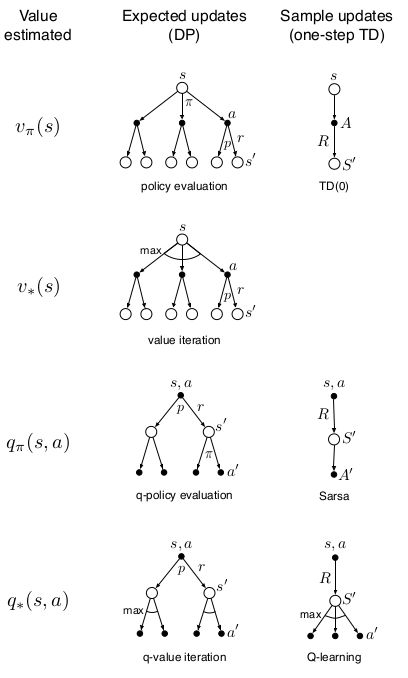
在第六章中，我们介绍了one-step sample updates,对更新 action value而言，和expected updates的区别如下：

---

expected updates

sample updates

---

expected update的计算量比较大，而sample update的计算量比较小，但是sample update真的可以接近expected update吗？这里直接给出结论：

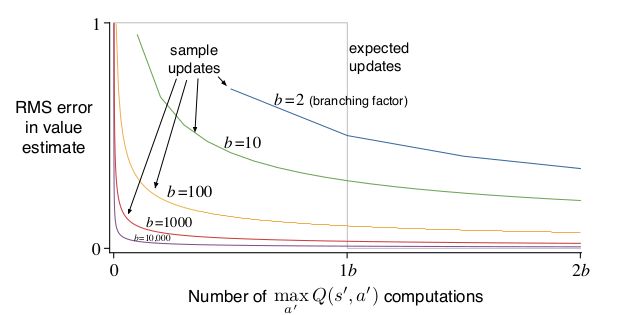
- 在大的随机branching factor，且state过多的情况下，sample updates比 expected update效果好。

七、Trajectory sample

本节将比较两种分布更新方式：

• Exhaustive sweep 在DP（动态规划）中，扫描所有的state（或state-action)，每次扫描更新一次所有的state（或state-action)。当state过多时，单次扫描的时间消耗过大。在很多任务中，很多state之间是没啥关系的，全部扫描意味着每个state都需要消耗同样的时间，不如重点关注某些需要的state，而忽视那些无关的state。
• 根据某些分布来从state 或者state-action space中进行采样。 Dyna-Q的agent 使用了均匀采样（uniform) ，但这会导致和 Exhaustive sweep 相同的一些问题，更常用的是根据 on-policy 分布进行采样，即根据当前策略（current policy） 所观测到的分布。在current policy下与model交互时，很容易就能获得该分布。在episode 问题中，从初始state出发，根据current policy，可以生成一条到terminal state 的采样数据。连续问题中，从初始state开始，可以根据current policy ，一直生成采样数据。在这两类问题中，采样数据的state转移和reward都由model提供，而采样action由当前策略（current policy）给出。这种生成采样数据的方式叫做 trajectory sample。

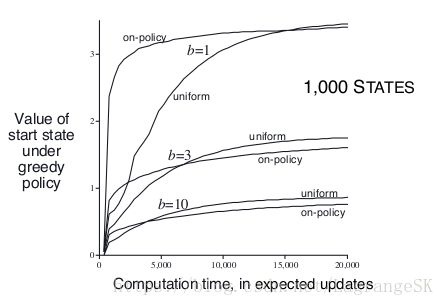
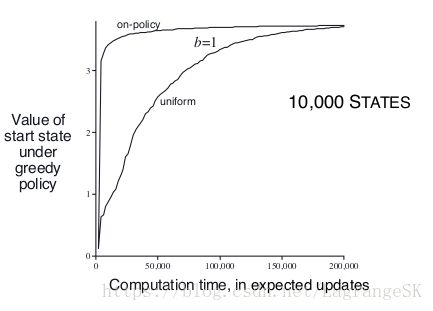
利用on-policy分布的好处是忽略了大部分没有意义的state,但是会让一部分state space一直被更新。比较on-policy分布和uniform分布的效果。在uniform实验中，我们循环遍历每组state-action，并依次更新每组state-action。在on-policy实验中，我们模拟出一些episodes：他们的初始state相同，更新那些在 ϵ ϵ -greedy 策略下出现的state-action。假设一个state对应b个可以到达的下一时刻的state，b被称作branching factor，实验结果如下：

由图可知，短时间内，以on-policy 分布进行采样可以重点关注邻近初始state 的子状态。在states越多，branching factor越小的情况下, 以on-policy 分布的采样的影响越明显且长远。长期看来，以on-policy 分布进行采样是不好的，因为经常出现的states都有了准确的value，不需要再估计了，对他们进行采样没有意义。

对大型问题来说，以on-policy 分布进行采样表现较好，尤其是state-action space中只有一小部分的state-action 在on-policy分布下出现时。

八、Real-time Dynamic Programming

Real-time Dynamic Programming简写为RTDP，是一种 on-policy trajectory-sampling 的异步动态规划value iteration 算法。异步动态规划算法不需要依次扫描state space，可以以任意顺序更新state value，与第四章中介绍的传统DP方法相比，RTDP的更新顺序由真实或仿真trajectories （state action reward序列）中的出现的state次序决定。

如果这些trajectories的起始状态（start state）为一个小子集，即只能从特定的state集合中选取start state。

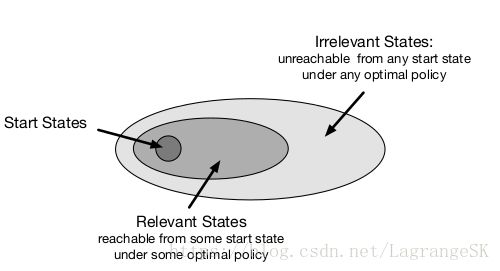
• 对于 prediction 问题（对于一个给定Policy，需要估计出当前的value ），on-Policy trajectory sampling允许算法彻底跳过一些在start state集合下采用当前策略不可能到达的states，这些到不了的state和prediction 问题关系不大。

• 对于control 问题（需要找到一个optimal Policy，而不是估计当前策略的value)，同样有一些在start state集合下采用optimal Policy也无法到达的states,这些states和optimal Policy无关，因此可以不在意这些states对应什么action。此时，我们需要找到是一个optimal partial policy，即局部最优策略，即对于与optimal Policy有关的states是最优策略，但对与optimal Policy无关的states而言，可以随便选择action，甚至可以不选。如上图所示。

on-Policy trajectory-sampling control 方法 Sarsa 需要在 exploring starts 前提下无限次遍历所有的 state-action才能找到optimal policy，RTDP也是如此。但对于某类问题RTDP可以很快找到optimal partial policy，不需要无限次遍历和optimal Policy有关的states，甚至可以永远不经过其中某些states。这类问题需要满足条件如下：

• the initial value of every goal state is zero,
• there exists at least one policy that guarantees that a goal state will be reached with probability one from any start state,
• all rewards for transitions from non-goal states are strictly
• all the initial values are equal to, or greater than, their optimal values (which can be satisfied by simply setting the initial values of all states to zero).

总之，RTDP相比传统DP方法而言，是一种关注局部有效state从而提升算效率的算法。

九、Planning at Decision Time

这里介绍两类Planning：

• background Planning 一种是我们前面一直在说的基于model产生的simulated experience用以逐步提升Policy 或 value function的Planning。通过比较当前state下的value，来选择action。在当前state下，选择action之前，Planning重点在于提高value表或者value 的近似函数表达，涉及到为很多state选择action。此处，Planning所关注的不是当前state。
• decision-time Planning 每给出一个新的state就立即规划出一个action，这种Planning方式比one-step-ahead 方式更深入。通常这种Planning方式多用在不需要快速回应的任务中，如下象棋，可以允许有一定的决策时间。

十、Heuristic Search（启发式搜索）

人工智能中基于的state-space planning的传统decision-time Planning方法统称为heuristic search。

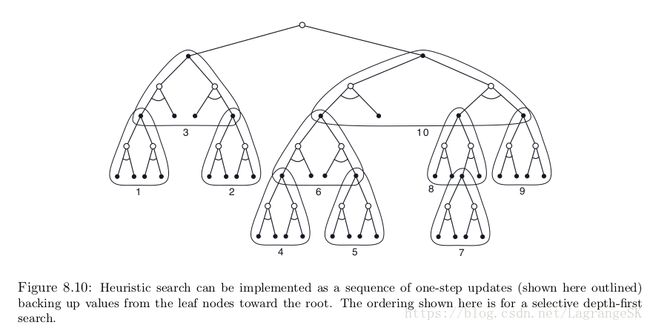
对每个出现的state，都需要考虑一个树状结构，从叶节点开始估计value function，然后回到current state（根节点），如果说，之前介绍的是one-step-ahead的DP 方法，这个就是向前看多步，然后来估计当前节点的value function。当根据计算的value function选择出当前action时，所有的backup values都被丢弃，不用存起来。

heuristic search的特点在与着眼于当前状态（current state）和当前动作（current action），以树状结构进行深层搜索，利用backup思想，来估计当前state的value function，从而选择action。

总的来说，在估计当前value function时，往前看很多步比one-step ahead 的方法要准确。

十一、Rollout Algorithms

Rollout 算法是基于Monte Carlo control的decision-time Planning方法，用到的都是从当前state出发的simulated trajectories数据。

和Monte Carlo control方法不同，rollout 算法的目标不是为了估计最优的action-value function q∗ q ∗ , 或者一个给定策略 π π 的action-value function qπ q π ，他采用Monte Carlo 来估计给定Policy （此处为rollout policy)下，每个current state的action values。根据decision-time Planning的特点，Rollout 算法立即就使用了这些action values并将其丢弃。

Rollout Algorithms的目的在于提高原有给定policy,而不是找到optimal Policy。rollout policy越好，且value estimate越精确，rollout 算法生成的policy就越好。但是value estimate的精确估计需要大量的采样，会花去大量的计算时间，因此需要平衡value estimate的精确性和规划时间。

十二、Monte Carlo Tree Search

Monte Carlo Tree Search（MCTS) 是迄今为止，最成功的decision-time Planning算法，也是一种Rollout Algorithm，但是在Monte Carlo估计 value function的地方进行了改进，使得重点关注reward较高的trajectory的数据。对于环境模型足够简单（可以快速的进行多步仿真）的单智能体（single-agent)连续决策问题十分有效。
MCTS的核心思想是依次关注从current state开始的可以获得较高reward的trajectories。

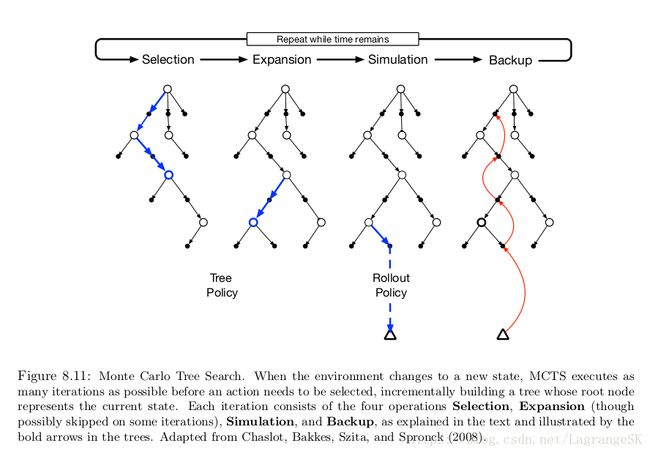
MCTS的工作过程如上图所示，每次迭代都包含四个步骤：

---

1. Selection. Starting at the root node, a tree policy based on the action values attached to the edges of the tree traverses the tree to select a leaf node.
2. Expansion. On some iterations (depending on details of the application), the tree is expanded from the selected leaf node by adding one or more child nodes reached from the selected node via unexplored actions.
3. Simulation. From the selected node, or from one of its newly-added child nodes (if any), simulation of a complete episode is run with actions selected by the rollout policy. The result is a Monte Carlo trial with actions selected first by the tree policy and beyond the tree by the rollout policy.
4. Backup. The return generated by the simulated episode is backed up to update, or to initialize,the action values attached to the edges of the tree traversed by the tree policy in this iteration of MCTS. No values are saved for the states and actions visited by the rollout policy beyond the tree. Figure 8.11 illustrates this by showing a backup from the terminal state of the simulated
   trajectory directly to the state–action node in the tree where the rollout policy began (though in general, the entire return over the simulated trajectory is backed up to this state–action node).

---

十三、总结

Planning 需要环境模型（model)。distribution model包括所有state的转移和action 带来的reward。sample model根据概率生成一系列的state 和reward。动态规划需要distribution model来计算expected update。通常sample model比distribution model容易获得。

然后我们介绍了Planning 和learning 的密切关系，都是需要通过增程式backup更新的方式估计value function，只是Planning的作用对象是model产生的simulated experience ，而learning的作用对象为 real environment 产生的real experience。并提出了Dyna结构，将Planning 、acting、model-learning结合在一起。

本章同时也介绍了state-space planning 方法的几个不同方面的变体。 第一个方面，我们关注更新的大小，更新程度越小，Planning 方法增量计算越多，最小的更新是 one-step 采样更新，如在Dyna中。另一个方面是更新的分布，是否有侧重的进行搜索，Prioritized sweeping重点关注那些values最近有变化的state-action，这可以跳过一些无关的state-action。Real-time dynamic侧重扫描那些与current state 和Policy 有关的state-action，相比完全扫描的传统DP来说提高了算法效率。

Planning 在进行决策时也需要重点关注一些states,如在采样中会出现的state。传统heuristic search是decision-time planning的一个例子，另一个例子是rollout algorithms和 Monte Carlo Tree Search。

Reinforcement Learning: an introduction