强化学习系列（六）：时间差分算法（Temporal-Difference Learning)

一、前言

在强化学习系列（五）：蒙特卡罗方法（Monte Carlo)中，我们提到了求解环境模型未知MDP的方法——Monte Carlo，但该方法是每个episode 更新一次（episode-by-episode)。本章介绍一种单步更新的求解环境模型未知MDP的方法——Temporal-Difference Learning(TD)。TD（0）算法结合了DP 和Monte Carlo算法的优点，不仅可以单步更新，而且可以根据经验进行学习。
本章同样将强化学习问题分为prediction 和 control，分别介绍TD是如何用于求解这两类问题的。

二、TD prediction

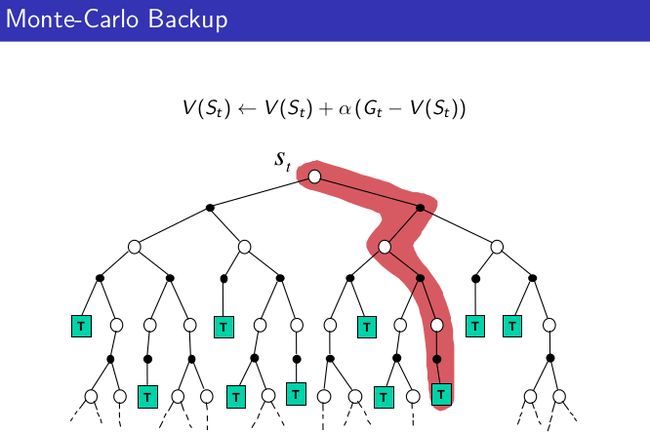
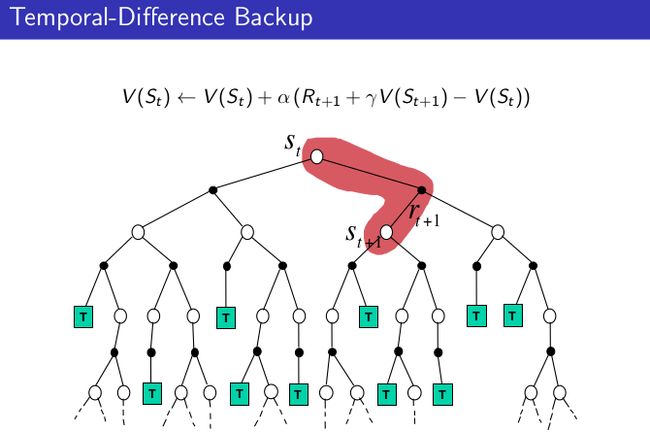
TD（0）算法结合了DP 和Monte Carlo算法的优点，不仅可以单步更新，而且可以根据经验进行学习。根据他们的backup图可以直观的看出三者区别：

MC算法需要等到一个episode 结束后才能更新value,TD和DP可以单步更新，但区别在于TD不需要知道确切的环境模型（状态转移概率等），可以根据下一步的估计来更新当前估计value。下面我们总结一下TD学习特点：

2.1 MC and TD

为了更好的理解TD算法，将其和MC算法进行进一步比较：

两者的目标都是根据经验估计给定策略 π π 下的value function v(π) v ( π )
但：

• MC更新用的是一个episode 的从state s到 terminal的实际return Gt G t ，表现为一个episode更新一次
• TD更新用的是下一个state St+1 S t + 1 的估计return Rt+1+γV(St+1） R t + 1 + γ V ( S t + 1 ） ,通常叫做TD target

这两者有什么差别呢，举个简单例子：开车回家例子， 下班回家估计到家所需时间，离开办公室估计30分钟后到家，5分钟后找到车发现下雨了，估计下雨堵车还有35分钟到家，下班20分钟时下了高速发现没有堵车，估计还有15分钟到家，结果下班30分钟时遇到堵车，估计还有10分钟到家，然后下班40分钟后到了家附近的小路上，估计还有3分钟到家，3分钟后到家了。

根据MC算法和TD算法（ γ γ )，作图如下：

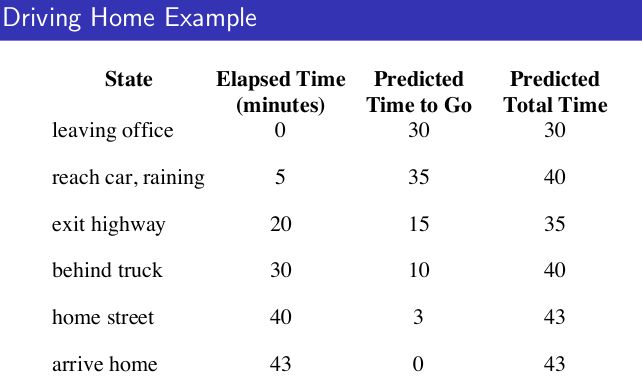
我们先看左图，运用MC算法，举个例子，当离开高速你认为还有15分钟就到家了，然而，实际需要23分钟，此时 Gt−V(St)=8 G t − V ( S t ) = 8 ,假设step size α=1/2 α = 1 / 2 ,那么预计时间会变成15+4 = 19，距离最终到家还有4分钟差值。但这些更新都是离线的，不会发生在你到家的途中，只有当到家的时候才知道原来估计的时间需要修改。
但真的需要等到回家了再调整估计时间吗？如果采用MC方法，答案是肯定的，但是采用TD就不会。可以实时对估计回家时间进行调整。

2.2 Advantages and Disadvantages of MC vs. TD

那么两者的方差和偏差如何呢？

由于TD target Rt+1+γV(St+1) R t + 1 + γ V ( S t + 1 ) 是真实的TD target Rt+1+γvπ(St+1) R t + 1 + γ v π ( S t + 1 ) 的有偏估计，所有MC是无偏差的，但TD是有偏差的。
但TD target的方差比return低，因为return依赖一系列随机的状态量和动作量，和reward ，但TD target 只依赖一组随机的状态量和动作量，和reward 。

总结一下MC和TD的算法优缺点：

2.4 TD prediction算法伪代码

三、TD control

本节针对control problem，将分别介绍on-policy TD(sarsa) 和off-policy TD (importance sample TD、QLearning、expected sarsa等)

3.1 Sarsa: On-policy TD control

和MC一样，TD中Policy evaluation 估计的是action-value function。更新方式如下：

由于更新一次action-value function需要用到5个量 (s,a,r,s′,a′) ( s , a , r , s ′ , a ′ ) ，所以该算法被称为sarsa算法，伪代码如下：

注意，第一次选择动作使用的Policy 为 ϵ ϵ -greedy policy，然后在整个episode中选择动作使用的Policy都为 ϵ ϵ -greedy policy，所以该算法为on-policy TD。

3.2 Off-policy learning

在强化学习系列（五）：蒙特卡罗方法（Monte Carlo)中，介绍了on-policy 和off- policy的区别：

• on-policy用于生成采样数据的策略和用于evlauate、improve的策略是同一个策略π 。
• off-policy用于采样的策略b （behavior policy) 和用于evlauate、improve的策略 π (target policy) 是两个不同的策略。通常情况下target policy 是确定性策略，而behavior policy是随机策略。

且在Off-policy中，提到了off-policy常用的一种方法，基于importance sample的off-policy方法。在这里我们首先介绍importance sample TD，然后介绍另一种 off-policy的思路。

3.3 Off-policy TD control：importance sample TD

在强化学习系列（五）：蒙特卡罗方法（Monte Carlo)中，我们以ordinary importance sampling 为例，比较importance sample 的MC和TD的区别。

---

importance sample MC

• 采用behavior policy b 生成的数据来估计Target policy π π
• 将b对应的return Gt G t 乘以一个importance sample ratio 可以获得Target policy π π 的return Gπ / bt G t π   /   b :（每个episode计算一次）
• Gπ / bt=π(At|St)b(At|St)π(At+1|St+1)b(At+1|St+1)...π(AT|ST)b(AT|ST)Gt G t π   /   b = π ( A t | S t ) b ( A t | S t ) π ( A t + 1 | S t + 1 ) b ( A t + 1 | S t + 1 ) . . . π ( A T | S T ) b ( A T | S T ) G t
• 然后再更新value:
• V(St)=V(St)+α(Gπ / bt−V(St)) V ( S t ) = V ( S t ) + α ( G t π   /   b − V ( S t ) )
• 当分子b为0， π π 不为零时无意义

---

可以看出， Gπ / bt G t π   /   b 与一个采样trajectory 中的所涉及的所有状态转移概率有关，因此有很高的方差，客观的说，MC算法不太适合处理off-policy问题。

对应的importance sample TD 方法：

---

importance sample TD

• 采用behavior policy b 生成的数据来估计Target policy π π
• 将b对应的TD target R+γV(S′) R + γ V ( S ′ ) 乘以一个importance sample ratio （每个step计算一次）更新value:
• V(St)=V(St)+α(π(At|St)b(At|St)(Rt+1+γV(St+1))−V(St)) V ( S t ) = V ( S t ) + α ( π ( A t | S t ) b ( A t | S t ) ( R t + 1 + γ V ( S t + 1 ) ) − V ( S t ) )

---

因为TD中的importance sample ratio 仅仅与一次概率转移比相关，所以方差比MC小，且可以单步更新。

采用importance sample的方法会导致一定的方差，在TD中还有另一种用于Off-policy TD的方法。

3.4 Off-policy TD control：Q Learning & Expected Sarsa

---

• 我们考虑不采用importance sample的另一种基于 Q(s,a) Q ( s , a ) 的off-policy learning
• 

---

当behavior Policy为 ϵ ϵ -greedy, target policy 为 greedy policy时，即可获得Q Learning 方法。

---

Q Learning

Q Learning是一种off-policy的TD方法，更新方式如下：

算法伪代码如下：

和sarsa相比，Q Learning 算法在选择动作使用的Policy 为 ϵ ϵ -greedy policy，而更新action-value function Q(s,a) Q ( s , a ) 时，用到 max Q(St+1,a) m a x   Q ( S t + 1 , a ) ，这相当于选择了greedy Policy 的action-value function，这表明生成数据使用的Policy 和评估提升使用的policy不一致，所以该算法为off-policy的TD方法。

---

Expected Sarsa

sarsa 也可以改变 Q(s,a) Q ( s , a ) 的更新形式，进而变成一种off-policy的TD方法。当更新时使用 Q(s,a) Q ( s , a ) 期望时，该算法称为Expected Sarsa：

和sarsa相比，该算法计算较为复杂，但是从由于随机选择Action所以减小了return的偏差。总体而言，当经验一样时，Expected Sarsa比sarsa表现优秀。

---

3.4 Maximization Bias and Double Learning

我们讨论的所有用于控制问题的算法都涉及到最大化target policy。例如Q learning 的target policy是greedy Policy ，而sarsa的target policy 是 ϵ ϵ -greedy policy。这些算法，最大化估计了action-value，会导致很大的正向偏差。

举个例子：考虑一个state s下所有的action对应的真实action-value q(s,a) q ( s , a ) 均为，但是估计的action-value Q(s,a) Q ( s , a ) 是不确定的，可能大于0 也可能小于0。真实的action-value的最大值为0，但估计的action-value Q(s,a) Q ( s , a ) 的最大值是正值，这导致了正向偏差。我们称之为Maximization Bias。

如何避免Maximization Bias呢？考虑第二章中提到的老虎机问题，当我们在有噪声情况下估计每个action 的value时。我们之前讨论过，如果我们采用估计action-value的最大值作为实际action-value的最大值时，会产生很大的偏差。因为我们采用同一系列的采样数据来决定最优action并估计这个action的action value。假设我们将采样数据分为两组，用他们分别产生独立的估计值 Q1(a) Q 1 ( a ) 和 Q2(a) Q 2 ( a ) ,他们的实际value都是 q(a) q ( a ) ，我们使用其中一个估计 Q1(a) Q 1 ( a ) 来决定最优action A∗=argmaxaQ1(a) A ∗ = a r g m a x a Q 1 ( a ) ,另一个估计用来估计 A∗ A ∗ 的action value Q2(A∗)=Q2(argmaxaQ1(a) Q 2 ( A ∗ ) = Q 2 ( a r g m a x a Q 1 ( a ) ,这种估计方式是无偏估计，即 E[Q2(A∗)]=q(A∗) E [ Q 2 ( A ∗ ) ] = q ( A ∗ ) 。我们可以交换两个估计的角色重复这一过程得到 Q1(argmaxaQ2(a) Q 1 ( a r g m a x a Q 2 ( a ) ，这就是double learning 的基本思想。

double learning 思想在求解MDP中运用十分广泛，我们可以结合Q Learning 得到 Double Q Learning算法，该算法中 Q1(s,a) Q 1 ( s , a ) 的更新方式如下：

算法伪代码如下：

在Double Q Learning算法中， Q1(s,a) Q 1 ( s , a ) 和 Q2(s,a) Q 2 ( s , a ) 每次以随机概率更新一个，保持另一个不变。

四、总结

本章首先TD prediction 问题，并介绍了MC 和TD的优缺点。MC是高方差无偏的episode-by-episode方法，TD是低方差有偏差的step-by-step方法。再针对TD control 问题，介绍了on-policy TD control方法sarsa，off-policy TD control 方法 Q learning、Expected Sarsa。针对这些最大化target policy的control 方法存在高偏差的问题，介绍了double learning 思想，并与Q learning 结合，介绍了double Q learning 方法。

TD方法结合了MC和DP方法的优点，使得算法可以求解无模型MDP问题，并进行单步更新，但是有些时候我们不希望进行单步更新，也不希望和MC一样等到一个episode 结束之后再更新，这就需要结合 TD 和MC方法，折中一下，就是我们下一章主要讨论的n-step Bootstrapping方法。

David Silver 课程
Reinforcement Learning: an introduction