机器学习实现原理分析(一) —— SOM简述版

代码参考：https://github.com/apachecn/AiLearning/blob/master/blog/ml/6.支持向量机.md
其他内容主要参考李航《统计学习方法》

以下是函数的输入输出，也就是算法通过迭代最后得出$b$和$\alpha$

smoSimple
        Args:
            dataMatIn    数据集
            classLabels  类别标签
            C   松弛变量(常量值)，允许有些数据点可以处于分隔面的错误一侧。
                控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
                可以通过调节该参数达到不同的结果。
            toler   容错率（是指在某个体系中能减小一些因素或选择对某个系统产生不稳定的概率。）
            maxIter 退出前最大的循环次数
        Returns:
            b       模型的常量值
            alphas  拉格朗日乘子

SOM中一个${\alpha }_i$对应一个样本点$(x_i,y_i)$,变量的总数等于训练样本容量N。

所以，一共要迭代N次：

for i in rang(shape(dataMatrix)[0])：

先随机选取一个${\alpha }_i$并带入其中求出$y_i$:已知 $y=\omega .T\ast x[i]+b$,其中 $\omega ={\Sigma }_{i=1}^n{\alpha }_i\ast y_i\ast x_i$,由此可以求出$y_i$和误差$E_i$:

  fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
  Ei = fXi - float(labelMat[i])

SMO是选择其中的两个${\alpha }_i$和${\alpha }_j$进行优化，其他值保持不变。

对于不符合KKT约束条件和发生错误的概率超过容忍值时需要进行优化，其中KKT约束条件为$0<=alphas[i]<=C$,我们用$labelMat[i]\ast E[i]$表示错误发生的概率：

if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i, m)
#随机选择非i的一点alphas[j]进行优化
# 预测j的结果
fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + b
Ej = fXj - float(labelMat[j])

假设初始可行解为${\alpha }_i^{old}$和${\alpha }_j^{old}$，最优解分别为${\alpha }_i^{new}$和${\alpha }_j^{new}$，$L$和$H$分别是${\alpha }_j^{new}$所在对角线段端点的界：
$$L<={\alpha }_j^{new}<=H$$

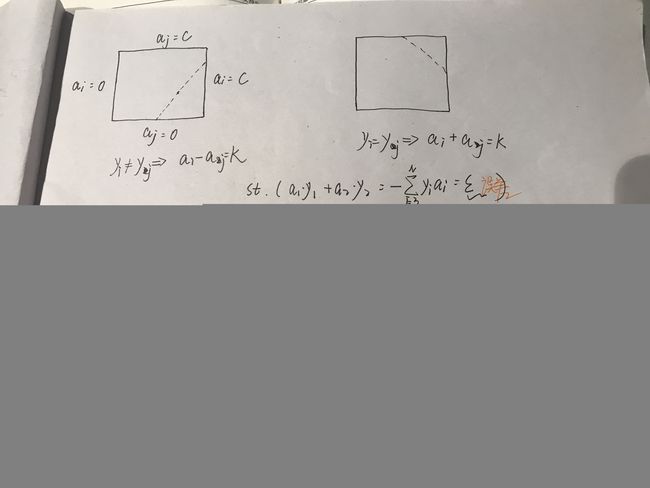
if (labelMat[i] != labelMat[j]):
    L = max(0, alphas[j] - alphas[i])
    H = min(C, C + alphas[j] - alphas[i])
else:
    L = max(0, alphas[j] + alphas[i] - C)
    H = min(C, alphas[j] + alphas[i])
# 如果相同，就没发优化了
if L == H:
    print("L==H")
    continue

先考虑沿着约束方向未考虑$0<={\alpha }_i<=C$的解(即未经剪辑)：$$g(x)={\Sigma }_{i=N}^N{a}_i\ast y_i\ast k(x_i,x)+b$$
令：$$E_i=g(x_i)-y_i$$当$i=1,2$时，$E_i$为函数对输入$x_i$的预测值和真实输出$y_i$之差

定理：最优化问题未经剪辑的解$$a_2^{new,unc}=a_2^{old}+\frac{y_2(E_1-E_2)}{\eta }$$其中，$\eta =K_{11}-2K_{12}+K_{22}=||\Phi (x_1)-\Phi (x_2)|{|}^2$

eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].T
if eta >= 0:
print("eta>=0")
continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta

然后对$a_j^{new,unc}$进行剪辑：
$$a_j^{new}=H,a_j^{new,unc}>H$$
$$a_j^{new}=a_j^{new,unc},L<=a_j^{new,unc}<=H$$
$$a_j^{new}=L,a_j^{new,unc}<L$$
最后可由$a_j^{new}$求得$a_i^{new}$:$$a_i^{new}=a_1^{old}+y_i\ast y_j(a_j^{old}-a_j^{new})$$

alphas[j] = clipAlpha(alphas[j], H, L)
def clipAlpha(aj, H, L):
    """clipAlpha(调整aj的值，使aj处于 L<=aj<=H)
    Args:
        aj  目标值
        H   最大值
        L   最小值
    Returns:
        aj  目标值
    """
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
    
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])

在每次完成两个变量的优化后，都要重新计算阈值$b$，当$0<a_1^{new}<C$时，由KKT条件可知：$${\Sigma }_i^N{a}_i\ast y_i\ast K_{i1}+b=y1$$于是，$$b_1^{new}=y_1-{\Sigma }_{i=3}^N{a}_i\ast y_i\ast K_{i1}-a_1^{new}\ast y_1\ast k_{11}-a_2^{new}\ast y_2\ast K_{21}$$由$E_i$的定义有$$E_1={\Sigma }_{i=3}^N\ast a_i\ast yi\ast k_{i1}+a_1^{old}\ast y1\ast K_{11}+a_2^{old}\ast y_2\ast K_{21}+b^{old}-y1$$整理可得：$$b_1^{new}=-E_1-(a_2^{new}-a_2^{old})\ast y_1\ast K_{12}-(a_2^{new}-a_2^{old})\ast y_2\ast k_{21}+b_{old}$$，同理，可得$b_2$

b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].T

如果$a_j^{new}$和$a_i^{new}$同时满足条件$0<a_i^{new}<C,i=1,2$,那么$b_i^{new}=b_j^{nem}$,如果他们的值是$0$或者$C$,那么$b_i^{new}$和$b_j^{new}$都是符合KKT条件的阈值，此时选择他们的中点作为$b^{new}$。

if (0 < alphas[i]) and (C > alphas[i]):
	b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
	b = b2
else:
	b = (b1 + b2)/2.0