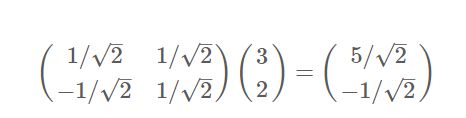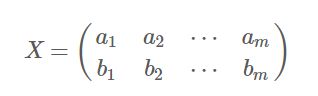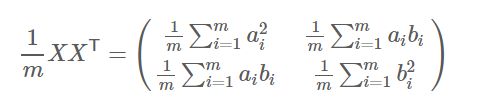数学建模学习笔记(一)--PCA
一、PCA主成分分析法
优秀文章:http://blog.codinglabs.org/articles/pca-tutorial.html
1.方差
其中N为总体数量,但是在现实中总数往往是无法得到的,所以经校正后,用n-1即样本容量-1来代替N。
2.协方差
衡量两个变量的总体误差。如果为正,说明同向变化,为负则是反向变化,大小表示程度。如果两个变量是独立的,则协方差为0(实际计算结果约等于0)。方差是协方差的特殊形式,即X,Y为同一变量,表示一个变量对其自身的数学期望的离散程度。
3.协方差矩阵
如上述公式,给定d个不同的变量,协方差矩阵就是d个变量两两求协方差,注意对角线元素本质上是求方差。明显,这是一个对称矩阵。
4.线性变换
http://mengqi92.github.io/2016/05/20/linear-algebra-3/
5.降维
用矩阵乘法[k,m]·[m,1]=[k,1]就能够将m维的向量降维到k维(k<=m),也是作基变换。如上例:向量(3,2)基变换到(1/sqrt(2),1/sqrt(2))和(-1/sqrt(2),1/sqrt(2))这两个基。
6.降维的优化目标
虽然二维降到一维时只要使结果的方差最大,就能够最大程度保存原始信息(直观上投影后尽量分散,结果向量的每个位置xi的方差最大)。但是高维的投影中,我们希望不同位置之间没有相关性,所以用方差描述是不够的。而使用协方差能够表示两个不同位置之间的相关性。
所以优化目标为:将一组N维向量降为K维,其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,不同位置上两两间协方差为0,而同一个位置上的方差则尽可能大。
7.优化的过程
首先,上面X为初始数据(这里每一行的期望为0),我们发现了下面这个事实:
上面矩阵对角线上的是不同位置的方差,非对角线上的对应位置的协方差。所以上述方法能够用来计算一个矩阵的协方差矩阵。
那么,根据上面的优化目标,就是让降维结果矩阵的协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列。
到这里,基本思想已经完成,为了简化过程,我们推导发现了下面事实:
PX=Y,P为变换基,X为原数据,Y为降维后的数据,C是X的协方差矩阵,D是Y的协方差矩阵。上面说明降维结果的协方差矩阵可以用变换基与原数据的协方差矩阵计算出来。接下来就是寻找合适的变换基P,满足计算出的D是一个对角矩阵,并且对角元素按从大到小依次排列,那么P的前K行就是要寻找的基,用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件,实际上就是矩阵D的对角化计算。
8.应用
PCA的目的就是为了简化数据的操作与运算。如降维之后,同时能够将数据解除相关性,即分类,那么我们就可以对结果做相关性的分析。
决定系数,也称为拟合优度,是相关系数的平方。表示可根据自变量的变异来解释因变量的变异部分。如某学生在某智力量表上所得的 IQ 分与其学业成绩的相关系数 r=0.66,则决定系数 R^2=0.4356,即该生学业成绩约有 44%可由该智力量表所测的智力部分来说明或决定。
同理,如果我们现在有n个变量能够描述y,我们想从n个中找出最能表达y的x,我们就可以先做PCA,判断相关性,得到决定系数最大的就是所求。在多变量选择场景中能够选择出决定性大的变量,还能够分配权重。