Treap模版

为了准备省选，终于学了平衡树（Treap），晚上的资源很多，这里只对Treap做一些简单介绍

顾名思义Treap=tree+heap，具体来说就是节点的value值是一棵二叉查找树，fix值是一个小根堆。由于fix是随机分配的，可以看作Treap是随机平衡的。经过严格的数学证明，可以证明时间复杂度为O(lgn),这里不再给出。

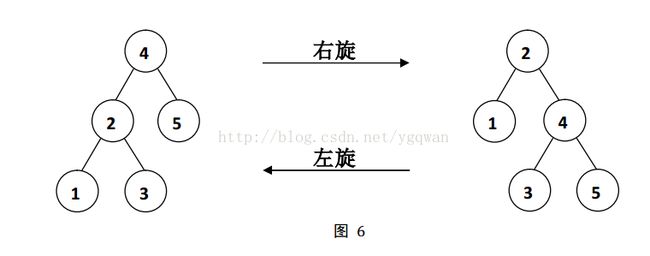
每在BST中加入一个节点，就随机分配一个fix值，如果此时不满足最小堆性质，就通过左旋（或右旋）来调整为最小堆。给出一张图（转）

删除节点时则通过左旋、右旋至某一只有一个儿子节点或叶节点上，删除即可。

求前驱，后继，排名等方法同BST，不再赘述。 模版如下：

（操作1，插入值为num的节点；操作2，删除值为num的节点；操作3，查询num的排名；操作4，查询排名为num的数；操作5，求num的前驱；操作6，求num的后继；操作7，求最小值；操作8，求最大值；merge操作此处无用,为合并两棵treap;）

#include
#include
#include
#include
#include
using namespace std;
struct treap_node{
	treap_node *left,*right;
	int val,fix,size,wgt;
	treap_node(int val): val(val)  {left=right=NULL; size=wgt=1; fix=rand();}
	int lsize()
	  {
	    if (left)
	      return left->size;
	    else 
	      return 0;
	  }
	int rsize()
	  {
	    if (right)
	      return right->size;
	    else 
	      return 0;
	  }
	void Maintain()
	  {
	    size=wgt;
	    size+=lsize()+rsize();
	  }
};
int n;
treap_node *root;
void tlr(treap_node *&a)
{
	treap_node *b=a->right;
	a->right=b->left;
	b->left=a;
	a->Maintain();
	b->Maintain();
	a=b;
}
void trr(treap_node *&a)
{
	treap_node *b=a->left;
	a->left=b->right;
	b->right=a;
	a->Maintain();
	b->Maintain();
	a=b;
}
void insert(treap_node *&p,int value)
{
	if (!p)
	  p=new treap_node(value);
	else
	  {
	    if (value==p->val)
	      p->wgt++;
	    if (valueval)
	      {
	        insert(p->left,value);
	        if (p->left->fixfix)
	          trr(p);
	      }
	    if (value>p->val)
	      {
	        insert(p->right,value);
	        if (p->right->fixfix)
	          tlr(p);
	      }
	  }
	p->Maintain();
}
void del(treap_node *&p,int value)
{
	if (value==p->val)
	  {
	    if (p->wgt==1)
	      {
	        if (!p->left||!p->right)
	          {
	            if (!p->left)
	              p=p->right;
	            else
	              p=p->left;
	          }
	        else
	          {
	            if (p->left->fixright->fix)
	              {
	                trr(p);
	                del(p->right,value);
	              }
	            else
	              {
	                tlr(p);
	                del(p->left,value);
	              }
	          }
	      }
	    else
	      p->wgt--;
	  }
	else
	  {
	    if (valueval)
	      del(p->left,value);
	    else
	      del(p->right,value);
	  }
	if (p!=NULL) p->Maintain();
}
treap_node* tpred(treap_node *&p,int value,treap_node* best)
{
	if (!p) return best;
	if (p->valright,value,p);
	else
	  return tpred(p->left,value,best);
} 
treap_node* tsucc(treap_node *&p,int value,treap_node* best)
{
	if (!p) return best;
	if (p->val>value)
	  return tsucc(p->left,value,p);
    else
	  return tsucc(p->right,value,best); 
}
treap_node* kth(treap_node *&p,int k)
{
	if (klsize()+1)
	  return kth(p->left,k);
	else
	  if (k>p->lsize()+p->wgt)
	    return kth(p->right,k-p->lsize()-p->wgt);
	  else
	    return p;
}
int rank(treap_node *&p,int value,int cur)
{
	if (value==p->val)
	  return cur+p->lsize()+1;
	else
	  if (valueval)
	    return rank(p->left,value,cur);
      else
        return rank(p->right,value,cur+p->lsize()+p->wgt);
}
void merge(treap_node *&a,treap_node *&b)
{
	if (a->left) merge(a->left,b);
	if (a->right) merge(a->right,b);
	insert(b,a->val);
}
int main()
{
	int i,kind,num,k;
	treap_node *null=NULL;
	srand(time(0)); k=0;
	scanf("%d",&n);
	for (i=1;i<=n;++i)
	  {
	  	scanf("%d",&kind);
	  	if (kind==1)
	  	  {
	  	  	k++;
	  	    scanf("%d",&num);
	  	    insert(root,num);
	      }
	  	if (kind==2)
	  	  {
	  	  	k--;
	        scanf("%d",&num);
	  	    del(root,num);
	      }
	  	if (kind==3)
	  	  {
	  	    scanf("%d",&num);
	  	    printf("%d\n",rank(root,num,0));
	      }
	  	if (kind==4)
		  {
		  	scanf("%d",&num);
		    treap_node *t;
		    t=kth(root,num);
		    printf("%d\n",t->val);
		  }  
		if (kind==5)
		  {
		  	scanf("%d",&num);
		    treap_node *t;
		    t=tpred(root,num,null);
		    printf("%d\n",t->val);
		  }
		if (kind==6)
		  {
		  	scanf("%d",&num);
		    treap_node *t;
		    t=tsucc(root,num,null);
		    printf("%d\n",t->val);
		  }
		if (kind==7)
		  {
	        treap_node *t;
			t=kth(root,1); 
		    printf("%d\n",t->val);
	      }
		if (kind==8)
		  {
		    treap_node *t;
		    t=kth(root,k);
		    printf("%d\n",t->val);
		  }
	  }
}