机器学习面试系列三
41.线性分类器与非线性分类器的区别以及优劣
如果模型是参数的线性函数,并且存在线性分类面,那么就是线性分类器,否则不是。
常见的线性分类器有:LR,贝叶斯分类,单层感知机、线性回归
常见的非线性分类器:决策树、RF、GBDT、多层感知机
SVM两种都有(看线性核还是高斯核)
线性分类器速度快、编程方便,但是可能拟合效果不会很好
非线性分类器编程复杂,但是效果拟合能力强
42.数据的逻辑存储结构(如数组,队列,树等)对于软件开发具有十分重要的影响,试对你所了解的各种存储结构从运行速度、存储效率和适用场合等方面进行简要地分析。
| |
运行速度 | 存储效率 | 适用场合 |
| 数组 | 快 | 高 | 比较适合进行查找操作,还有像类似于矩阵等的操作 |
| 链表 | 较快 | 较高 | 比较适合增删改频繁操作,动态的分配内存 |
| 队列 | 较快 | 较高 | 比较适合进行任务类等的调度 |
| 栈 | 一般 | 较高 | 比较适合递归类程序的改写 |
| 二叉树(树) | 较快 | 一般 | 一切具有层次关系的问题都可用树来描述 |
| 图 | 一般 | 一般 | 除了像最小生成树、最短路径、拓扑排序等经典用途。还被用于像神经网络等人工智能领域等等。 |
43.什么是分布式数据库?
分布式数据库系统是在集中式数据库系统成熟技术的基础上发展起来的,但不是简单地把集中式数据库分散地实现,它具有自己的性质和特征。集中式数据库系统的许多概念和技术,如数据独立性、数据共享和减少冗余度、并发控制、完整性、安全性和恢复等在分布式数据库系统中都有了不同的、更加丰富的内容。
44.简单说说贝叶斯定理。
在引出贝叶斯定理之前,先学习几个定义:
-
条件概率(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
比如,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率,所以:P(A|B) = |A∩B|/|B|,接着分子、分母都除以|Ω|得到![]()
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为![]() 或者
或者![]() 。
。
边缘概率(又称先验概率)是某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。
1.首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
2.其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
3.类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;
4.同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
上述公式的推导其实非常简单,就是从条件概率推出。
同样地,在事件A发生的条件下事件B发生的概率
整理与合并上述两个方程式,便可以得到:![]()
接着,上式两边同除以P(B),若P(B)是非零的,我们便可以得到贝叶斯定理的公式表达式:
所以,贝叶斯公式可以直接根据条件概率的定义直接推出。即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B),所以P(A|B) = P(A)P(B|A) / P(B)。更多请参见此文http://blog.csdn.net/v_july_v/article/details/40984699
45.#include和#include“filename.h”有什么区别?
用 #include 格式来引用标准库的头文件(编译器将从标准库目录开始搜索)。
用 #include “filename.h” 格式来引用非标准库的头文件(编译器将从用户的工作目录开始搜索)。
46.某超市研究销售纪录数据后发现,买啤酒的人很大概率也会购买尿布,这种属于数据挖掘的哪类问题?(A)
A. 关联规则发现 B. 聚类 C. 分类 D. 自然语言处理
47.将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C)
A. 频繁模式挖掘 B. 分类和预测 C. 数据预处理 D. 数据流挖掘
48.下面哪种不属于数据预处理的方法? (D)
A变量代换 B离散化 C 聚集 D 估计遗漏值
49.什么是KDD? (A)
A. 数据挖掘与知识发现 B. 领域知识发现 C. 文档知识发现 D. 动态知识发现
50.当不知道数据所带标签时,可以使用哪种技术促使带同类标签的数据与带其他标签的数据相分离?(B)
A. 分类 B. 聚类 C. 关联分析 D. 隐马尔可夫链
51.建立一个模型,通过这个模型根据已知的变量值来预测其他某个变量值属于数据挖掘的哪一类任务?(C)
A. 根据内容检索 B. 建模描述 C. 预测建模 D. 寻找模式和规则
52.以下哪种方法不属于特征选择的标准方法: (D)
A嵌入 B 过滤 C 包装 D 抽样
53.请用python编写函数find_string,从文本中搜索并打印内容,要求支持通配符星号和问号。
例子:
>>>find_string('hello\nworld\n','wor')
['wor']
>>>find_string('hello\nworld\n','l*d')
['ld']
>>>find_string('hello\nworld\n','o.')
['or']
答案
def find_string(str,pat):
import re
return re.findall(pat,str,re.I)
54.说下红黑树的五个性质
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。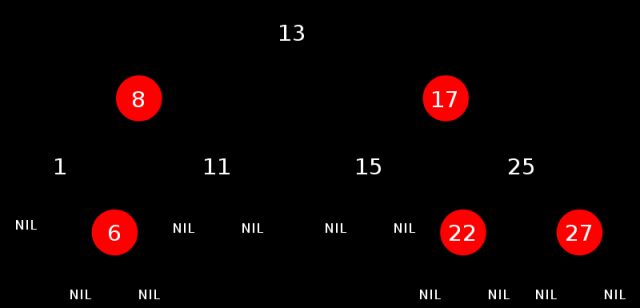
红黑树,作为一棵二叉查找树,满足二叉查找树的一般性质。下面,来了解下 二叉查找树的一般性质。
二叉查找树,也称有序二叉树(ordered binary tree),或已排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点(no duplicate nodes)。
因为一棵由n个结点随机构造的二叉查找树的高度为lgn,所以顺理成章,二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后,则这些操作最坏情况运行时间为O(n)。
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
但它是如何保证一棵n个结点的红黑树的高度始终保持在logn的呢?这就引出了红黑树的5个性质:
每个结点要么是红的要么是黑的。
根结点是黑的。
每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
如果一个结点是红的,那么它的两个儿子都是黑的。
对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。
正是红黑树的这5条性质,使一棵n个结点的红黑树始终保持了logn的高度,从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因。更多请参见此文:http://blog.csdn.net/v_july_v/article/details/6105630
55.简单说下sigmoid激活函数
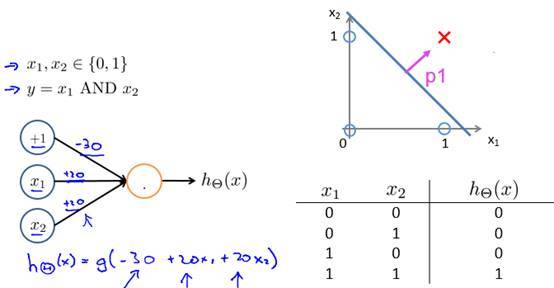
常用的非线性激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数(btw,在本博客中SVM那篇文章开头有提过)。
sigmoid的函数表达式如下
其中z是一个线性组合,比如z可以等于:b + *
+
*
。通过代入很大的正数或很小的负数到g(z)函数中可知,其结果趋近于0或1。
因此,sigmoid函数g(z)的图形表示如下( 横轴表示定义域z,纵轴表示值域g(z) ):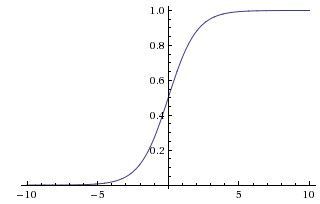
也就是说,sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时,g(z)会趋近于1,而z是非常小的负数时,则g(z)会趋近于0。
压缩至0到1有何用处呢?用处是这样一来便可以把激活函数看作一种“分类的概率”,比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。
z = b + ![]() *
*![]() +
+ ![]() *
*![]() ,其中b为偏置项 假定取-30,
,其中b为偏置项 假定取-30,![]() 、
、![]() 都取为20
都取为20
如果![]() = 0
= 0 ![]() = 0,则z = -30,g(z) = 1/( 1 + e^-z )趋近于0。此外,从上图sigmoid函数的图形上也可以看出,当z=-30的时候,g(z)的值趋近于0
= 0,则z = -30,g(z) = 1/( 1 + e^-z )趋近于0。此外,从上图sigmoid函数的图形上也可以看出,当z=-30的时候,g(z)的值趋近于0
如果![]() = 0
= 0 ![]() = 1,或
= 1,或![]() =1
=1 ![]() = 0,则z = b +
= 0,则z = b + ![]() *
*![]() +
+ ![]() *
*![]() = -30 + 20 = -10,同样,g(z)的值趋近于0
= -30 + 20 = -10,同样,g(z)的值趋近于0
如果![]() = 1
= 1 ![]() = 1,则z = b +
= 1,则z = b + ![]() *
*![]() +
+ ![]() *
*![]() = -30 + 20*1 + 20*1 = 10,此时,g(z)趋近于1。
= -30 + 20*1 + 20*1 = 10,此时,g(z)趋近于1。
换言之,只有![]() 和
和![]() 都取1的时候,g(z)→1,判定为正样本;
都取1的时候,g(z)→1,判定为正样本;![]() 或
或![]() 取0的时候,g(z)→0,判定为负样本,如此达到分类的目的。
取0的时候,g(z)→0,判定为负样本,如此达到分类的目的。
56.什么是卷积
对图像(不同的数据窗口数据)和滤波矩阵(一组固定的权重:因为每个神经元的多个权重固定,所以又可以看做一个恒定的滤波器filter)做内积(逐个元素相乘再求和)的操作就是所谓的『卷积』操作,也是卷积神经网络的名字来源。
非严格意义上来讲,下图中红框框起来的部分便可以理解为一个滤波器,即带着一组固定权重的神经元。多个滤波器叠加便成了卷积层。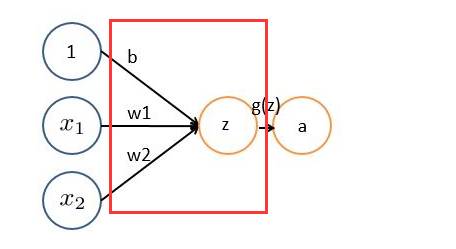
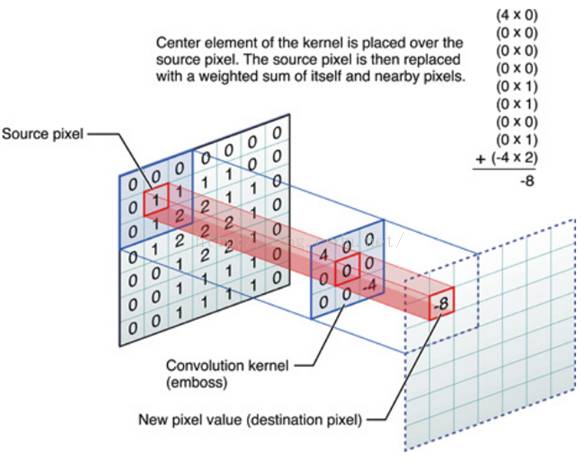
OK,举个具体的例子。比如下图中,图中左边部分是原始输入数据,图中中间部分是滤波器filter,图中右边是输出的新的二维数据。
分解下上图
中间滤波器filter与数据窗口做内积,其具体计算过程则是:4*0 + 0*0 + 0*0 + 0*0 + 0*1 + 0*1 + 0*0 + 0*1 + -4*2 = -8
57.什么是CNN的池化pool层
池化,简言之,即取区域平均或最大,如下图所示(图引自cs231n)
上图所展示的是取区域最大,即上图左边部分中 左上角2x2的矩阵中6最大,右上角2x2的矩阵中8最大,左下角2x2的矩阵中3最大,右下角2x2的矩阵中4最大,所以得到上图右边部分的结果:6 8 3 4。很简单不是?
58.简述下什么是生成对抗网络
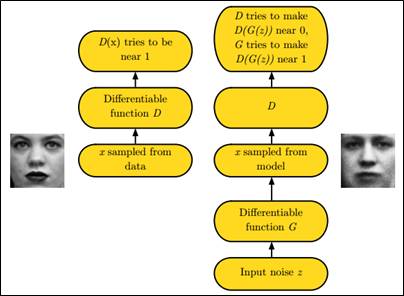
GAN之所以是对抗的,是因为GAN的内部是竞争关系,一方叫generator,它的主要工作是生成图片,并且尽量使得其看上去是来自于训练样本的。另一方是discriminator,其目标是判断输入图片是否属于真实训练样本。
更直白的讲,将generator想象成假币制造商,而discriminator是警察。generator目的是尽可能把假币造的跟真的一样,从而能够骗过discriminator,即生成样本并使它看上去好像来自于真实训练样本一样。
如下图中的左右两个场景:
更多请参见此课程:https://www.julyedu.com/course/getDetail/83
59.学梵高作画的原理是啥
这里有篇如何做梵高风格画的实验教程《教你从头到尾利用DL学梵高作画:GTX 1070 cuda 8.0 tensorflow gpu版》,至于其原理请看这个视频:NeuralStyle艺术化图片(学梵高作画背后的原理)。
60.现在有 a 到 z 26 个元素, 编写程序打印 a 到 z 中任取 3 个元素的组合(比如 打印 a b c ,d y z等)
解析参考:http://blog.csdn.net/lvonve/article/details/53320680
![]()