【Unity ShaderLab】屏幕后处理：模糊

内容

1. 简介  
2. 径向模糊
3. 均值模糊
4. 高斯模糊

---

1. 简介

    模糊是一种常见的图像处理手段，也是一种常见的后处理效果，用于降低图片细节层次。对于清晰的图像来说，像素点保存的颜色信息足够准确，图片也就能表现更多的细节。相反，要达到模糊的效果，自然就是将精准的颜色信息“舍弃”掉。

径向模糊

均值模糊

高斯模糊
 

鬼刀今天更新了吗

---

2. 径向模糊 

    径向模糊效果：从某一中心点向外呈幅射状的逐渐模糊的效果 。
    径向模糊原理：先选取屏幕坐标的一点作为中心点，选取其它每个像素点与中心点连线之间的几个点作为采样点，计算这几个采样点颜色的求和平均值，就是该像素点的值。因此，有以下几个关键点需要考虑：

• 中心点的选取：一般是屏幕坐标中心点(0.5,0.5)，如果实现GodRay的话，需要获取光源的屏幕坐标(世界坐标转屏幕坐标)作为中心点。
• 采样点的选取：常用的方式是给定采样点数量，然后计算当前像素点与中心点的距离，除以采样点数量得到步长，来确定采样点位置。
• 采样值的权重：通常为1，即采样点颜色求和再除以采样点个数。

代码如下：

Shader "Custom/PostProcess/RadialBlur" {
    Properties {
        _MainTex ("Base (RGB)", 2D) = "white" {}
    }
    CGINCLUDE
    uniform sampler2D _MainTex;
    uniform int _BlurSample;        //模糊采样个数
    uniform fixed _BlurBias;        //模糊采样偏移
    uniform fixed _BlurFactor;      //模糊步长系数
    uniform float2 _BlurCenter;     //模糊中心点(屏幕空间坐标点)

    #include "UnityCG.cginc"

    fixed4 frag(v2f_img i) : SV_Target{ 
        float2 bias = (_BlurCenter - i.uv.xy) * _BlurBias;  //模糊偏移值：由中心点到像素点的方向的偏移矢量
        float2 step = (i.uv - _BlurCenter) / _BlurSample * _BlurFactor; //计算模糊步长：决定了采样点的位置
        float2 uv = i.uv + bias;
        float4 outColor = 0;    
        for (int j = 0; j < _BlurSample; j++){                  
            uv += step;                         
            outColor += tex2D(_MainTex, uv);
        }   
        outColor /= _BlurSample;                    
        return outColor; 
    }
    ENDCG

    SubShader{
        Pass{
            ZTest Always
            Cull Off
            ZWrite Off
            Fog{ Mode off } 
            CGPROGRAM   
            #pragma fragmentoption ARB_precision_hint_fastest   
            #pragma vertex vert_img                             
            #pragma fragment frag 
            ENDCG
        }
    }
    Fallback off
}

---

3. 均值模糊 

均值模糊的原理：计算每个像素点和它周围某几个采样点的加权平均值为该像素点的值。

• 采样点的选取：一般选取当前像素点的上、下、左、右、左上、左下、右上、右下的八个像素点。
• 采样值的权重：通常为1，即采样点颜色求和再除以采样点个数。

代码如下：

Shader "Custom/PostProcess/SimpleBlur" {
	Properties{
		_MainTex("Base (RGB)", 2D) = "white" {}
	}
	CGINCLUDE
	#include "UnityCG.cginc"
	sampler2D _MainTex;
	uniform	float _BlurRadius;

	struct a2v{
		float4 vertex:POSITION;
		float2 texcoord:TEXCOORD;
	};
	struct v2f{
		float4 pos:SV_POSITION;
		half2 uv:TEXCOORD0;
		half4 uv1:TEXCOORD1;
		half4 uv2:TEXCOORD2;
		half4 uv3:TEXCOORD3;
		half4 uv4:TEXCOORD4;
	};

	v2f vert(a2v v){
		v2f o;
		o.pos = UnityObjectToClipPos(v.vertex);
		o.uv = v.texcoord;
		o.uv1.xy = v.texcoord + half2(1, 1)  *_BlurRadius;
		o.uv2.xy = v.texcoord + half2(-1, 1) *_BlurRadius;
		o.uv3.xy = v.texcoord + half2(1, -1) *_BlurRadius;
		o.uv4.xy = v.texcoord + half2(-1, -1) *_BlurRadius;
		o.uv1.zw = v.texcoord + half2(1, 0) *_BlurRadius;
		o.uv2.zw = v.texcoord + half2(-1, 0) *_BlurRadius;
		o.uv3.zw = v.texcoord + half2(0, -1) *_BlurRadius;
		o.uv4.zw = v.texcoord + half2(0, 1) *_BlurRadius;
		return o;
	}

	fixed4 frag(v2f i) :SV_Target{
		fixed4 color = tex2D(_MainTex,i.uv);
		color += color;
		color += tex2D(_MainTex,i.uv1.xy);
		color += tex2D(_MainTex,i.uv1.zw);
		color += tex2D(_MainTex,i.uv2.xy);
		color += tex2D(_MainTex,i.uv2.zw);
		color += tex2D(_MainTex,i.uv3.xy);
		color += tex2D(_MainTex,i.uv3.zw);
		color += tex2D(_MainTex,i.uv4.xy);
		color += tex2D(_MainTex,i.uv4.zw);		
		return color * 0.1;
	}
	ENDCG

	SubShader {
		Pass{
			ZTest Always
			Cull Off
			ZWrite Off
			Fog{ Mode off }
			CGPROGRAM
				#pragma vertex vert
				#pragma fragment frag
			ENDCG
		}
	}
	Fallback off
}

---

4. 高斯模糊 

4.1 正态分布

在均值模糊中，是将每一个像素和其周围的像素求和取均值从而进行模糊。但是，由于均值模糊的采样次数较少，每个像素及其周围像素的权值是相同的，模糊效果不佳，会有明显的“重影感”。这时候不得不提起另一种方法——高斯模糊。

高斯模糊(Gaussian Blur)与均值模糊中对周围像素求和取平均值不同，高斯模糊进行的是一个加权平均操作，每个像素的颜色值都是由其本身和相邻像素的颜色值进行加权平均得到的，越靠近像素本身，权值越高，越偏离像素的，权值越低。而这种权值符合我们比较熟悉的一种数学分布——正态分布，又叫高斯分布，所以这种模糊就是高斯模糊啦。

那么为了求得每个采样点的权重值，下面就要弄清楚正态分布的概念。

正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究，故正态分布又叫高斯分布。这里我们用到的是高斯分布的概率密度函数，是高斯函数的一种，以下统一简称高斯函数。

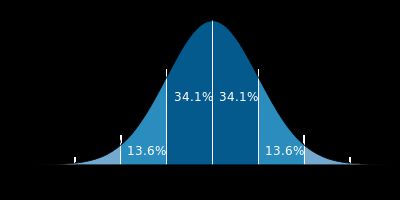
一维的高斯函数如下，其中μ为均值，σ为标准差，图像关于x=μ直线轴对称：

  标准一维 正态分布图像N(0,1)

• μ：正态分布随机变量的均值，即期望值，也就是下图中x轴上最中间的位置，随机变量在μ两侧对称分布；

• σ：为标准差，而σ^2就是这个随机变量的方差，符合正态分布的随机变量越靠近μ则概率越大，而越远离μ概率越小，σ越小，分布越集中在μ附近，σ越大，分布越分散；

• 当μ=0，σ^2=1时，称为标准正态分布，记为N(0,1)。上图就是标准正态分布的图像；

• 在 的范围内，正态分布曲线下的面积约等于整条曲线下面积的93.3%；在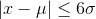的范围内，正态分布曲线下的面积约等于整条曲线下面积的99.99966%。这就意味着，在不同精度的应用场景下，3σ以外或者6σ以外的部分通常被认为是可以忽略的部分。

在因为图像分析方面，通常只考虑μ为零的情况(对于高斯模糊来说，权重最大的采样点就是当前像素点，与自身距离为0)，即：

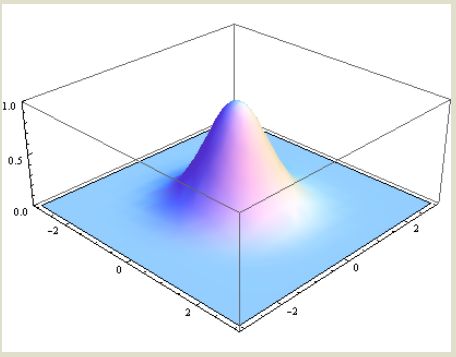
但是，我们真正需要的是二维的高斯函数，二维高斯函数实际上是由两个一维高斯函数相乘而得(μ=0)：

二维高斯函数的图像如下，其性质与一维类似，不同的是二维高斯分布具有旋转对称性，其旋转轴垂直与x,y轴所在平面：

那么为什么要使用正态分布函数作为模糊的参考依据呢？正态分布的图像呈现四周低，中间高，轴对称或者旋转对称的钟形曲线。并且许多大量统计相关的独立随机变量样本，如心理学测试分数和物理现象，其平局值的分布趋近于正态分布，尽管这些现象的根本原因经常是未知的。简而言之，正态分布函数的性质十分漂亮，可以近似模拟很多的实际现象，同样也可以作为模糊的采样参考。

---

4.2 实现思想

从实现角度来说，高斯模糊分为以下步骤：

1. 确定采样点个数，即当前像素点与哪几个周围像素做加权平均；

2. 求取每个采样点的权重值，求取的方法是利用高斯函数做采样；

3. 像素点与采样点做加权平均，即卷积。

具体操作如下：

• 确定采样点

       采样点个数和采样权重是影响模糊效果的两个重要因素。采样个数越多，那么原有像素点的”信息“比重就越少，图像也就越模糊。假定我们用n来描述原像素在x和y方向分别采样的最大个数，即卷积核的形状和大小为n×n的正方形(非必需)。

• 求采样权重

       可以通过将每个像素点的x,y坐标点位置带入高斯函数(这里的x,y是采样点相对于原像素点的偏移值)，求得权重值，但是首先我们要知道σ的值(μ=0)。
       因为已知有n×n个采样点，以x方向上离原像素点最远的那个采样点为例，其，其中k是相邻像素点之间的距离。之前说的正态分布有一条性质，在的范围内，正态分布曲线下的面积约等于整条曲线下面积的93.3%，当μ=0时，为。那么可以反过来想，我们需要正是一个为的高斯函数，这个高斯函数使得最远的采样点到原像素点之间的所有像素点分配到的权重值之和约等于93.3%，不会存在远处的采样点权重过小，或者近处的采样点权重过大的情况。
       最后，将每个像素点的x,y值坐标代入的高斯函数，得到采样权重。

• 加权平均

       终于到最后一步啦，将所有的带权采样值(采样点信息乘以该点权重值)，在除以权重值之和，就得到了当前像素点高斯模糊后的数据。(因为高斯函数图像本身是连续的，而我们的采样方式是离散的，所以不建议直接使用93.3%做为权重和)。

---

4.3 Shader实现

Shader "Custom/PostProcess/GaussianBlur" {
        Properties {
                _MainTex ("Albedo (RGB)", 2D) = "white" {}
                _BlurRadius ("_BlurRadius",Range(1,25) ) = 10
        }
        CGINCLUDE
        #include "UnityCG.cginc"

        sampler2D _MainTex;
        half4 _MainTex_TexelSize;
        int _BlurRadius;

        struct v2f{
                float4 pos : SV_POSITION; 
                float2 uv : TEXCOORD0;
        };

	float GetGaussianDistribution( float x, float y, float rho ){
	        //计算权重
	        float g = 1.0f / sqrt( 2.0f * 3.141592654f * rho * rho );
	        return g * exp( -(x * x + y * y) / (2 * rho * rho) );
	}
	float4 GetGaussBlurColor( float2 uv ){
	        //参考正态分布曲线图，可以知道 3σ 距离以外的点，权重已经微不足道了
	        //反推即可知道当模糊半径为r时，取σ为 r/3 是一个比较合适的取值
	        //即真实的模糊半径像素为R/3，映射到0~1为 R*（1/size）/3
	        float rho = (float)_BlurRadius * _MainTex_TexelSize.y / 3.0;
	        //---权重总和
	        float weightTotal = 0;
	        for( int x = -_BlurRadius ; x <= _BlurRadius ; x++ ){
	                for( int y = -_BlurRadius ; y <= _BlurRadius ; y++ ){
                            weightTotal += GetGaussianDistribution(x*_MainTex_TexelSize.y, y *_MainTex_TexelSize.y, rho );
	                }
	        }
	        float4 colorTmp = float4(0,0,0,0);
	        for( int x = -_BlurRadius ; x <= _BlurRadius ; x++ ){
	                for( int y = -_BlurRadius ; y <= _BlurRadius ; y++ ){
		            float weight = GetGaussianDistribution( x * _MainTex_TexelSize.y, y * _MainTex_TexelSize.y, rho )/weightTotal;
		        float4 color = tex2D(_MainTex,uv + float2(x * _MainTex_TexelSize.y,y * _MainTex_TexelSize.y));
		        color = color * weight;
		        colorTmp += color;
	                }
	        }    
	        return colorTmp;
	}
	v2f vert( appdata_img v ) {
	        v2f o;
	        o.pos = UnityObjectToClipPos(v.vertex);
	        o.uv = v.texcoord.xy;
	        return o;
        } 
	fixed4 frag(v2f i) : SV_Target {
	        return GetGaussBlurColor(i.uv);
        }	
	ENDCG

        SubShader {
                Tags { "RenderType"="Opaque" }
		    Pass {
		        CGPROGRAM
			        #pragma vertex vert
			        #pragma fragment frag
		        ENDCG
		    }
        }
    FallBack off
}

---

4.4 代码优化

懒癌犯了，简单说下，优化可以从以下两点考虑：

1. 选取固定大小如3×3的卷积核，提前选取合适的σ，算好采样权重值，计算时直接代入即可。不过只是这样的话，最终效果不太好，还是会有”重影感“；
2. 类似于Bloom的实现思想，可以通过降低图片的分辨率(降采样)，使效率和效果都得到提升。(因为降采样本身就具有降低图片细节的作用，即模糊效果)

---

参考文章

https://www.cnblogs.com/evennl/p/3894438.html
https://blog.csdn.net/puppet_master/article/details/52783179
https://blog.csdn.net/pz789as/article/details/79050631
https://blog.csdn.net/u011047171/article/details/47977441
https://blog.csdn.net/yaningli/article/details/78051361