Python中使用Douglas-Peucker来减少HMM识别中的状态点
手势识别中,基于手运动的位置信息,识别手势运动轨迹,由于相机采集的频率问题,导致数据点太多,HMM中显状态数量太多,使用Douglas-Peucker来减少轨迹中的运动点。
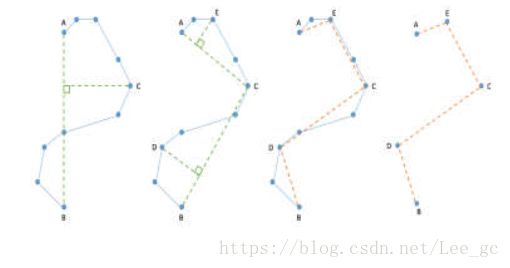
Douglas-Peucker的原理如下图所示:
自然语言表达方式如下:
1.首先以端点A,a连接作为一条直线,如果曲线Aa只包含两个端点 A a, 则此曲线去点循环结束。循环剩下所有的点,计算点与直线的垂直距离,确定与直线距离最大的点及距离ε,
2.if ε小于预定的值,那么A到a之间的所有点都被删除,使用Aa线段来代替此段曲线,此曲线段循环结束。否则曲线被分成两段Ac, ca
3.继续进行步骤1,直到满足退出循环去点条件。
最后可以看到曲线中的点的数量变少。
基于Python实现的代码粘结在下面:
import math
import re
import matplotlib.pyplot as plt
#use the dp algorithm to simplify the line.
def DPeucker(dataOrigin):
data = list()
#to make sure that the datatype is list type instead of numpy list
print(type(dataOrigin))
if(type(dataOrigin) == type([])):
print("the type is right")
else:
for i in range(dataOrigin.shape[0]):
data.append(list(dataOrigin[i]))
print(data)
removeLabel = list()
error = 0.05
label_init = lineSegments(data, 0, len(data), removeLabel, error )
#from bigger to smaller to remove the redundant data, sort it and remove the repeat data.
labelFinal = list()
label_init.sort(reverse = True)
for item in label_init:
if not item in labelFinal:
labelFinal.append(item)
#remove the redundant point
for i in range(len(labelFinal)):
del data[labelFinal[i]]
#get the point
# print(data)
return data
def calLinePara(start, end):
#input parameters is two end points
if(end[0] - start[0] != 0):#
k = (end[1] - start[1]) / (end[0] - start[0])
b = (end[0] * start[1] - end[1] * start[0]) /(end[0] - start[0])
if(end[1] - start[1] != 0):
x_axis = -b / k
else:
x_axis = None
else:
k = None
b = None#mean the paras is inexistence.
x_axis = end[0]
return (k, b, x_axis)
def dotToLIneDistance(point, k, b, a_axis):#figure out the distance from dot to line
if k == None and b == None:
distance = abs(a_axis - point[0])
else:
distance = abs(k * point[0] - point[1] + b) / math.sqrt(k * k + 1)
return distance
def lineSegments(listData, startLabel, endLabel, removeLabel, error):#recall itself to finish segments itself
# removeLabel is a list as a formal parameter, and will be changed by the function
if((endLabel - startLabel) <= 1):
return removeLabel
else:
k, b, x_axis = calLinePara(listData[startLabel], listData[endLabel-1])
distance = list()
for i in range(startLabel+1, endLabel):
# print(dotToLIneDistance(listData[i], k, b, x_axis))
distance.append(dotToLIneDistance(listData[i], k, b, x_axis))
# print(distance)
# print(max(distance))
if(max(distance) <= error):
# print(endLabel-1, startLabel)
for i in range(startLabel+1, endLabel):
# for i in range(endLabel-1,-1, int(startLabel)):
removeLabel.append(i)
else:
middleLabel = distance.index(max(distance)) + startLabel + 1
lineSegments(listData, middleLabel, endLabel, removeLabel, error)
lineSegments(listData, startLabel, middleLabel, removeLabel, error)
return removeLabelfopen = open("E:\\Research\\Unity\\RealSense\\Realsense Test\\Real Sense\\Assets\\data\\a\\Lee1.txt",'r')
lines = fopen.readlines()
dataList = list()
for line in lines:
data = re.split(' |\n',line)
# print(data)
data = [item for item in filter(lambda x: x != '', data)] # remove the blank character
# print(data)
# print(data)
# print(type(data))
for i in range(len(data)):
# print(data[i])
data[i] = float(data[i])
dataList.append(data)
x = list()
y = list()
print(dataList)
for i in range(len(dataList)):
x.append(dataList[i][0])
y.append(dataList[i][1])
fig1 = plt.figure("the origin figure")
plt.plot(x,y, 'r-*')
fig1.show()
print(len(dataList))
dataFinal = DPeucker(dataList)
# print(dataOrigin)
print(dataFinal)
print(len(dataFinal))
x_2 = list()
y_2 = list()
for i in range(len(dataFinal)):
x_2.append(dataFinal[i][0])
y_2.append(dataFinal[i][1])
fig2 = plt.figure("the processing alpha")
print(len(x_2))
plt.plot(x_2,y_2,'b-o')
fig2.show()
print("I am here")
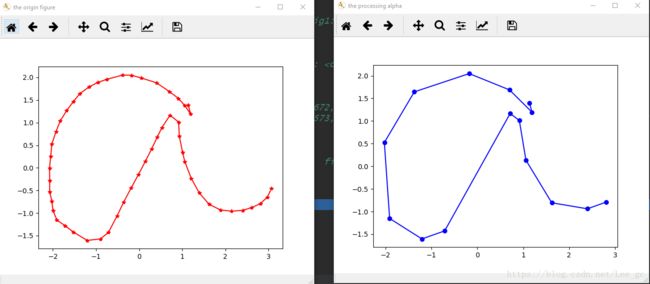
最后的实现结果如下,以手写字母a来表示,左边是原点数,右边是处理后图像