【算法设计与分析】leetcode中几道buy and sell的题目总结
这篇笔记主要记录leetcode几道buy and sell的题目解析的过程。包括:
121(Easy) Best Time to Buy and Sell Stock
122(Easy) Best Time to Buy and Sell Stock II
123(Hard) Best Time to Buy and Sell Stock III
309(Medium.) Best Time to Buy and Sell Stock with Cooldown
1.(Easy) Best Time to Buy and Sell Stock
Description:
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example 1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
这道题的意思是给你一段时间的股票价格,要求只能交易一笔,问最大可以获利多少。
做法使用两个参数来保存结果。一个res用于保存当前可以得到的最大的获利量,一个min用于保存目前最低的股票价格。代码如下:
class Solution {
public int maxProfit(int[] prices) {
if(prices==null||prices.length<2) return 0;
int res=0,min=Integer.MAX_VALUE;
for(int price : prices) {
if(price<min) min=price;
else res=Math.max(res, price-min);
}
return res;
}
}
时间复杂度O(n) ,空间复杂度O(1)
2.(Easy) Best Time to Buy and Sell Stock II
Description:
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).
Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
第一道题是单次交易的最大获利量。第二道题是可以一段时间内进行任意笔交易,但是只能同时拥有单只股票。问最大可以获利多少。
做法是,只要当前价格高于前一个价格我们就进行一笔交易。
public class Solution {
public int maxProfit(int[] prices) {
int total = 0;
for (int i=0; i< prices.length-1; i++) {
if (prices[i+1]>prices[i]) total += prices[i+1]-prices[i];
}
return total;
}
运行结果为:
时间复杂度O(n),空间复杂度为O(1)
3.(Hard)Best Time to Buy and Sell Stock III
Description:
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete at most two transactions.
Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
这道题的意思,总共只能进行两笔交易。求可以得到的最大获利量。
这道题的想法类似第一道题。第一道题使用了两个参数来保存当前最大获利和当前最小竞价,现在用4个参数buy1, sell1, buy2, sell2来扫描股票价格数组。
class Solution {
public int maxProfit(int[] prices) {
int buy1=Integer.MIN_VALUE,buy2=Integer.MIN_VALUE;
int sell1=0,sell2=0;
for(int price : prices) {
sell2=Math.max(sell2, buy2+price);
buy2=Math.max(buy2, -price+sell1);
sell1=Math.max(sell1,buy1+price);
buy1=Math.max(buy1, -price);
}
return sell2;
}
}
buy1=Math.max(buy1, -price);表示我的第一次收购价永远在找数组中的最小值
sell1=Math.max(sell1,buy1+price);sell1永远可以得到数组中的最大差价。
其实buy1和sell1扫描完整个数组的结果就是第一道题要求的结果–即只能进行一笔交易时我可以得到的最大利润。
buy2=Math.max(buy2, -price+sell1);表示我希望找到在第一次获利后可以得到的最低成本价。-price表示我买进当前股票需要付出多少钱,再加sell1表示虽然我买入股票需要花钱,但是我之前已经有通过第一笔交易得到的本金。
sell2扫描完数组后可以得到两次交易后的最大获利。
例如,对于股票价格[9,7,2,6,5,0,1,3],四个参数变化的过程如下:
| 9 | 7 | 2 | 6 | 5 | 0 | 1 | 3 | ||
|---|---|---|---|---|---|---|---|---|---|
| sell2 | 0 | 0 | 0 | 0 | 4 | 4 | 4 | 5 | 7 |
| buy2 | -∞ | -9 | -7 | -2 | -2 | -1 | 4 | 4 | 4 |
| sell1 | 0 | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 4 |
| buy1 | -∞ | -9 | -7 | -2 | -2 | -2 | 0 | 0 | 0 |
通过上面的表格可以看出:
buy1永远在找最低价格(初始值为-∞)
sell1在buy1的基础上寻找最大的获利价
buy2在sell1的基础上寻找第二次购入股票的最低价。例如当股票价为5时,虽然这个价格不是历史股票最低价(扫描到股票价为5时,当前历史股票最低价为2),但是我通过第一次获利可以得到4元(sell1=4),我在sell1的4元基础上再买入5块钱的股票时,我的总成本是-1块钱。
sell2就是最终可以得到的两笔交易后的最大累计获利。
同时这道题可以延伸到k笔交易的情形,即给定一段时间的股票价格,求出k笔交易可以带来的最大获利。
两笔交易时,我们需要4个变量,k笔交易时,我们就需要2k个变量。
将这些变量新建一个数组存起来使用即可。
4.Best Time to Buy and Sell Stock with Cooldown
Description
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]
这道题的意思是,可以进行任意笔交易,但是两笔交易之间必须冷却一天,就是第i天卖了股票之后,第i+1天不能再买入股票。
这道题和第三道题的想法类似。也是使用DP
class Solution{
public int maxProfit(int[] prices) {
int len=prices.length;
int[] buy=new int[len];
int[] sell=new int[len];
buy[0]=-prices[0];buy[1]=Math.max(-prices[0], -prices[1]);
sell[0]=0;sell[1]=Math.max(0,buy[1]+prices[1]);
for(int i=2;i<prices.length;i++) {
buy[i]=Math.max(buy[i-1], sell[i-2]-prices[i]);
sell[i]=Math.max(sell[i-1], buy[i-1]+prices[i]);
}
return sell[len-1];
}
}
buy[i]表示第i天如果我是处于股票买入状态,我能得到的最大获利是多少。
如果在第i天我是处于股票买入状态,有两种可能,一种是我前几天买入了股票,用buy[i-1]表示(不管我是昨天还是前天还是大前天买的股票,buy[i-1]都可以表示"前几天"买的股票状态);另外一种是我前天已经售出了自己的股票,今天又买了一笔新的,用sell[i-2]-prices[i]表示。
sell[i]表示第i天我是处于股票售出的状态,并且我得到的获利是sell[i]。
如果我在第i天处于股票售出状态,有两种可能,一种是我前几天已经卖出了股票,而且今天也不打算买,用sell[i-1]表示。另外一种可能是我本来手持有股票,但是今天卖出了,所以今天是处于售出状态,用(buy[i-1]+prices[i])表示。
这个代码还可以进一步优化为空间复杂度为O(1)形式:
public int maxProfit(int[] prices) {
int sell = 0, prev_sell = 0, buy = Integer.MIN_VALUE, prev_buy;
for (int price : prices) {
prev_buy = buy;
buy = Math.max(prev_sell - price, prev_buy);
prev_sell = sell;
sell = Math.max(prev_buy + price, prev_sell);
}
return sell;
}
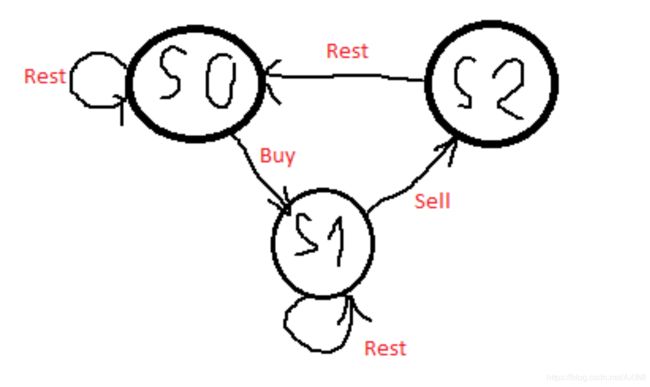
s0[i] = max(s0[i - 1], s2[i - 1]); // Stay at s0, or rest from s2
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]); // Stay at s1, or buy from s0
s2[i] = s1[i - 1] + prices[i]; // Only one way from s1
s0[0] = 0; // At the start, you don't have any stock if you just rest
s1[0] = -prices[0]; // After buy, you should have -prices[0] profit. Be positive!
s2[0] = INT_MIN; // Lower base case
class Solution {
public:
int maxProfit(vector<int>& prices){
if (prices.size() <= 1) return 0;
vector<int> s0(prices.size(), 0);
vector<int> s1(prices.size(), 0);
vector<int> s2(prices.size(), 0);
s1[0] = -prices[0];
s0[0] = 0;
s2[0] = INT_MIN;
for (int i = 1; i < prices.size(); i++) {
s0[i] = max(s0[i - 1], s2[i - 1]);
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]);
s2[i] = s1[i - 1] + prices[i];
}
return max(s0[prices.size() - 1], s2[prices.size() - 1]);
}
};