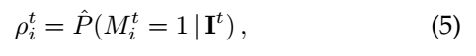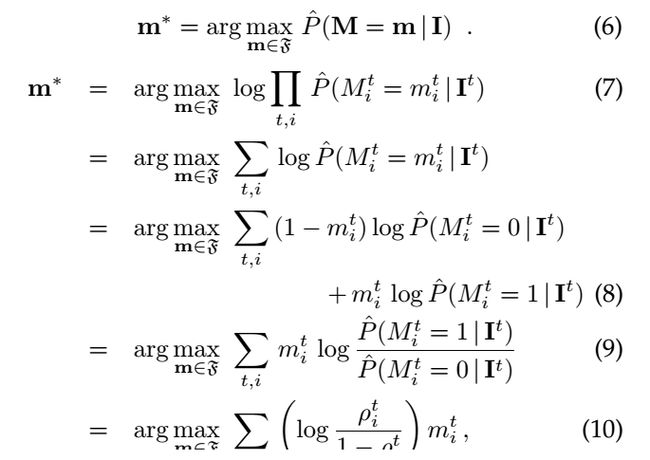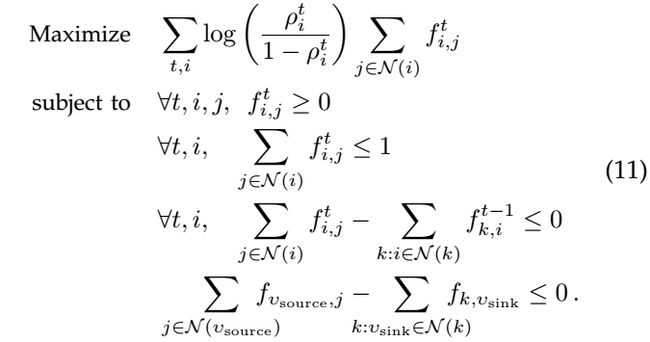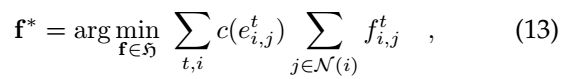论文阅读：Multiple Object Tracking Using K-Shortest Paths Optimization, PAMI2011



论文出处：Multiple ObjectTracking Using K-Shortest Paths Optimization, PAMI2011.

 

引文：

多目标跟踪问题通常分为两步：第一步是与时间无关的目标检测，即针对每一视频帧检测出目标出现的位置，以及在这些位置上出现的置信度；第二步是在时间轴上连接候选目标形成轨迹，在生成轨迹时要尽可能保证同一条轨迹上的所有目标对应同一个真实物体，轨迹数量对应目标数量。

        从数学优化的角度，已知所有候选目标求解最优轨迹的复杂度是NP完全规模的。现有的一些近似求解算法包括粒子滤波，卡尔曼滤波以及贪心动态规划等在一定程度能够获得正确轨迹（消除false positive，或更正false negtive候选），但都无法保证全局最优解。本文将轨迹求解问题转化为带约束的流优化问题，进而形成标准线性规划问题。由于约束矩阵的特殊性，恰好可以利用K最短路径算法求解该优化系统，从而获得实时性效率。与已有跟踪算法相比，本文算法具有以下优势：1）算法输入简单，只需要各候选目标的位置及置信度（Probabilistic occupancy map），由检测算法提供；2）根据优化结果（路径数量），算法能够自动输出目标数量；3）算法的控制参数较少，算法效率能够达到实时。

算法介绍：

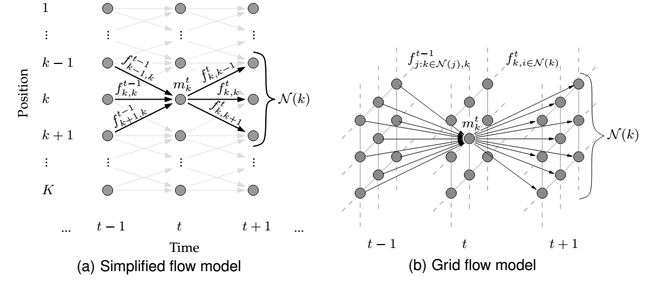
    该论文将多目标跟踪问题转化为整数规划问题。第一步是构建网络模型（Graph model）：假设当前要跟踪的视频流包含T帧，每一帧图像被检测出K个候选目标（即K个节点），相邻帧间的候选目标根据距离约束形成边连接关系。左下图为一维节点模型示意，右下图为二维节点模型示意。每个节点变量m表示当前该节点处目标物体的数量；每条边权重表示有f个目标从该条边流过。

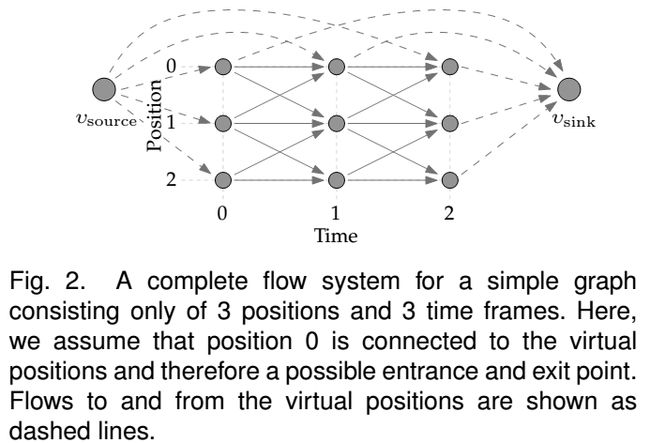
目标优化时还需要定义流的起点与终点，故增加两个虚拟节点Vsource, Vsink，一个完整的流约束图模型如下：

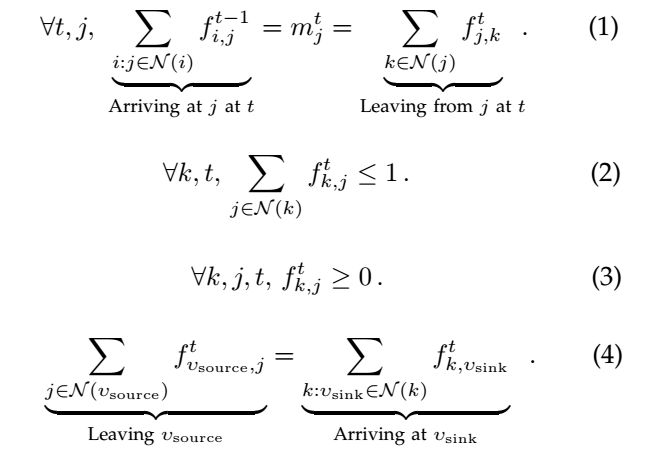
该网络模型的约束条件：

其中（1）和（4）定义了节点的流入与流出约束，即目标物体不会突然出现或消失（只能从起点Vsource出现，在终点Vsink消失），每个节点的流入与流出均衡；（2）和（3）定义了每个节点在同一时刻最多只能出现一个目标（f,m取值为0或1）。

每个节点的目标出现概率（由检测算法获得）：

该系统的优化目标是对所有节点寻找最优m集，使得全局联合概率最大：

其中（7）假设各节点条件独立，（8）是因为m取0或1,（9）是忽略掉（8）中与m无关的量，（10）为目标优化函数。至此，该整数规划的目标已相当明确，约束条件（1）~（4），m为优化待求变量（0或1），log函数已知可以认为是节点出现目标的置信度。

由m与f的关系，将上述规划稍作变换，f成为目标变量：

由于（11）的约束矩阵具备unimodularity性质，因而松弛线性规划求解方法可以收敛到整数解。但为了进一步提高求解效率，该论文使用KSP算法快速求解。

      K最短路径算法分为节点不相交的K最短路径算法和边不相交的K最短路径算法。K条节点不相交路径一定是K条边不相交路径，但反之未必。该论文使用的是节点不相交路径算法。首先将（11）中的log函数视为方向边权重：

则（11）中的目标函数转化为：

即寻找K条节点不相交最短路径，使得所有路径的Cost最小，而K就是目标数量。

        K节点不相交路径算法是一种跌代算法（http://en.wikipedia.org/wiki/Suurballe's_algorithm），Pk表示前K条路径，Pk+1的计算依赖于Pk的结果，以下是计算前两条路径的步骤：

1）使用Dijkstra算法计算从s到其他顶点的最短路径，s到各顶点u的最短距离保存为d(s,u),记s->t的最短路径为P1;

2）对P1上的除Vsource，Vsink之外的所有顶点进行split和reverse变换：节点复制，边方向反转，边权重求负；

3）边权重更新：c’(u,v)= c(u,v) + d(s,u) – d(s,v)；

4）重新计算最短路径p2*；

5）p2*与P1求并，消除掉两者中的方向相反的公共边，保留其他所有正向边，得到P2 = {p1,p2}.

论文总结：

1）该论文算法完全忽略了目标的特征关系（仅使用目标出现概率做参数优化），当两目标趋于靠近然后再分开时，优化结果极有可能导致错误的身份交换。为此，作者的另一篇论文（Tracking Multiple People under Global Appearance Constraints,ICCV2011）利用稀疏特征约束来矫正identity switch.

2）算法精度严重依赖目标出现概率（边权重系数）。

3）本文在利用KSP进行计算时，从同一顶点出发的所有边具有相同的边权重（no appearance model）,一个可行的改进：根据候选目标的相似性计算或得不同的边权重系数。

4) CSDN代码下载：http://download.csdn.net/download/lizilong_1/5833583