矩阵快速幂求Fibonacci数

Description

n the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn−1 + Fn−2 for n ≥ 2. For example, the first
ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula1 for the Fibonacci sequence is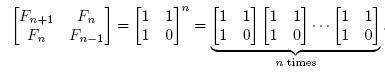

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number -1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1
Sample Output

0
34
626
6875

#include
#include
#include
#define sf(a) scanf("%d",&a)
#define pf(ans) printf("%d\n",ans)
using namespace std;
const int mod=1e4;
typedef struct node
{
    int a[10][10];
} matrix;
matrix mat_mul(matrix p,matrix q)
{
    matrix res;
    memset(res.a,0,sizeof(res.a));
    for(int i=0; i<2; i++)
        for(int j=0; j<2; j++)
            for(int k=0; k<2; k++)
            {
                res.a[i][j]+=(p.a[i][k]*q.a[k][j]);
                res.a[i][j]%=mod;
            }
    return res;
}
int fast_pow(int n)
{
    matrix mat,matr;
    mat.a[0][0]=1;
    mat.a[0][1]=1;
    mat.a[1][0]=1;
    mat.a[1][1]=0;
    memset(matr.a,0,sizeof(matr.a));
    for(int i=0; i<2; i++)
        matr.a[i][i]=1;
    while(n)
    {
        if(n%2==1)
            matr=mat_mul(matr,mat);
        mat=mat_mul(mat,mat);
        n/=2;
    }
    return matr.a[0][1];
}
int main()
{
    int n;
    while(sf(n)&&n+1)
    {
        pf(fast_pow(n));
    }
}