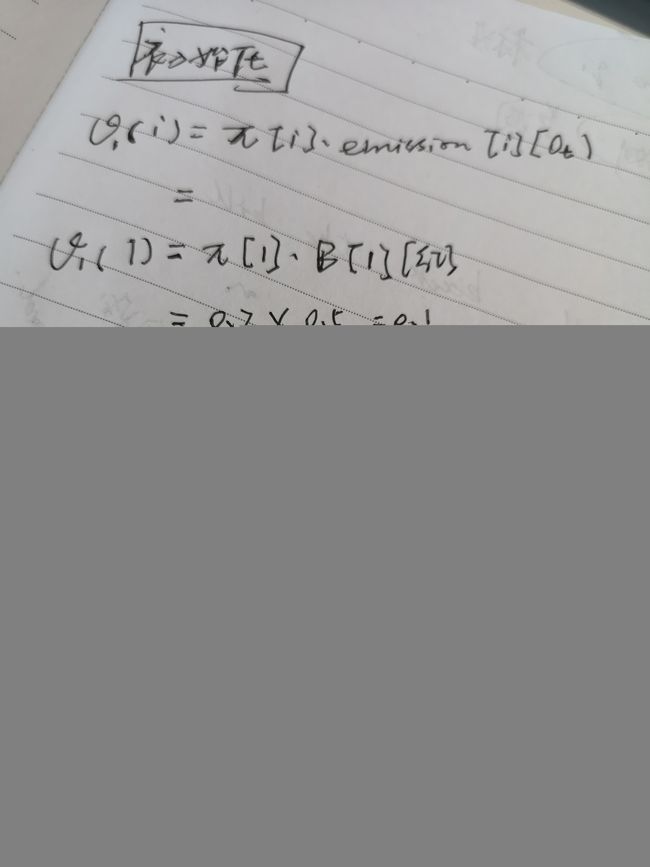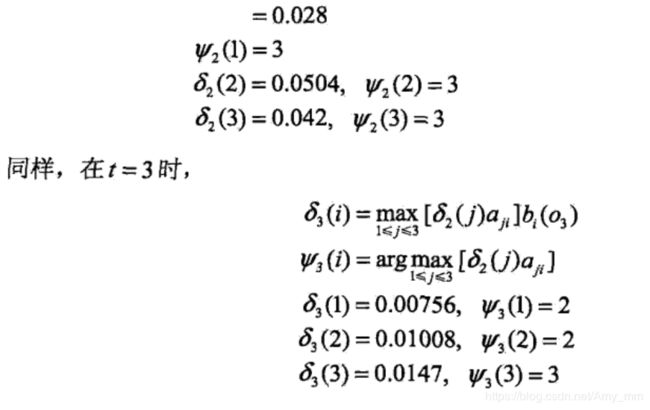HMM 实现中文词性标注 以及 维特比算法原理

【写在前边】
本人NLP小白，正在看序列标注相关问题，简单记录下学习的知识和博文，虽然大都是参考的别人的，但是字是我打的··哈哈哈
保护知识产权尊重参考博主：
参考链接：
HMM中的各种算法讲解
HMM词性标注参考原文
李航《统计学习方法》
speech and Language processing

原理：

HMM 生成式模型，利用联合概率建模，估算隐藏于观测序列背后的隐序列。
POS：单词:观测序列，词性：状态序列（隐序列）

HMM建模公式：
$$\begin{gathered} P(O)=\sum _{Q}P(O,Q) \\ =\sum _{Q}P(O|Q)P(Q) \end{gathered}$$
一阶马尔科夫假设：

1. 每个状态都是独立的，观测序列（单词）的概率只依赖于自己的tag，与相邻的单词无关。
   $P(O|Q)={\prod }_{i=1}^{n}P(o_i|q_i)$
2. 状态序列只依赖于前一个状态，也就是bigram假设。
   $P(Q)={\prod }_{i=1}^{n}P(q_i|q_{i-1})$

前半部分需要计算隐序列的各种情况也就是发射概率矩阵，后半部分需要转移概率矩阵得到。
$$P(O|Q)P(Q)=\prod _{i=1}^{n}P(o_i|q_i)\times \prod _{i=1}^{n}P(q_i|q_{i-1})$$

HMM模型
$\lambda =(A,B,\pi )$，也就是HMM中的A：转移概率矩阵，B：状态概率矩阵，$\pi$初始状态概率向量
HMM三个基本问题(图为李航老师《统计学习方法》)

1. 概率计算问题。给定HMM模型$\lambda$和观测序列O= {O1, O2…On},计算观测序列在$\lambda$下的概率$P(O|\lambda )$
2. 学习问题。已知O和模型，用极大似然的方法估计参数
3. 预测问题。也就是我们在POS中要用到的解码问题。已知模型和观测序列O，求给定观测序列下，最可能的状态序列（隐序列）。

学习问题

用极大似然概率实现学习问题，也就是得到初始概率、转移矩阵和发射矩阵。

1. $\pi$ 初始状态概率向量，在POS中定义为每个词性出现在句首的概率。
   $\pi [q]$= 词性p出现在句子开头的次数 / 句子的总数

# 定义pi为字典，pi [p] = p的初始概率
pi = defaultdict(int) 
# 学习初始概率,句子开头词性的频率
for sentence in train_data：
	pi [sentence [0] [1] ] += 1

2. 转移概率矩阵 ，POS中定义为词性P1后边紧跟着的每个词性的概率，transition [p1] [p2] 也就是词性p1后边是p2的概率
   transition [p1] [p2] = 所有句子中相邻词的二元组，词性p1后边是词性p2的个数 / 所有句子相邻词的二元组中，第一个词性是p1的总数

# 定义transition为字典。transition = { 词性p1： { 转移到的词性： 对应概率}}
transition = {}
for p in pos: # pos为所有的词性
	transition[p] = defaultdict(int)
# 学习transition
states_transition = [(p1[1],p2[1]) for p1,p2 in zip(sent,sent[1:])]
#学习转移概率
for p1,p2 in states_transition:
	transition [p1][p2] += 1

3. 发射概率矩阵 POS中是指在所有被标注为词性P的词中，词W的概率。emission [i][w]也就是词性i的情况下是w的概率，P（w | i）
   emission [p] [w] = 所有句子相邻词的二元组中，词性p的发射词w的个数 / 所有句子相邻词的二元组中，词性p的个数

#定义 同transition。emission = {词性P：{word ： 对应概率}}
emission = {}
for p in pos:
    emission [ p] = defaultdict(int)
   # 学习emission
for word，pos in sentence:
	emission [pos][word] += 1

至此，HMM三个参数的学习问题结束。
看到了关于这个概率的优化，比如进行简单的平滑或者取对数，稍后会在写一篇学习博文。虽然都是参考的大佬的，但是！大佬写出来不就是为了让小白看的吗！！dei不dei！

解码：维特比算法

在HMM和CRF中都会用到Viterbi解码，就是给定HMM模型或者CRF模型以及观测序列（词），找到最可能的状态序列（词性），也称为最优路径。

假设状态序列长度为N，观测序列长度为T，那么每个观测元素的状态都有N种可能，也就是$N^T$，时间复杂度太高。

Viterbi算法是用动态规划的思想去计算HMM或者CRF中的最优路径问题。
假设HMM 在 t时刻的状态为 i，Viterbi变量定义为前 t-1时刻是使得t时刻状态为i概率最大的路径。
也就是
$v(i)=ma{x}_{q_1,q_2...q_N}P(q_1,q_2...q_{t-1},q_t=i,o_1,o_2,...o_t\mid \lambda )$

Viterbi算法原理

输入：HMM模型$\lambda =(A,B,\pi )$, 观测序列 $O=(o_1,o_2,..o_t)$
输出：使得t时刻状态为i的最优路径$Q=(q_1,q_2..q_t)$

$v(i)=ma{x}_{q_1,q_2...q_N}P(q_1,q_2...q_{t-1},q_t=i,o_1,o_2,...o_t\mid \lambda )$

1. 初始化
   t=1时，在给定模型$\lambda$下，计算状态q1 = i 和观测序列o1同时发生的概率。
   $$\begin{array}{rl}v(i)& =P(q_1=i,o_1\mid \lambda )\\ & =P(q_1=i\mid \lambda )P(o_1\mid q_1=i,\lambda )\\ & =\pi [i]emission[i][o_t]\end{array}$$

#viterbi_matrix[t][i]表示时间t时最后一个状态为i的维特比变量
#viterbi_matrix = {t: {i: t时刻为i的概率}}
#等于前一个所有维特比变量乘以转移概率再乘以发射概率中的最大值
viterbi_matrix = defaultdict(dict)

#定义一个矩阵记录当t时刻为最后一个状态为i概率最大时，是由哪一个状态转移过来的
#backpointer_matrix[t][i]表示t时刻最后一个状态为i概率最大时的上一个状态。
#backpointer_amtrix = {t:{i: 转移到i的状态}}
backpointer_matrix = defaultdict(dict)

#初始化两个矩阵
#init Viterbi
for s in state:
	# 如果句子中首词在emission矩阵中，那么就是初始概率乘以发射矩阵
	if obs[0] in emission:
		viterbi_matrix [0][s] = pi[s] * emission[s][obs[0]]
	# 如果没有这个发射概率，就设置为0
	else:
		viterbi_matrix [0][s] = 0
	#句首记号
	backpointers_matrix[0][s] = '' 

3. 递推
   t = 2,3,…T
   将事件定义为某个状态序列和它对应得观测序列同时发生。
   那么t-1时刻的事件转移一次（j状态转移到 i 状态），发射一次（i 状态得到 t 时刻对应的观测序列），就得到了t时刻的事件。
   所以v[t][i]由t-1时刻的事件转移发射得到，而t-1时刻只有N个状态（N个词性），这N个状态的概率 也已经记录到了viterbi变量中，所以t-1时刻的viterbi变量乘以 j 转移到 i 的转移概率 再乘以 i 发射到$o_t$的发射概率，取其中最大的一个就是t时刻的viterbi变量。
   $v_t(i)=max{v}_{t-1}(j)\times transition[j][i]\times emission[i][o_t],i,j\in Q$

#计算对于t时刻i状态的维特比变量，以及记录它是由哪一个状态转移而来,states就是所有的状态
def get_max_arg(t,i):
	max_prob, argmax_pre_state = 0,0
	for j in states:
	   p = viterbi_matrix[t-1][j]*transition[j][i]*emission[i][obs[t]]
	   if p > max_prob:
	       max_prob = p
	       argmax_pre_state = j 
	return max_prob,argmax_pre_state

递推求得viterbi矩阵，每一步递推共N*N的计算量（N个状态转移到N个状态）， 共O(T N^2)

for t in range(1,T):
	for i in states: 
	    max_prob,argmax_pre_state = get_max_arg(t,i)
	    viterbi_matrix[t][i] = max_prob
	    backpointers_matrix[t][i] = argmax_pre_state

4. 终止
   查找最后时刻的最大概率和状态

max_prob_final_state, max_prob = None, 'UNK'
for j in states:
   #可能出现这个条件永不满足的情况，即最后时刻所有状态的最大可能概率都是0
   if viterbi_matrix[T-1][j] > max_prob:
       max_prob_final_state = j
       max_prob =  viterbi_matrix[T-1][j]

回溯最优路径

best_path = [max_prob_final_state ]
for t in range(T-1, 0, -1):
	try:
		#backpointers_matrix[t][best_path[-1]] 表示t时刻最后一个状态最佳状态时（best_path[-1]）概率最大时，是由哪一个状态转移而来。
		previous_state = backpointers_matrix[t][best_path[-1]]
		best_path.append(previous_state)
	except:
		best_path.append(None)

For Example:

path = viterbi(pi, transition, emisson, sentence)
#就得到了最优标注路径

Viterbi解码举例

《统计学习方法》中的例子
已知转移矩阵A，状态矩阵B，初始概率矩阵pi。观测序列为O={红，白，红}，求解最优状态序列，也就是最优路径。