这题很典型的树形dp可以看出来,但是要处理好所有的细节并不easy……至少对我来说是这样。
先dfs一遍处理出:
dp[u][0],最后一次不回来最大,
dp[u][1],不回来次大,
dp[u][2] , 回来;
(以上都是在子树范围下)(想象一下,dp[u][i]是包含了其所有子树信息的)
id[u] ,最后一次不回来的孩子id
无疑:这里最关键的,也难点部分就在于 怎么处理“次大”,有时候我们我们要求“次大”不能和“最大”同样大,或者不能在同一个子树上。但是这里的“次大”却不一样,应该说要根据在第二遍dfs里怎么用这个“次大”来决定它是怎样的。
对于每个节点它都可以网上或者往下走,比较显然最后答案为:
ans(u) = max(fa不回来+son回来,fa回来+son不回来)
设 up1是fa不回来的价值,up2是fa回来的价值。
怎么维护这个两个值呢?
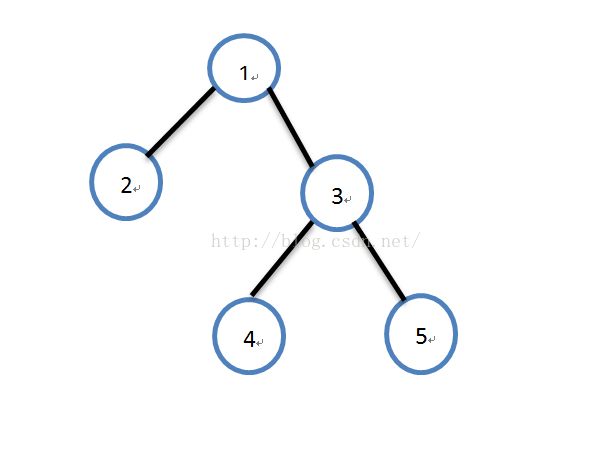
如图,令u=3,fa=1,v=5;现在我们要求v的up1和up2,
先说up1(不回来),那么对于5的父亲3来讲,它可以先去1再回3再去4不回来;也可以是先去4再回3再去1不回来,两种选择。
那么我们看一下各种代价是多少
1)去4不回来的代价d1,这里又要分两种情况
i)5==id[3]
d1= dp[3][1] - dp[5][2] + 2*cost (即3不回来的情况下减去去一趟5节点收获的价值)
ii)5!=id[3]
d1= dp[3][0] - dp[5][2] + 2*cost (即3不回来的情况下减去去一趟5节点收获的价值)
【插】关于次大:前面提到的次大到底应该怎样,就是与此处有关;可以看到在算d1的时候,
是减去了之前在去了一趟son节点收获的价值的,所以对于节点1这种情况,对于它的孩子3来说,
可以在节点1上收获的价值就是dp[1][2] - dp[3][2] + 2*cost ;所以这里的次大可以是和最大
同一个子树(因为在同一子树上也没关系,它会把要判断的son以下部分减掉)
2)去4回来的代价d2
d2 = dp[3][2] - dp[5][2] + 2*cost
那么5的up1的值也就能知道了:
up1 = max(d1+up2' , d2+up1') - cost (up1' ,up2' 为3的up1、up2)
up2比较好算,去1,去4都得回来
即: up2 = d2 + up2' - 2*cost
这样我们就算得了v(5)的up1,up2;
在代码能力强、逻辑思维清晰、题量大的大牛面前这就是一道普通题……弱还是太弱了
【代码】
/* ***********************************************
Author :angon
************************************************ */
#include
#include
#include
#include
#include
#include
#include
#include
#include
