差分隐私(Differential privacy)浅析
通过几天对差分隐私的左思右想,总算是摸到了点门道,顺着学习思路,就一些比较关键性概念说一下自己的看法:
一、关键性概念
1、查询
对数据集![]() 的各种映射函数被定义为查询(Query),用
的各种映射函数被定义为查询(Query),用 ![]() ={
={![]() ,
, ![]() , ......}来表示一组查询。
, ......}来表示一组查询。
2、邻近数据集(兄弟数据集)
设数据集![]() 与
与![]() ,具有相同的属性结构,两者对称差记作
,具有相同的属性结构,两者对称差记作![]()
![]()
![]() ,|
,|![]()
![]()
![]() |表示对称差的数量。若|
|表示对称差的数量。若|![]()
![]()
![]() |=1,则称
|=1,则称![]() 和
和![]() 为邻近数据集(又称兄弟数据集 )。
为邻近数据集(又称兄弟数据集 )。
For example:设集合![]() = {1,2,3,4,5,6},
= {1,2,3,4,5,6},![]() = {1,2,4,6},则
= {1,2,4,6},则![]()
![]()
![]() = {3,5},|
= {3,5},|![]()
![]()
![]() | = 2。
| = 2。
3、敏感度
(1)全局敏感度:
对于一个查询函数 ![]()
![]()
![]()
![]()
![]() ,其中
,其中![]() 为一个数据集,
为一个数据集,![]() 为
为![]() 维实数向量,是查询的返回结果。在任意一对邻近数据集
维实数向量,是查询的返回结果。在任意一对邻近数据集![]() 和
和![]() 上的全局敏感度为:
上的全局敏感度为:
![]() (
(![]() ) =
) = ![]()
![]()
![]() (
(![]() ) -
) - ![]() (
(![]() )
) ![]()
注意:a. ![]()
![]() (
(![]() ) -
) - ![]() (
(![]() )
) ![]() 是
是![]() (
(![]() )和
)和![]() (
(![]() )之间的曼哈顿距离;
)之间的曼哈顿距离;
b. 全局敏感度与数据集无关,只与查询结果有关。
(2)局部敏感度:
对于一个查询函数 ![]()
![]()
![]()
![]()
![]() ,其中
,其中![]() 为一个数据集,
为一个数据集,![]() 为
为![]() 维实数向量,是查询的返回结果。对于给定的数据集
维实数向量,是查询的返回结果。对于给定的数据集![]() 和它的任意邻近数据集
和它的任意邻近数据集![]() ,有
,有![]() 在
在![]() 上的局部敏感度为:
上的局部敏感度为:
![]() (
(![]() ) =
) = ![]()
![]()
![]() (
(![]() ) -
) - ![]() (
(![]() )
) ![]()
全局敏感度和局部敏感度的关系为:
![]() (
(![]() ) =
) = ![]() (
(![]() (
(![]() ))
))
二、差分隐私
设有随机算法![]() ,
,![]() 为
为![]() 所有可能的输出构成的集合,对于任意两个邻近数据集
所有可能的输出构成的集合,对于任意两个邻近数据集![]() 与
与![]() 以及
以及![]() 的任意子集
的任意子集![]() ,若算法
,若算法![]() 满足:
满足:
![]() [
[ ![]() (
(![]() )
) ![]()
![]() ]
] ![]()
![]()
![]()
![]() [
[ ![]() (
(![]() )
) ![]()
![]() ]
]
则称算法![]() 提供
提供![]() -差分隐私保护。
-差分隐私保护。
注意:a. ![]() 越小,隐私保密度越高;
越小,隐私保密度越高;
b. ![]() 越大,数据可用性越高(保密度越低);
越大,数据可用性越高(保密度越低);
c. ![]() = 0时,
= 0时,![]() 针对
针对![]() 与
与![]() 的输出概率完全相同。(这个没太搞懂~)
的输出概率完全相同。(这个没太搞懂~)
通常情况下,![]() 值取很小,
值取很小,![]() 接近于1,即对于只有一条记录差别的两个数据集,如果查询它们的概率非常非常的接近,那么它们满足差分隐私保护(通俗的说法,不太严谨)。
接近于1,即对于只有一条记录差别的两个数据集,如果查询它们的概率非常非常的接近,那么它们满足差分隐私保护(通俗的说法,不太严谨)。
For example:医院发布信息有10个人患AIDS,现在攻击者知道其中9个人的信息,通过和医院发布的信息进行比对就可以知道最后一个人是否患AIDS,这就是差分隐私攻击。如果查询9个人的信息和查询10个人的信息结果一致,那么攻击者就没有办法确定第10个人的信息,这就是差分隐私保护。
三、实现机制
1、拉普拉斯机制(常用于数值输出的函数)
(1)Laplace机制的敏感度:
给定一个函数集![]() ,
,![]() 和
和![]() 为邻近数据集,其敏感度定义如下:
为邻近数据集,其敏感度定义如下:
(2)期望为0,方差为2![]() 的Laplace分布,其概率密度函数为:
的Laplace分布,其概率密度函数为:
其中![]() =
= ![]() ,
,![]() 为敏感度。
为敏感度。
(3)Laplace机制![]() -差分隐私:
-差分隐私:
给定一个函数 ![]()
![]()
![]()
![]()
![]() ,若隐私保护算法
,若隐私保护算法![]() 满足
满足![]() -差分隐私,当且仅当下述表达式成立:
-差分隐私,当且仅当下述表达式成立:
具体公式推导证明可参考:
https://blog.csdn.net/sunjihoufeng/article/details/88068359
2、指数机制(常用于非数值输出的函数/添加数值噪声后无意义的函数)
(1)可用性函数:
设查询函数的输出域为![]() ,域中的每个值
,域中的每个值![]() 为一实体对象,
为一实体对象,![]() 为给定数据集。在指数机制下,函数
为给定数据集。在指数机制下,函数![]() 称为输出值
称为输出值![]() 的可用性函数。
的可用性函数。
(2)指数机制的敏感度:
给定可用性函数![]() ,
,![]() 和
和![]() 为任意一对邻近数据集,
为任意一对邻近数据集,![]() 为任意合法输出,其敏感度定义如下:
为任意合法输出,其敏感度定义如下:
(3)指数机制![]() -差分隐私:
-差分隐私:
给定数据集![]() 及可用性函数
及可用性函数![]() ,隐私保护机制
,隐私保护机制![]() 满足
满足![]() -差分隐私,当且仅当下述表达式成立:
-差分隐私,当且仅当下述表达式成立:
四、组合原理
1、串行组合原理(同一数据集、不同算法):
给定数据集![]() 以及一组关于
以及一组关于![]() 的差分隐私算法:
的差分隐私算法:![]() ,算法
,算法![]() 分别满足
分别满足![]() -差分隐私且任意两个算法的随机过程独立,则这些算法组合起来满足
-差分隐私且任意两个算法的随机过程独立,则这些算法组合起来满足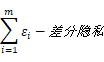 。
。
2、并行组合原理(不同数据集、不同算法):
记![]() 分别表示输入数据集为
分别表示输入数据集为![]() 的一系列满足
的一系列满足![]() -差分隐私算法且任意两个算法的随机过程相互独立,则这些算法组合起来满足
-差分隐私算法且任意两个算法的随机过程相互独立,则这些算法组合起来满足![]() -差分隐私。
-差分隐私。
3、推论(不同数据集、不同算法):
记![]() 为一系列相互独立的差分隐私,且算法
为一系列相互独立的差分隐私,且算法![]() 分别满足
分别满足![]() -差分隐私,则这些算法组合起来满足
-差分隐私,则这些算法组合起来满足![]() 。(不同数据集、不同算法,整体小于等于最大
。(不同数据集、不同算法,整体小于等于最大![]() -差分隐私)
-差分隐私)
五、心得体会
遇到一个全新的知识体系时,先不要纠结于某一个概念或者定理,要先有一个整体的知识结构,就拿差分隐私来说:
1、为了搞懂定义,我们需要一些前提知识点;
2、搞懂定义后,就去了解它的实现机制;
3、如果必要,可以再去研究它的推导证明;
4、最后,是一些延伸定理。
然后就一点一点磨,总会明白的。
That's all, good luck.