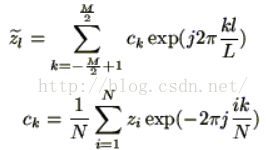图像形状特征（一）--FD

1 引言

物体的形状识别是模式识别的重要研究方向，广泛用于图像分析、机器视觉和目标识别的应用中。在计算机中物体的形状表示方式有多种：边界曲线上点的坐标序列，边界上的点到物体中心的距离以及边界上的点随弧长变化的切线方向等。基于形状不同的表示方式，已有大量的形状识别方法被提出，如：基于边界特征点，不变矩、傅里叶描绘子和自回归模型等。Kauppien 比较了各种典型的形状识别方法，实验表明基于物体轮廓坐标序列的傅里叶描述子具有最佳形状识别性能。

2 傅里叶描述子

傅里叶描述子的基本思想是：假定物体的形状是一条封闭的曲线，沿边界曲线上的一个动点P(l)的坐标变化x(l)+iy(l)是一个以形状边界周长为周期的函数，这个周期函数可以用傅里叶级数展开表示，傅里叶级数中的一系列系数z(k)是直接与边界曲线的形状有关的，称为傅里叶描述子。

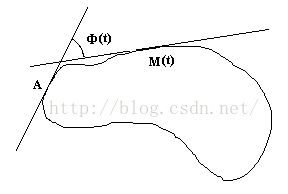
The outline of the shape is seen as a closed curve, described by its arc length s from an origin A.  We normalize this parameter so that its sum over the whole curve is equal to 2.Pi, it is the parameter t as shown below. We define a function of t, called Phi, that gives the angular variation between the tangent at the origin A and the tangent at position s.

（1）

此函数是连续的周期的（周期为2.pi）,所以可以通过傅里叶级数来表示：

（2）

式中a(k)就是傅里叶描绘子。

以下转自：http://www.tsi.telecom-paristech.fr/pages/enseignement/ressources/beti/descript_fourier/Part2.html

a. Material

We have three different parameters:

1. N: The number of points you draw (in blue)

2. M: The number of Fourier descriptors you want to use

3. L: The number of points you want to reconstruct (in red)

    This last parameter is hidden. Indeed, what you do choose on the applet (set increment) is the distance you want between the points to be reconstructed. This, compared to the length of the curve you draw, gives you L. Using the notations of the  previous section, let us explain how the reconstruction works:

        The reconstructed points are denoted  and their indice,l is restricted to the interval {0, L-1}:

with 

    If we have a careful look at the code of the applet, we can see that the set of indices chosen is not exactly the same as the one used in the theory described above. Therefore, when you set the number of Fourier descriptors to 2, you will have c(0), c(1) and c(-1) and you will not obtain a circle anymore but an ellipse.

    b. High frequencies limitation

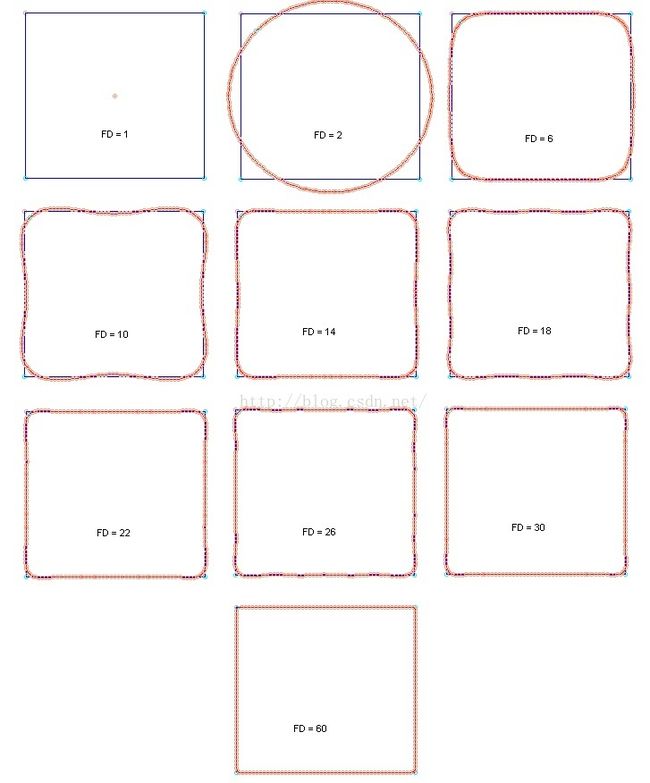
    Let us now show an experiment we performed with a square: a very simple shape. This highlights the phenomenon of forces pushing and pulling the original circle c(1)  in order to reconstruct the original square. The "high frequencies" are here materialised by the corners of the square and they are, therefore, the most demanding in high order Fourier coefficients.
.
    This confirms a very intuitive result that is : the smoother the original shape is, the easier it will be to approximate it by its lower order Fourier descriptors.

.

 

 

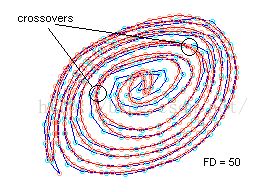
    c. Crossovers problem

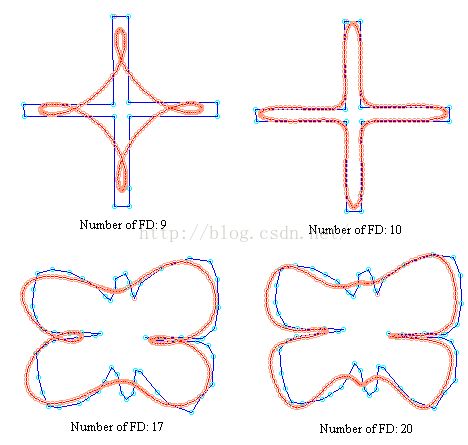
     In this subsection, we will highlight the problem of crossovers in the shape reconstructed. Indeed, as we saw at the end of theprevious section one cannot guarantee to reconstruct a shape without crossovers if the number of Fourier descriptors is not high enough.

    A very symptomatic example of this phenomenon is to try to approximate the shape of a cross: the negative indices components of the vectorC = [c(-FD/2+1) ... c(0) ... c(FD/2)]have bent the curve too much towards the inside of the circle for FD = 9 and this effect is corrected by the positive valuec(5)when FD=10. This is exactly the same for the butterfly example.

    This problem is a major drawback of this method because even with a high number of Fourier Descriptors, for some very narrow shapes, this phenomenon still occurs as we can see on the image below where the shape reconstructed uses 50 Fourier descriptors but this example can be considered as pathological.

    d. Conclusions
 

    In this subsection, we will try, starting from the caracteristics of the shape,  to know approximatly how many Fourier descriptors we must have to reconstruct it.

    Some kind of shapes are very easy to reconstruct with a small numbers of Fourier descriptors. Indeed the spectrum of these shades is mainly restricted to the low frequencies (FD<10)

        Other shapes like the square or any other figures with acute angles won't be perfectly reconstructed with these low-frequency components because of the not neglieable high frequency components they have in their spectrum.
 

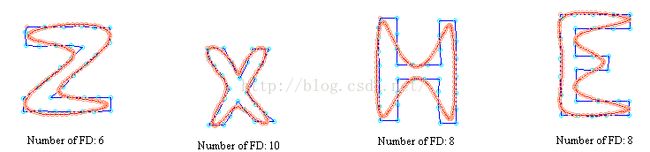
    The main advantage of this method is that the reconstructed shapes are meaningful for the eye, even with a small number of coefficients as we can figure from the example of letters below:

Therefore, the applications we can have with such a method are mainly ones performing pattern recognition. Indeed, a low-pass filtering on the shapes has the advantage of performing an average on these. Thus, comparing the first coefficients (wihoutc(0) and c(1)), will prove to be a very good object classification criterion.

原文：http://www.tsi.telecom-paristech.fr/pages/enseignement/ressources/beti/descript_fourier/index.html