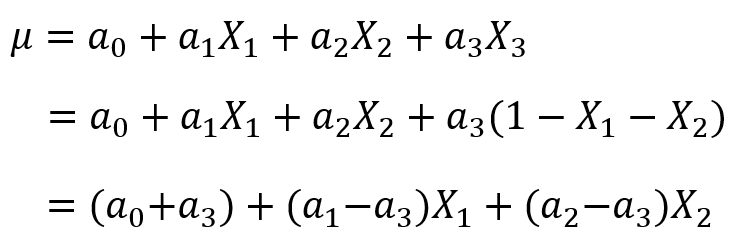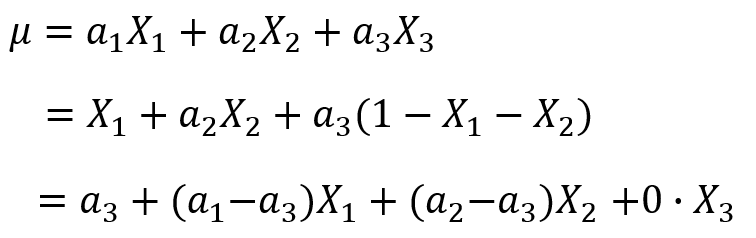系统学习机器学习之特征工程（二）--离散型特征编码方式：LabelEncoder、one-hot与哑变量*

转自：https://www.cnblogs.com/lianyingteng/p/7792693.html

在机器学习问题中，我们通过训练数据集学习得到的其实就是一组模型的参数，然后通过学习得到的参数确定模型的表示，最后用这个模型再去进行我们后续的预测分类等工作。在模型训练过程中，我们会对训练数据集进行抽象、抽取大量特征，这些特征中有离散型特征也有连续型特征。若此时你使用的模型是简单模型（如LR），那么通常我们会对连续型特征进行离散化操作，然后再对离散的特征，进行one-hot编码或哑变量编码。这样的操作通常会使得我们模型具有较强的非线性能力。那么这两种编码方式是如何进行的呢？它们之间是否有联系？又有什么样的区别？是如何提升模型的非线性能力的呢？下面我们一一介绍：

one-hot encoding

　　one-hot的基本思想：将离散型特征的每一种取值都看成一种状态，若你的这一特征中有N个不相同的取值，那么我们就可以将该特征抽象成N种不同的状态，one-hot编码保证了每一个取值只会使得一种状态处于“激活态”，也就是说这N种状态中只有一个状态位值为1，其他状态位都是0。举个例子，假设我们以学历为例，我们想要研究的类别为小学、中学、大学、硕士、博士五种类别，我们使用one-hot对其编码就会得到：

　　　　　　 

dummy encoding

　　哑变量编码直观的解释就是任意的将一个状态位去除。还是拿上面的例子来说，我们用4个状态位就足够反应上述5个类别的信息，也就是我们仅仅使用前四个状态位 [0,0,0,0] 就可以表达博士了。只是因为对于一个我们研究的样本，他已不是小学生、也不是中学生、也不是大学生、又不是研究生，那么我们就可以默认他是博士，是不是。（额，当然他现实生活也可能上幼儿园，但是我们统计的样本中他并不是，^-^）。所以，我们用哑变量编码可以将上述5类表示成：

　　　　　　

one-hot编码和dummy编码：区别与联系

　　通过上面的例子，我们可以看出它们的“思想路线”是相同的，只是哑变量编码觉得one-hot编码太罗嗦了（一些很明显的事实还说的这么清楚），所以它就很那么很明显的东西省去了。这种简化不能说到底好不好，这要看使用的场景。下面我们以一个例子来说明：

　　假设我们现在获得了一个模型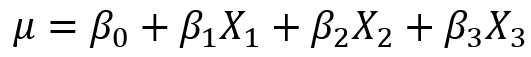，这里自变量满足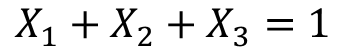（因为特征是one-hot获得的，所有只有一个状态位为1，其他都为了0，所以它们加和总是等于1），故我们可以用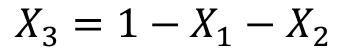表示第三个特征，将其带入模型中，得到：

　　　　　

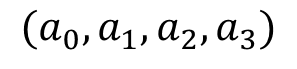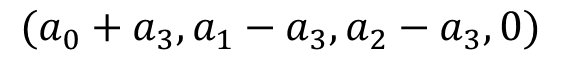这时，我们就惊奇的发现和这两个参数是等价的！那么我们模型的稳定性就成了一个待解决的问题。这个问题这么解决呢？有三种方法：

（1）使用正则化手段，将参数的选择上加一个限制，就是选择参数元素值小的那个作为最终参数，这样我们得到的参数就唯一了，模型也就稳定了。

（2）把偏置项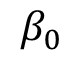去掉，这时我们发现也可以解决同一个模型参数等价的问题。

　　　　

　　因为有了bias项，所以和我们去掉bias项的模型是完全不同的模型，不存在参数等价的问题。

（3）再加上bias项的前提下，使用哑变量编码代替one-hot编码，这时去除了，也就不存在之前一种特征可以用其他特征表示的问题了。

总结：我们使用one-hot编码时，通常我们的模型不加bias项 或者 加上bias项然后使用正则化手段去约束参数；当我们使用哑变量编码时，通常我们的模型都会加bias项，因为不加bias项会导致固有属性的丢失。

选择建议：我感觉最好是选择正则化 + one-hot编码；哑变量编码也可以使用，不过最好选择前者。虽然哑变量可以去除one-hot编码的冗余信息，但是因为每个离散型特征各个取值的地位都是对等的，随意取舍未免来的太随意。

连续值的离散化为什么会提升模型的非线性能力？

 　　简单的说，使用连续变量的LR模型，模型表示为公式（1），而使用了one-hot或哑变量编码后的模型表示为公式（2）

　　　　　

式中表示连续型特征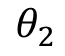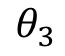，、、分别是离散化后在使用one-hot或哑变量编码后的若干个特征表示。这时我们发现使用连续值的LR模型用一个权值去管理该特征，而one-hot后有三个权值管理了这个特征，这样使得参数管理的更加精细，所以这样拓展了LR模型的非线性能力。

　　这样做除了增强了模型的非线性能力外，还有什么好处呢？这样做了我们至少不用再去对变量进行归一化，也可以加速参数的更新速度；再者使得一个很大权值管理一个特征，拆分成了许多小的权值管理这个特征多个表示，这样做降低了特征值扰动对模型为稳定性影响，也降低了异常数据对模型的影响，进而使得模型具有更好的鲁棒性。

LabelEncoder

      LabelEncoder是对不连续的数字或文本编号。

# LabelEncoder例子

  1 # -*- coding: utf-8 -*-
  2 from sklearn.preprocessing import LabelEncoder
  3 le = LabelEncoder().fit([1,111,122,188,999])
  4 le_transform = le.transform([999,122,111])
  5 print(le_transform)
  6 """
  7 [4 2 1]
  8 """