抽象代数入门（二）

Field(域)

Dfn: ”Field“ is a commutative ring , s.t. every non-zero element has inverse.

这个交换环对于乘法和加法都满足交换性，而且对于所有非零元素都存在逆。

1. 对加法逆，即
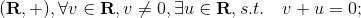
2. 对乘法逆，即

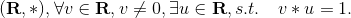
这两个都满足，u是对应元素的逆。加法的逆写成-v, 乘法的逆写成都是可以的，都是符号表示。

Polynomials over a field

Dfn: Let  be a field. A polynomial over a field  is an equation of the form :, where the coefficients . The set of all polynomials over a field  is denoted .

 

ideal(理想)

Dfn: "Idela" of  is a subset  of  s.t. it is closed under addition and closed under multiplication by any element of .

1. closed under addition: 
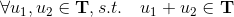
2. closed under multiplication:

i.e. the set of even integers is an ideal in the ring of integers . Given an ideal , it is possible to define a quotient ring .

i.e.  is ideal.

1. 
2. . proved

Module(模)

Dfn: a module is one of the fundamental algebraic structures used in abstract algebra. A module over a ring is a generalization of the notion of vector space over a field.

环上的一个模，域上的一个向量空间。在模中的系数是来自于环的，而向量空间中的系数是来自于域的。（域的定义更为严格，比之于环），系数的寻去空间更为通用，因此说模是向量空间的泛化。

Integral Domain(整域)

Dfn: 也叫整环，指的是不含零因子(divisor)的交换环。环中乘法的单位元通常和加法的单位元不同，整环是整数环的抽象化。关于交换环(commutative ring)的定义可以参看抽象代数入门（一）。

1. multiplicative identity element: .
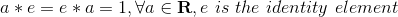2. No divisors of 0, 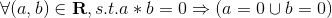 or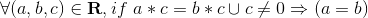 

i.e.  is an intergral domain.

Principal Ideal Ring(主理想环)

Dfn: 每个理想都可以由单个元素生成的环，写成left ideal xR or right ideal Rx 的形式，其中 x 是 环 R 中的一个元素。

Dfn: 如果交换的理想环R 同时也是整环，那么称之为主理想域(principal ideal domain), 简写成 P.I.D.

i.e. 整数环是主理想域，Eucildean Ring 一般都是。

Polynomial Ring(多项式环)

多项式环是对初等数学中多项式的泛化，通常表示成 。

Dfn: The polynomial ring,  , in  over  is defined as:

,  is the coefficient of ,  只是一个符号， 称为 powers of .

The ideal generated by a finite set of polynomials  defined as:

 

Monoic Polynomial(单多项式)

Dfn: a single-variable polynomial(univariate polynomial) in which the leading coefficient is equal to 1. Which can be written in the form:

 

Unique Factorization Domain(唯一分解环)

Dfn: 唯一分解环是一个整环(integral domain), 其元素都可以表示成有限个不可约元素乘积的形式，并在允许重排下唯一，相当于满足基本算术定理的整环。简写为UFD.

A integral domain R is said to be a unique factorization domain if it has the following factorization properties:

1. Every nonzero nonunit element 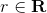 can be written as a product of a finite number of irreducible elements .
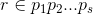2. The factorization into irreducible elements is unique in the sense that if 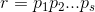 and 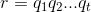 are two factorizations. Then s=t and after a suitable reindexing of the factor, . 

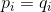Every principal ideal domain R is a unique factorization domain.