1502: [NOI2005]月下柠檬树
1502: [NOI2005]月下柠檬树
Time Limit: 5 Sec Memory Limit: 64 MBSubmit: 1077 Solved: 600
[ Submit][ Status][ Discuss]
Description
Input
文件的第1行包含一个整数n和一个实数alpha,表示柠檬树的层数和月亮的光线与地面夹角(单位为弧度)。第2行包含n+1个实数h0,h1,h2,…,hn,表示树离地的高度和每层的高度。第3行包含n个实数r1,r2,…,rn,表示柠檬树每层下底面的圆的半径。上述输入文件中的数据,同一行相邻的两个数之间用一个空格分隔。输入的所有实数的小数点后可能包含1至10位有效数字。
Output
输出1个实数,表示树影的面积。四舍五入保留两位小数。
Sample Input
2 0.7853981633
10.0 10.00 10.00
4.00 5.00
10.0 10.00 10.00
4.00 5.00
Sample Output
171.97
HINT
1≤n≤500,0.3
Source
首先要解决的大概是。。投影的形状如何?
很好想象的是,一个圆形的投影还是一个圆形,而且大小形状完全一样
而一个圆台可以当作无限个半径依次缩小的圆堆叠而成,
所以圆台的投影,是无限个离得很近,半径逐渐减小的圆,只取上下底面的投影圆作关键圆标出,大致如下![1502: [NOI2005]月下柠檬树_第2张图片](http://img.e-com-net.com/image/info8/f84147dfd8744d49b73d4e3b8faa25b9.png)
一个圆台的投影大概是两个圆以及公切线夹在它们中间的那一段
所以整个图形的投影是一段连续的图像,可以抽象成一些圆和一些公切线组成的图形
这就可以当作一个连续的函数了求函数图像下方的面积,可以使用微积分,那就用辛普森法则把它积出来
对于在区间[a,b]的函数图像,它的积分可以近似地下列方法替换
用一条过图像起止点及中间点的一条抛物线作曲边,则这个曲边梯形的面积即视作积分,有公式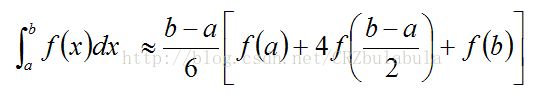
不过如果区间过长,这样的式子显然有极大误差
所以每次求完当前区间的积分后,看看左右子区间积分是否和当前区间相似
如果相似就直接返回值了,否则继续细分下去
f(x)的求法,可以暴力枚举每个圆和每条公切线,看在哪个图像上取最值
公切线的求法可以简单地用相似三角形配合三角函数做
#include
#include
#include
#include
using namespace std;
const int maxn = 505;
typedef double DB;
const DB EPS = 1E-7;
const DB INF = 1E16;
struct Point{
DB x,y; Point(){}
Point(DB x,DB y): x(x),y(y){}
Point operator * (const DB &t) {return Point(x * t,y * t);}
Point operator + (const Point &B) {return Point(x + B.x,y + B.y);}
};
typedef Point Vector;
struct Circle{
Point o; DB r;
}c[maxn];
struct Segment{
Point l,r; DB k,b; Segment(){}
Segment(Point l,Point r): l(l),r(r)
{
k = (r.y - l.y) / (r.x - l.x);
b = l.y - k * l.x;
}
}s[maxn];
int n,cnt;
DB alpha,sum;
int cmp(DB x,DB y)
{
if (fabs(x - y) <= EPS) return 0;
return x < y ? -1 : 1;
}
DB Dot(Vector v1,Vector v2) {return v1.x * v2.x + v1.y * v2.y;}
DB Length(Vector v) {return sqrt(Dot(v,v));}
DB Cal(DB c,DB a) {return sqrt(c * c - a * a);}
DB F(DB x)
{
DB ret = 0;
for (int i = 1; i < n; i++)
{
DB d = fabs(c[i].o.x - x);
if (cmp(d,c[i].r) <= 0) ret = max(ret,Cal(c[i].r,d));
}
for (int i = 1; i <= cnt; i++)
if (cmp(s[i].l.x,x) <= 0 && cmp(x,s[i].r.x) <= 0)
ret = max(ret,s[i].k * x + s[i].b);
return ret;
}
DB Calc(DB L,DB R)
{
DB A = (R - L) / 6.00;
DB B = (F(L) + 4.00 * F((L + R) / 2.00) + F(R));
return A * B;
}
DB Simpson(DB L,DB R,DB now)
{
DB mid = (L + R) / 2.00;
DB A = Calc(L,mid),B = Calc(mid,R);
if (!cmp(A + B,now)) return now;
return Simpson(L,mid,A) + Simpson(mid,R,B);
}
DB Work()
{
DB L = c[n].o.x - c[n].r,R = c[n].o.x + c[n].r;
for (int i = 1; i < n; i++)
{
L = min(L,c[i].o.x - c[i].r); R = max(R,c[i].o.x + c[i].r);
if (cmp(c[i+1].o.x - c[i+1].r,c[i].o.x - c[i].r) <= 0) continue;
if (cmp(c[i+1].o.x + c[i+1].r,c[i].o.x + c[i].r) <= 0) continue;
if (!cmp(c[i].r,c[i+1].r))
{
Point l = c[i].o + Point(0,c[i].r);
Point r = c[i+1].o + Point(0,c[i+1].r);
s[++cnt] = Segment(l,r); continue;
}
DB d = c[i+1].o.x - c[i].o.x,r1 = c[i].r,r2 = c[i+1].r;
if (r1 > r2) swap(r1,r2); DB delta = r1 * d / (r2 - r1);
DB theta = asin(r2 / (delta + d)),len; Vector v; Point p,l,r;
if (c[i].r < c[i+1].r) p = Point(c[i].o.x - delta,0),v = Point(1,tan(theta));
else p = Point(c[i+1].o.x + delta,0),v = Point(-1,tan(theta));
len = Length(v);
l = p + v * (Cal(delta,r1) / len);
r = p + v * (Cal(delta + d,r2) / len);
if (l.x > r.x) swap(l,r); s[++cnt] = Segment(l,r);
}
return Simpson(L,R,Calc(L,R));
}
int main()
{
#ifdef DMC
freopen("DMC.txt","r",stdin);
#endif
cin >> n >> alpha; ++n;
for (int i = 1; i <= n; i++)
{
DB h; scanf("%lf",&h);
sum += h; c[i].o = Point(sum / tan(alpha),0);
}
for (int i = 1; i < n; i++) scanf("%lf",&c[i].r); c[n].r = 0;
printf("%.2lf\n",Work() * 2.00);
return 0;
} ![1502: [NOI2005]月下柠檬树_第1张图片](http://img.e-com-net.com/image/info8/7be79bb0247e42ada69d74a3b2e1e572.jpg)