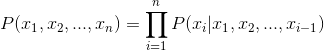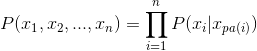- android系统selinux中添加新属性property
辉色投像
1.定位/android/system/sepolicy/private/property_contexts声明属性开头:persist.charge声明属性类型:u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
- 探索OpenAI和LangChain的适配器集成:轻松切换模型提供商
nseejrukjhad
langchaineasyui前端python
#探索OpenAI和LangChain的适配器集成:轻松切换模型提供商##引言在人工智能和自然语言处理的世界中,OpenAI的模型提供了强大的能力。然而,随着技术的发展,许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具,集成了多种模型提供商,通过提供适配器,简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成,以便轻松切换模型提供商
- 使用Apify加载Twitter消息以进行微调的完整指南
nseejrukjhad
twittereasyui前端python
#使用Apify加载Twitter消息以进行微调的完整指南##引言在自然语言处理领域,微调模型以适应特定任务是提升模型性能的常见方法。本文将介绍如何使用Apify从Twitter导出聊天信息,以便进一步进行微调。##主要内容###使用Apify导出推文首先,我们需要从Twitter导出推文。Apify可以帮助我们做到这一点。通过Apify的强大功能,我们可以批量抓取和导出数据,适用于各类应用场景。
- 深入理解 MultiQueryRetriever:提升向量数据库检索效果的强大工具
nseejrukjhad
数据库python
深入理解MultiQueryRetriever:提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域,高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用,但仍存在一些局限性。本文将介绍一种创新的解决方案:MultiQueryRetriever,它通过自动生成多个查询视角来增强检索效果,提高结果的相关性和多样性。MultiQueryRetriever的工
- pyecharts——绘制柱形图折线图
2224070247
信息可视化pythonjava数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd)数据可视化团队研发的ECharts1.0发布到GitHub网站以来,ECharts一直备受业界权威的关注并获得广泛好评,成为目前成熟且流行的数据可视化图表工具,被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言,也加入ECharts的使用行列,并研发出方便Python开发者使用的数据
- 数据仓库——维度表一致性
墨染丶eye
背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕,完整连接为:数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看,当一系列星型模型共享一组公共维度时,所涉及的维度称为一致性维度。当维度表存在不一致时,短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别,因为维度的差别,分析工作涉及的领域从简单到复杂,但是都是通过复杂的报表来弥补设计
- ARM驱动学习之基础小知识
JT灬新一
ARM嵌入式arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购(能不能买到,价格)–原理图(涉及到稳定性)•layout画板工程师–layout(封装、布局,布线,log)(涉及到稳定性)–焊接的一部分工作(调试阶段板子的焊接)•驱动工程师–驱动,原理图,layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案,原理图(网表)–layout工程师(gerber文件)–PCB板
- 展现思维导图魅力,不断挖掘人生宝藏
思维导图讲师Mandy
第13期最强思维导图训练营已经结束一周了,但是我依旧是感觉所有学员还在努力的学习,这些学员中有教师、学生、白领、公务员、宝妈等等,只要你努力,只要你想改变自己,任何行业,任何岗位都可以参与进来,28天足以让你见成效,在这28天中,我们的学员不仅仅是收获了一枚毕业证,最重要的是让自己的思维方式得到升级,今天的你为自己投资,明天的你就会感谢你今天的付出,我们来听一听来自13期最强思维导图训练营优秀学员
- 2019-11-04复盘——飞来山上千寻塔,闻说鸡鸣见日升。
那一叶秋
1、大盘篇先上老图,看习惯了,也就知道走势了图1上证指数日线图还是那张老图,自己可以在自己的相关软件上画出来,快变盘了。2、个股篇未加仓、未减仓。分析量能的时候,突然发现这么一个东西:“放量突破年线,缩量回调。”合众科技日线图其实,最近的N只个股,在技术分析上,都到了变盘的临界时候。结合这么久的走势,特别是ZJH不断放开IPO的申请,本质上说是融资难度变大,或者说是为企业的融资开创便利。但现在市场
- Java企业面试题3
马龙强_
java
1.break和continue的作用(智*图)break:用于完全退出一个循环(如for,while)或一个switch语句。当在循环体内遇到break语句时,程序会立即跳出当前循环体,继续执行循环之后的代码。continue:用于跳过当前循环体中剩余的部分,并开始下一次循环。如果是在for循环中使用continue,则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
- 父母教育孩子的方式,将影响孩子一生
树英教育
为什么有些孩子总是充满自信与快乐?独立、有主见又坚强?而有些孩子却自卑、胆怯,软弱又过度依赖父母?为什么有些孩子总是健康、阳光又富于创造力?而有些孩子却悲观、孤僻又思想空乏?一个孩子的行为取决于孩子的思想,思想取决于环境和自己的认知,认知取决于教育。父母是孩子人生中的第一位教育者,父母养育孩子的方式,将决定他们人生的高度,影响他们的一生。网络图,侵权即删优秀的父母就像园丁,既要浇水施肥,又要修剪杂
- 自然语言处理_tf-idf
_feivirus_
算法机器学习和数学自然语言处理tf-idf逆文档频率词频
importpandasaspdimportmath1.数据预处理docA="Thecatsatonmyface"docB="Thedogsatonmybed"wordsA=docA.split("")wordsB=docB.split("")wordsSet=set(wordsA).union(set(wordsB))print(wordsSet){'on','my','face','sat',
- 系统架构设计师 需求分析篇二
AmHardy
软件架构设计师系统架构需求分析面向对象分析分析模型UML和SysML
面向对象分析方法1.用例模型构建用例模型一般需要经历4个阶段:识别参与者:识别与系统交互的所有事物。合并需求获得用例:将需求分配给予其相关的参与者。细化用例描述:详细描述每个用例的功能。调整用例模型:优化用例之间的关系和结构,前三个阶段是必需的。2.用例图的三元素参与者:使用系统的用户或其他外部系统和设备。用例:系统所提供的服务。通信关联:参与者和用例之间的关系,或用例与用例之间的关系。3.识别参
- 黄景瑜工作人员怒怼营销号!肖战事件就是他的前车之鉴
板凳吃瓜小分队
无论社会怎样浮躁,我们自己也不可以浮躁。战胜浮躁的关键是明白自己真正的需要,保持一颗平常心,不要盲目攀比,不要羡慕别人,更不要唯利是图。一辈子很短,我们不能总是望着别人的精彩,羡慕着别人的人生,而忘记了经营自己生活,要知道,通过努力,你也能成为让人仰望的明星。如今,随着娱乐产业越来越成熟,每年的新星也是扎堆冒出。在我看来,与前几年不同的是,如今的新生代质量明显好过从前。“更专业了,更有礼貌了”也是
- 2023-06-19【感恩日记】第246篇
o泡沫o
思想日记:坚持下去,相信自己一定可以的【感恩日记】第246篇1.我真是太幸福啦!感恩孩子早起阅读,放学到学生之家完成作业,平安度过美好的一天。感恩!感恩!感恩!❤️2.我真是太幸福啦!感恩自己早起给孩子煮早餐,完成计划的工作,晚上学习。感恩!感恩!感恩!❤️3.我真是太幸福啦!感恩为我设计效果图的老师。感恩!感恩!感恩!❤️4.我真是太幸福啦!感恩父母养育了我,有妈的孩子真幸福。感恩!感恩!感恩!
- 摄影小白,怎么才能拍出高大上产品图片?
是波妞唉
很多人以为文案只要会码字,会排版就OK了!说实话,没接触到这一行的时候,我的想法更简单,以为只要会写字就行!可是真做了文案才发现,码字只是入门级的基本功。一篇文章离不开排版、配图,说起来很简单!从头做到尾你就会发现,写文章用两个小时,找合适的配图居然要花掉半天的时间,甚至更久!图片能找到合适的就不怕,还有找不到的,比如产品图,只能亲自拍。拿着摆弄了半天,就是拍不出想要的效果,光线不好、搭出来丑破天
- 【Bugs】Python:“ModuleNotFoundError: No module named ‘XXX‘”
系'辞
工具箱pythonbuganaconda
问题描述Python使用库的前提是必须已安装了相应的库,往往利用“命令行指令”实现安装,一般安装解法类似。但,还是具有延伸问题,本博客对此作记录。【1】Nomodulenamed‘seaborn’(1.1):情况1:为Anaconda安装【图1-2】.定位Anaconda路径【图3】.Anaconda路径加入Path>&
- 3286、穿越网格图的安全路径
Lenyiin
题解c++算法leetcode
3286、[中等]穿越网格图的安全路径1、题目描述给你一个mxn的二进制矩形grid和一个整数health表示你的健康值。你开始于矩形的左上角(0,0),你的目标是矩形的右下角(m-1,n-1)。你可以在矩形中往上下左右相邻格子移动,但前提是你的健康值始终是正数。对于格子(i,j),如果grid[i][j]=1,那么这个格子视为不安全的,会使你的健康值减少1。如果你可以到达最终的格子,请你返回tr
- 阅读《别说你懂思维导图》21~23章day27
Ling宝尔
合理期待——思维导图的应用效果很多人问我,思维导图真的有用么?我常常回答,如果你觉得是它“没用”,一定是因为你没“用”,有“用”才“有用”。实际上,学习思维导图和学习木工、驾驶等技能型学习一样,都要经历从了解到应用、从应用到受益的过程。在使用前,我们很多人的思维处于“无意识的低效”状态,经过一段时间的学习,虽然掌握了思维导图的基本使用方法,但可能并没有太好的效果,这个阶段可称为“有意识的低效”状态
- GenVisR 基因组数据可视化实战(三)
11的雾
3.genCov画每个突变位点附件的coverage,跟igv有点相似。这个操作起来很复杂,但是图还是挺有用的。可以考虑。由于我的referencegenomebuild是hg38BiocManager::install(c("TxDb.Hsapiens.UCSC.hg38.knownGene","BSgenome.Hsapiens.UCSC.hg38"))library(TxDb.Hsapien
- 小西妈双语工程打卡2018-1-18
慢蜗牛Erica
这是送给妈妈的,还有一张是爸爸的,现在看着这张小图,觉得好温暖。早上看到了我把它折上了,还好一顿不高兴。妈妈这个是爸爸。爸爸希望之星,Herewecome.复赛通知书这是送给妈妈的小鹿,栩栩如生吧,不过妈妈不确定这是他一个人完成的。还送了妈妈一个小蝴蝶发卡,很暖心哦。小鹿上完课回家就很晚了,自己看了好几本书,没有录阅读打卡。听peppa第一季3集。
- 免费的GPT可在线直接使用(一键收藏)
kkai人工智能
gpt
1、LuminAI(https://kk.zlrxjh.top)LuminAI标志着一款融合了星辰大数据模型与文脉深度模型的先进知识增强型语言处理系统,旨在自然语言处理(NLP)的技术开发领域发光发热。此系统展现了卓越的语义把握与内容生成能力,轻松驾驭多样化的自然语言处理任务。VisionAI在NLP界的应用领域广泛,能够胜任从机器翻译、文本概要撰写、情绪分析到问答等众多任务。通过对大量文本数据的
- 推荐3家毕业AI论文可五分钟一键生成!文末附免费教程!
小猪包333
写论文人工智能AI写作深度学习计算机视觉
在当前的学术研究和写作领域,AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容,还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器:千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手,旨在帮助用户快速生成高质
- AI论文题目生成器怎么用?9款论文写作网站简单3步搞定
小猪包333
写论文人工智能深度学习计算机视觉
在当今信息爆炸的时代,AI写作工具的出现极大地提高了写作效率和质量。本文将详细介绍9款优秀的论文写作网站,并重点推荐千笔-AIPassPaper。一、千笔-AIPassPaper千笔-AIPassPaper是一款功能强大的AI论文生成器,基于最新的自然语言处理技术,能够一键生成高质量的毕业论文、开题报告等文本内容。它不仅提供智能选题、文献推荐和论文润色等功能,还具有较高的用户评价。其文献综述生成功
- 这样旅行的人,值得拥有丰富而饱满的体验
究竟
01“一张车票就实现了来拉萨的梦想。原以为很遥远,现也觉得旅途值得。也不过山河故人而已。”打开朋友圈,看到了强子新发的动态,配了两张图,一张图里是拉萨火车站,另一张图里是二十来张排列得整整齐齐的火车票,终点站都是拉萨。又想起几天前,姑娘秀了一波在青海湖的美照,照片里的她,身穿鲜艳的红色长裙,坐在牦牛背上,阳光打下来,她笑靥如花。橙色的旗子风中飘扬,那蓝绿色的青海湖和天空再美,也都成了陪衬。再看看自
- AI大模型的架构演进与最新发展
季风泯灭的季节
AI大模型应用技术二人工智能架构
随着深度学习的发展,AI大模型(LargeLanguageModels,LLMs)在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进,包括从Transformer的提出到GPT、BERT、T5等模型的历史演变,并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍:Transformer的核心原理Transformer架构的背景在Transfo
- 轻风拂柳《春意萦怀》之六
轻风拂柳
图/来自网络轻风拂柳《春意萦怀》之六轻风拂柳《春意萦怀》原韵烂熳芳林赏丽容,春光明媚盼相逢。娇桃绽蕊仙姿艳,淑杏凝脂玉色浓。对对黄莺穿树影,双双彩蝶逐花踪。风情小雅灵犀有,景美难将笔墨封。图/来自网络步轻风拂柳《春意萦怀》原韵(一)诗·时就三月阳春思丽容,花红柳绿也相逢。不歆桃蕊风姿艳,只慕书斋墨色浓。期翼共窗难觅影,时望携手苦寻踪。天涯海角君何有?一颗痴心哪日封?(二)诗·大漠孤烟滴翠丛林展媚容
- 新月|图卡5-8《心》一切始于心,终于心
新月_f578
大家好,我是坚持做图卡,不断精进的新月,近期阅读书籍《心。》,持续输出图卡……截止目前已经读完本书,输出卡片9张~借助9张卡片,回顾本书的整体内容,结构上可以分为:始于心-修心-终于心。首先明确:我们为什么要这么做?其次懂得如何去做,落实到具体的方式方法上,就是修心的过程。最后是知道目标在哪,不断自我提升,向目标靠进,使修心贯穿始终。
- 读《红楼梦》第十九回 情切切良宵花解语 意绵绵静日玉生香
梦一场_c315
元春回宫,贾府上下又忙碌了二三日,方收拾停当,个个是累得人仰马翻。王熙凤为了不落人口舌也只能硬撑着,凡事冲在前头。袭人的母亲来面见贾母,将袭人接回去吃年饭,晚上才会回来,宝玉甚觉无聊。宁府这边唱戏,贾珍来邀宝玉过府观赏,刚欲出门,元春赐了糖蒸酥酪来,宝玉想着平日里袭人最爱吃,便留给袭人,自己出门看戏去了。到了宁府,只闻锣鼓喧天,热闹非凡,宝玉稍坐了片刻,忽想起一间小书房里挂着一张美人图,今日府上这
- 干货|自我介绍这三个坑,99%的概率你踩过!
夏麦生命的魔术师
自我介绍——每个人都需要的一张名片。图片源自网络从2018年到现在,在做演讲俱乐部的2年时间里,我在演讲活动现场听过1000+人的自我介绍,自我介绍做得超棒的人真不多!最近,我花了近几个月时间,仔细研究了500+人线上场景的自我介绍,发现优秀的自我介绍也不多!为什么做一张优秀的自我介绍就这么难呢?这个问题,在我帮几十个人打造了自我介绍的过程一直困扰着我。经过了几个月的时间思考与实践,终于发现三个—
- Java 并发包之线程池和原子计数
lijingyao8206
Java计数ThreadPool并发包java线程池
对于大数据量关联的业务处理逻辑,比较直接的想法就是用JDK提供的并发包去解决多线程情况下的业务数据处理。线程池可以提供很好的管理线程的方式,并且可以提高线程利用率,并发包中的原子计数在多线程的情况下可以让我们避免去写一些同步代码。
这里就先把jdk并发包中的线程池处理器ThreadPoolExecutor 以原子计数类AomicInteger 和倒数计时锁C
- java编程思想 抽象类和接口
百合不是茶
java抽象类接口
接口c++对接口和内部类只有简介的支持,但在java中有队这些类的直接支持
1 ,抽象类 : 如果一个类包含一个或多个抽象方法,该类必须限定为抽象类(否者编译器报错)
抽象方法 : 在方法中仅有声明而没有方法体
package com.wj.Interface;
- [房地产与大数据]房地产数据挖掘系统
comsci
数据挖掘
随着一个关键核心技术的突破,我们已经是独立自主的开发某些先进模块,但是要完全实现,还需要一定的时间...
所以,除了代码工作以外,我们还需要关心一下非技术领域的事件..比如说房地产
&nb
- 数组队列总结
沐刃青蛟
数组队列
数组队列是一种大小可以改变,类型没有定死的类似数组的工具。不过与数组相比,它更具有灵活性。因为它不但不用担心越界问题,而且因为泛型(类似c++中模板的东西)的存在而支持各种类型。
以下是数组队列的功能实现代码:
import List.Student;
public class
- Oracle存储过程无法编译的解决方法
IT独行者
oracle存储过程
今天同事修改Oracle存储过程又导致2个过程无法被编译,流程规范上的东西,Dave 这里不多说,看看怎么解决问题。
1. 查看无效对象
XEZF@xezf(qs-xezf-db1)> select object_name,object_type,status from all_objects where status='IN
- 重装系统之后oracle恢复
文强chu
oracle
前几天正在使用电脑,没有暂停oracle的各种服务。
突然win8.1系统奔溃,无法修复,开机时系统 提示正在搜集错误信息,然后再开机,再提示的无限循环中。
无耐我拿出系统u盘 准备重装系统,没想到竟然无法从u盘引导成功。
晚上到外面早了一家修电脑店,让人家给装了个系统,并且那哥们在我没反应过来的时候,
直接把我的c盘给格式化了 并且清理了注册表,再装系统。
然后的结果就是我的oracl
- python学习二( 一些基础语法)
小桔子
pthon基础语法
紧接着把!昨天没看继续看django 官方教程,学了下python的基本语法 与c类语言还是有些小差别:
1.ptyhon的源文件以UTF-8编码格式
2.
/ 除 结果浮点型
// 除 结果整形
% 除 取余数
* 乘
** 乘方 eg 5**2 结果是5的2次方25
_&
- svn 常用命令
aichenglong
SVN版本回退
1 svn回退版本
1)在window中选择log,根据想要回退的内容,选择revert this version或revert chanages from this version
两者的区别:
revert this version:表示回退到当前版本(该版本后的版本全部作废)
revert chanages from this versio
- 某小公司面试归来
alafqq
面试
先填单子,还要写笔试题,我以时间为急,拒绝了它。。时间宝贵。
老拿这些对付毕业生的东东来吓唬我。。
面试官很刁难,问了几个问题,记录下;
1,包的范围。。。public,private,protect. --悲剧了
2,hashcode方法和equals方法的区别。谁覆盖谁.结果,他说我说反了。
3,最恶心的一道题,抽象类继承抽象类吗?(察,一般它都是被继承的啊)
4,stru
- 动态数组的存储速度比较 集合框架
百合不是茶
集合框架
集合框架:
自定义数据结构(增删改查等)
package 数组;
/**
* 创建动态数组
* @author 百合
*
*/
public class ArrayDemo{
//定义一个数组来存放数据
String[] src = new String[0];
/**
* 增加元素加入容器
* @param s要加入容器
- 用JS实现一个JS对象,对象里有两个属性一个方法
bijian1013
js对象
<html>
<head>
</head>
<body>
用js代码实现一个js对象,对象里有两个属性,一个方法
</body>
<script>
var obj={a:'1234567',b:'bbbbbbbbbb',c:function(x){
- 探索JUnit4扩展:使用Rule
bijian1013
java单元测试JUnitRule
在上一篇文章中,讨论了使用Runner扩展JUnit4的方式,即直接修改Test Runner的实现(BlockJUnit4ClassRunner)。但这种方法显然不便于灵活地添加或删除扩展功能。下面将使用JUnit4.7才开始引入的扩展方式——Rule来实现相同的扩展功能。
1. Rule
&n
- [Gson一]非泛型POJO对象的反序列化
bit1129
POJO
当要将JSON数据串反序列化自身为非泛型的POJO时,使用Gson.fromJson(String, Class)方法。自身为非泛型的POJO的包括两种:
1. POJO对象不包含任何泛型的字段
2. POJO对象包含泛型字段,例如泛型集合或者泛型类
Data类 a.不是泛型类, b.Data中的集合List和Map都是泛型的 c.Data中不包含其它的POJO
- 【Kakfa五】Kafka Producer和Consumer基本使用
bit1129
kafka
0.Kafka服务器的配置
一个Broker,
一个Topic
Topic中只有一个Partition() 1. Producer:
package kafka.examples.producers;
import kafka.producer.KeyedMessage;
import kafka.javaapi.producer.Producer;
impor
- lsyncd实时同步搭建指南——取代rsync+inotify
ronin47
1. 几大实时同步工具比较 1.1 inotify + rsync
最近一直在寻求生产服务服务器上的同步替代方案,原先使用的是 inotify + rsync,但随着文件数量的增大到100W+,目录下的文件列表就达20M,在网络状况不佳或者限速的情况下,变更的文件可能10来个才几M,却因此要发送的文件列表就达20M,严重减低的带宽的使用效率以及同步效率;更为要紧的是,加入inotify
- java-9. 判断整数序列是不是二元查找树的后序遍历结果
bylijinnan
java
public class IsBinTreePostTraverse{
static boolean isBSTPostOrder(int[] a){
if(a==null){
return false;
}
/*1.只有一个结点时,肯定是查找树
*2.只有两个结点时,肯定是查找树。例如{5,6}对应的BST是 6 {6,5}对应的BST是
- MySQL的sum函数返回的类型
bylijinnan
javaspringsqlmysqljdbc
今天项目切换数据库时,出错
访问数据库的代码大概是这样:
String sql = "select sum(number) as sumNumberOfOneDay from tableName";
List<Map> rows = getJdbcTemplate().queryForList(sql);
for (Map row : rows
- java设计模式之单例模式
chicony
java设计模式
在阎宏博士的《JAVA与模式》一书中开头是这样描述单例模式的:
作为对象的创建模式,单例模式确保某一个类只有一个实例,而且自行实例化并向整个系统提供这个实例。这个类称为单例类。 单例模式的结构
单例模式的特点:
单例类只能有一个实例。
单例类必须自己创建自己的唯一实例。
单例类必须给所有其他对象提供这一实例。
饿汉式单例类
publ
- javascript取当月最后一天
ctrain
JavaScript
<!--javascript取当月最后一天-->
<script language=javascript>
var current = new Date();
var year = current.getYear();
var month = current.getMonth();
showMonthLastDay(year, mont
- linux tune2fs命令详解
daizj
linuxtune2fs查看系统文件块信息
一.简介:
tune2fs是调整和查看ext2/ext3文件系统的文件系统参数,Windows下面如果出现意外断电死机情况,下次开机一般都会出现系统自检。Linux系统下面也有文件系统自检,而且是可以通过tune2fs命令,自行定义自检周期及方式。
二.用法:
Usage: tune2fs [-c max_mounts_count] [-e errors_behavior] [-g grou
- 做有中国特色的程序员
dcj3sjt126com
程序员
从出版业说起 网络作品排到靠前的,都不会太难看,一般人不爱看某部作品也是因为不喜欢这个类型,而此人也不会全不喜欢这些网络作品。究其原因,是因为网络作品都是让人先白看的,看的好了才出了头。而纸质作品就不一定了,排行榜靠前的,有好作品,也有垃圾。 许多大牛都是写了博客,后来出了书。这些书也都不次,可能有人让为不好,是因为技术书不像小说,小说在读故事,技术书是在学知识或温习知识,有
- Android:TextView属性大全
dcj3sjt126com
textview
android:autoLink 设置是否当文本为URL链接/email/电话号码/map时,文本显示为可点击的链接。可选值(none/web/email/phone/map/all) android:autoText 如果设置,将自动执行输入值的拼写纠正。此处无效果,在显示输入法并输
- tomcat虚拟目录安装及其配置
eksliang
tomcat配置说明tomca部署web应用tomcat虚拟目录安装
转载请出自出处:http://eksliang.iteye.com/blog/2097184
1.-------------------------------------------tomcat 目录结构
config:存放tomcat的配置文件
temp :存放tomcat跑起来后存放临时文件用的
work : 当第一次访问应用中的jsp
- 浅谈:APP有哪些常被黑客利用的安全漏洞
gg163
APP
首先,说到APP的安全漏洞,身为程序猿的大家应该不陌生;如果抛开安卓自身开源的问题的话,其主要产生的原因就是开发过程中疏忽或者代码不严谨引起的。但这些责任也不能怪在程序猿头上,有时会因为BOSS时间催得紧等很多可观原因。由国内移动应用安全检测团队爱内测(ineice.com)的CTO给我们浅谈关于Android 系统的开源设计以及生态环境。
1. 应用反编译漏洞:APK 包非常容易被反编译成可读
- C#根据网址生成静态页面
hvt
Web.netC#asp.nethovertree
HoverTree开源项目中HoverTreeWeb.HVTPanel的Index.aspx文件是后台管理的首页。包含生成留言板首页,以及显示用户名,退出等功能。根据网址生成页面的方法:
bool CreateHtmlFile(string url, string path)
{
//http://keleyi.com/a/bjae/3d10wfax.htm
stri
- SVG 教程 (一)
天梯梦
svg
SVG 简介
SVG 是使用 XML 来描述二维图形和绘图程序的语言。 学习之前应具备的基础知识:
继续学习之前,你应该对以下内容有基本的了解:
HTML
XML 基础
如果希望首先学习这些内容,请在本站的首页选择相应的教程。 什么是SVG?
SVG 指可伸缩矢量图形 (Scalable Vector Graphics)
SVG 用来定义用于网络的基于矢量
- 一个简单的java栈
luyulong
java数据结构栈
public class MyStack {
private long[] arr;
private int top;
public MyStack() {
arr = new long[10];
top = -1;
}
public MyStack(int maxsize) {
arr = new long[maxsize];
top
- 基础数据结构和算法八:Binary search
sunwinner
AlgorithmBinary search
Binary search needs an ordered array so that it can use array indexing to dramatically reduce the number of compares required for each search, using the classic and venerable binary search algori
- 12个C语言面试题,涉及指针、进程、运算、结构体、函数、内存,看看你能做出几个!
刘星宇
c面试
12个C语言面试题,涉及指针、进程、运算、结构体、函数、内存,看看你能做出几个!
1.gets()函数
问:请找出下面代码里的问题:
#include<stdio.h>
int main(void)
{
char buff[10];
memset(buff,0,sizeof(buff));
- ITeye 7月技术图书有奖试读获奖名单公布
ITeye管理员
活动ITeye试读
ITeye携手人民邮电出版社图灵教育共同举办的7月技术图书有奖试读活动已圆满结束,非常感谢广大用户对本次活动的关注与参与。
7月试读活动回顾:
http://webmaster.iteye.com/blog/2092746
本次技术图书试读活动的优秀奖获奖名单及相应作品如下(优秀文章有很多,但名额有限,没获奖并不代表不优秀):
《Java性能优化权威指南》
为
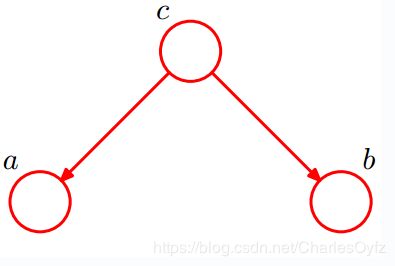
的父亲集合
![]()
,证明如下:
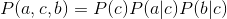

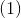
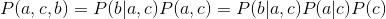
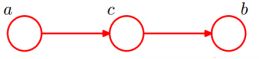
, 所以a与b独立:
,证明如下:
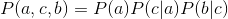
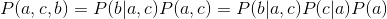
, 所以a与b独立:
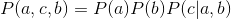
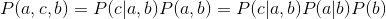
, 所以a与b独立: