论文阅读 Learning Affinity via Spatial Propagation Networks

abstract

通过一个空间传播网络来学习affinity matrix来用于vision tasks。实验证明，构造一个线性传播模型，空间上变换的affinity matrix可以用来建模图像密集和全局相似性。本文创建了一个three-way 连接的线性传播模型。该模型构造了一个所有元素均来自于DCNN的稀疏传播矩阵，同时创造了一个能用来建模任意特定任务的密集近邻矩阵。本文用data-driven manner来获取similarities，结果可以用在所有相似的图像任务上，包括但不限于图像分割。

---

Introduction

邻接矩阵是用来描述两个点有多近，多相似的。在高维空间任务也有作用，但是一直没有视作为一个可学习的问题。在这个paper里我们证明学习affinity matrix等价于学习一系列row/column wise空间上线性变换的矩阵。在这里，我们发现用three-way connection比用fully connection更有效地学习dense affinity matrix。

---

用data-driven manner学习affinity matrix的优势是多方面的（multifold）。1. 在低维空间的相似矩阵的assumption并不适用于mid-to-high-level。2. 可以学习高维的特征的affinity。

---

ralated work

略

---

proposed approach

SPN 能够转换一个2D map成一个新的拥有希望性质的map。这个过程等价于standard anisotropic diffusion process。图像转换相当于是经过laplacian matrix转化的。（从未见过如此数学化的dcnn论文）

数学证明 linear propagation as spatial diffusion

假设 X , H 是2D图像，大小是 n×n , xt,ht 是第 t 纵列。对于left-to-right的传播，有如下跟新规则。

ht=(I−dt)xt+ωtht−1(1)

I 是单位矩阵，初始化条件 h1=x1 ，以及 dt(i,i) 是对角矩阵， ith 元素是第i列 ωt 的和。

dt(i,i)=∑j=1,j≠inωt(i,j)(2)

.
即有：

Hν=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢Iω2ω2ω3⋮⋮0λ2ω3λ2⋮⋮...0λ3⋮⋯.........⋱⋯0......⋮λn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥Xν=GXν(3)

其中 λt=I−dt .

定理1

G 的每一行元素合起来等于1

定理2

对于演化矩阵 {U}T ，有 ∂TU=−LU ，L是拉普拉斯矩阵，D是degree矩阵，A是affinity matrix。
定理2证明了 (1)是一个标准的扩散过程， L 定义了空间传播， A 邻接矩阵描述了两个点之间的相似程度。所以学习 A 和学习 ω 是一样的。关键在于怎么让深度学习网络学习邻接矩阵。

learning data-driven affinity

因为邻接矩阵用来描述特定输入的图像的相似，所以肯定需要data有关。输入是 c 通道，输出是 n×c×4 通道。这个计算量太大，所以就证明了certain local connections可以实现。
然后证明了一波three-way connection更好。简而言之就是每一个pixel与前一个row/column的三个pixel连接比只连接一个pixel更好。

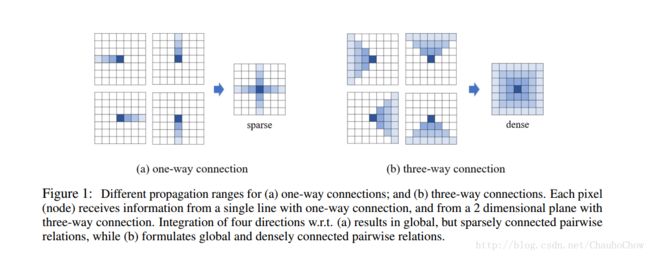
定理3

证明了该变换是stability的。

implementation

两个部分：
(a). 一个deep CNN输出transformation matrix。
(b). 一个线性传播module，输出propagation结果。

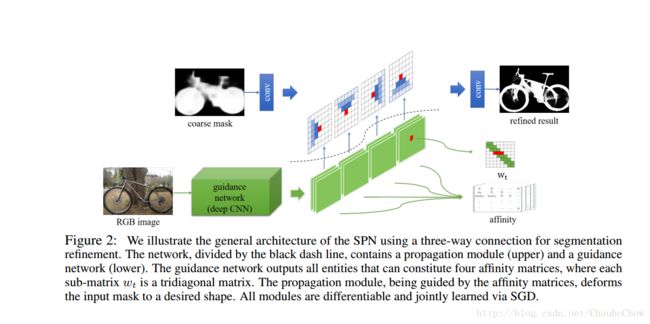
在deep CNN输入一张图像，大小为 n×n×n×c ，输出的就是 n×n×n×c×(3×4) 。
3个不同的点和4个传播方向

experimental results

SPN可以用来联合训练任意的segmentation model，作为一个refinement的工具。接下来就是测试的数据和流程。结果就是显著提高效果。

---

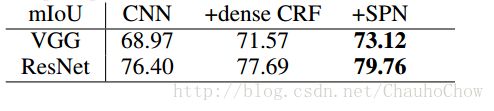
补充

引用来源于万能的知乎

https://www.zhihu.com/question/24591127

以及csdn博客

http://blog.csdn.net/Marco_L_T/article/details/72888138
http://blog.csdn.net/bluecol/article/details/46690985
http://blog.csdn.net/EbowTang/article/details/43016451

基本定义

一个图的邻接矩阵 G ：对于无向图的边 (u,v) ， G[u][v]++,G[v][u]++
一个图的度数矩阵 D ：对于无向图的边 (u,v) ， D[u][u]++,D[v][v]++
拉普拉斯矩阵为：

L=D−G

各向异性扩散，也叫做P–M扩散，在图像处理和计算机视觉中广泛用于保持图像细节特征的同时减少噪声。

各向异性扩散

连续性方程

以电磁理论的电荷守恒为例子，很容易有

∂ρ∂t+∇⃗ ⋅J⃗ =0

如果在空间中有一个浓度场 ρ(x,y,z,t) ，则浓度场（电场）中的电荷必然会向四周扩散，而且很容易明白，一定是从高浓度沿着低浓度方向扩散的，就是沿着梯度。很容易有扩散方程：

∂ρ∂t=∇⃗ (K⃗ ⋅∇⃗ ρ)

略去扩散系数，有

∂ρ∂t=∇⃗ (⋅∇⃗ ρ)=ρxx+ρyy+ρzz

直接的含义是在每个时间段内，如果一个点的二阶导数大于0，浓度增加，反之亦然。一直到 t→∞ ，整个场都变得光滑了。

散度在图像中的运用

同样地在图像中用梯度算子配合以连续性方程可以平滑图像。这就是用 I(x,y) 代替 ρ 。但是连续性方程式四向均匀的，所以就有个PM方程：
图像边缘在梯度值较大的点处，如果扩散房产在梯度值较大的区域减速扩散，在梯度值小的加速扩散，就可以去噪的同时又保护细节

∂I∂t=aIxx+bIyy,a>b

假设 xx 是平行于边缘方向， yy 是横跨边缘方向.



分别是原图，各向同性扩散图，各向异性扩散图

python参考代码

import numpy as np
import math
import scipy.ndimage
from scipy import misc as misc
np.set_printoptions(threshold=np.inf)
def anisodiff2d(image, num_iter, delta_t, kappa, activation):
    """
    :param image: 输入图像
    :param num_iter: 滤波次数
    :param delta_t: 积分常数 0 - 1 /7
    :param kappa: 梯度阈值
    :param activation: 扩散函数
    :return: 扩散图像
    """
    init_im = image
    # 初始矩阵

    dx = 1
    dy = 1
    dd = math.sqrt(2)
    # 距离

    lu = np.array([[1, 0, 0], [0, -1, 0], [0, 0, 0]])
    uu = np.array([[0, 1, 0], [0, -1, 0], [0, 0, 0]])
    ru = np.array([[0, 0, 1], [0, -1, 0], [0, 0, 0]])
    lm = np.array([[0, 0, 0], [1, -1, 0], [0, 0, 0]])
    rm = np.array([[0, 0, 0], [0, -1, 1], [0, 0, 0]])
    lb = np.array([[0, 0, 0], [0, -1, 0], [1, 0, 0]])
    mb = np.array([[0, 0, 0], [0, -1, 0], [0, 1, 0]])
    rb = np.array([[0, 0, 0], [0, -1, 0], [0, 0, 1]])
    # 八个方向的掩码

    for i in range(num_iter):
        nable_lu = scipy.ndimage.correlate(init_im, lu, mode= 'nearest')
        nable_uu = scipy.ndimage.correlate(init_im, uu, mode= 'nearest')
        nable_ru = scipy.ndimage.correlate(init_im, ru, mode= 'nearest')
        nable_rm = scipy.ndimage.correlate(init_im, rm, mode= 'nearest')
        nable_lm = scipy.ndimage.correlate(init_im, lm, mode= 'nearest')
        nable_lb = scipy.ndimage.correlate(init_im, lb, mode= 'nearest')
        nable_mb = scipy.ndimage.correlate(init_im, mb, mode= 'nearest')
        nable_rb = scipy.ndimage.correlate(init_im, rb, mode= 'nearest')

        c_lu = activation(nable_lu, kappa)
        c_uu = activation(nable_uu, kappa)
        c_ru = activation(nable_ru, kappa)
        c_rm = activation(nable_rm, kappa)
        c_lm = activation(nable_lm, kappa)
        c_lb = activation(nable_lb, kappa)
        c_mb = activation(nable_mb, kappa)
        c_rb = activation(nable_rb, kappa)

        init_im = init_im + delta_t * (
                (1 / (dd * dd)) * c_lu * nable_lu + (1 / (dy * dy)) * c_uu * nable_uu +
                (1 / (dd * dd)) * c_ru * nable_ru + (1 / (dx * dx)) * c_rm * nable_rm +
                (1 / (dx * dx)) * c_lm * nable_lm + (1 / (dd * dd)) * c_lb * nable_lb +
                (1 / (dy * dy)) * c_mb * nable_mb + (1 / (dd * dd)) * c_rb * nable_rb
                )
        print("*****complete {} iteration*******".format(i + 1))

    return init_im


def activation(nable, kappa):
    # return np.exp(-(nable / kappa)*(nable / kappa))
    return 1 / (1 + (nable / kappa) * (nable / kappa))


if __name__ == "__main__":
    image = misc.imread(r"ori.jpg", mode = "RGB")
    num_iter = 20
    delta_t = 1/7
    kappa = 20
    # a = image[0]
    print(np.shape(image[:,:,0]))
    image[:, :, 0] = anisodiff2d(image[:,:,0], num_iter, delta_t, kappa, activation)
    image[:, :, 1] = anisodiff2d(image[:,:,1], num_iter, delta_t, kappa, activation)
    image[:, :, 2] = anisodiff2d(image[:,:,2], num_iter, delta_t, kappa, activation)
    #ima = np.array([a.tolist(),b.tolist(),c.tolist()])

    # print(a - image[0])

    misc.imsave(r"new.jpg", image)

待继续填坑
跪求代码