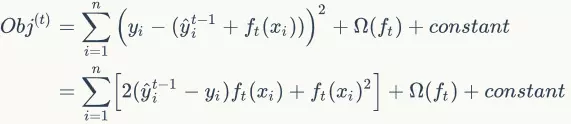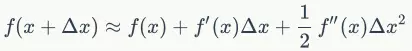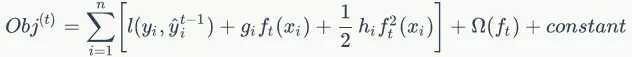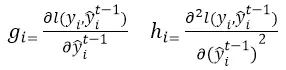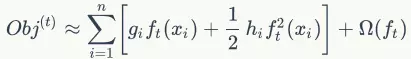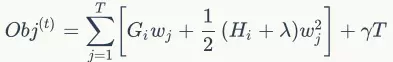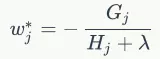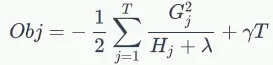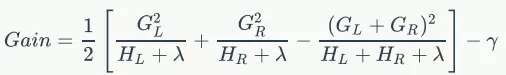XGBOOST学习实战
一.GBGT
参考见:
https://juejin.im/post/5a1624d9f265da43310d79d5
二 XGBOOST和GBDT区别
1.XGBoost比GBDT多了两项泰勒展开式
XGBoost算法可以看成是由K棵树组成的加法模型:
XGBoost加法模型
其中F为所有树组成的函数空间(这里的回归树也就是一个分段函数,不同分段的不同取值就构成了一颗树),与一般机器学习算法不同的是,加法模型不是学习d维空间的权重,而是直接学习决策树的集合。
上述加法模型的目标函数定义为:
目标函数
其中Ω表示决策树的复杂度,那么该如何定义树的复杂度呢?比如,可以考虑树的节点数量、树的深度或者叶子节点所对应的分数的L2范数等等。
如何来学习加法模型呢?
解这一优化问题,可以用前向分布算法(forward stagewise algorithm)。有了之前GBDT的基础,我们知道,加法模型的学习器每次都用函数来拟合上一棵树没有拟合完整的残差,最后将这些残差全部加起来就会得到对于目标完整的预测,这也叫做Boosting。具体地,我们从一个常量预测开始,每次学习一个新的函数,过程如下:
加法学习器的Boosting
这就会产生一个新的问题,那个新加入的函数f到底怎么得到的呢?这个原则还是最小化目标函数。我们可以将我们的目标函数写为:
目标函数变式
我们再用平方误差来衡量我们的损失函数:
平方误差衡量损失函数
其中 ![]() 就是我们所谓的残差(residual)。我们每一次使用平方函数的时候,算法都是为了拟合这个残差。
就是我们所谓的残差(residual)。我们每一次使用平方函数的时候,算法都是为了拟合这个残差。
可能对于泰勒公式不是非常熟悉,将基本的泰勒公式用法写在这:
泰勒公式基本形式
泰勒级数展开其实是有无穷多项的,在无穷多项形式里是严格等于,这里我们暂且只取了前三项省略了后面,所以就是约等于。
那有了泰勒公式的基础,我们将前面的目标函数变式可以转化为:
目标函数泰勒级数展开三项
其中,g与h分别是损失函数的一阶偏导数和二阶偏导数,具体数学形式如下:
泰勒展开的一次微分项与二次微分项
我们也可以将常数项直接去掉,并不会影响,那就使得目标函数是这个样子:
去掉常数项的目标函数
由于要学习的函数仅仅依赖于目标函数,从“去掉常数项的目标函数”可以看出只需为学习任务定义好损失函数,并为每个训练样本计算出损失函数的一阶导数和二阶导数,通过在训练样本集上最小化目标函数即可求得每步要学习的函数,从而根据加法模型可得最终要学习的模型
GBDT的目标函数
GBDT与XGBoost的区别,明显可以看出,GBDT没有采用二次泰勒展开,这个看似很简单的区别,实际上带来更快的拟合,也大大缩减了生成树的规模,减少了运行时间。
XGBoost相比于GBDT加入了正则化项(Regularization):
我们使用损失函数优化是为了避免欠拟合,而使用正则化项就是为了避免过拟合。正则化项与损失函数共同组成了我们的目标函数。XGBoost比GBDT多添加了以树复杂度构成的正则化项,也是XGBoost实际表现更为优秀的原因之一
我们假设XGBoost决策树的叶子节点个数为T,该决策树是由所有叶子节点对应的值组成的向量w,以及一个把特征向量映射到叶子节点索引(Index)的函数 ![]() 组成的,我们将树可以写成:
组成的,我们将树可以写成:![]() ,我们也可以将决策树的复杂度定义成正则项:
,我们也可以将决策树的复杂度定义成正则项:
决策树复杂度定义的正则化项
则目标函数我们可以写成:
完整正则项的目标函数
用G与H代换一下原来的式子,我们就得到了简化后的式子:
简化后的目标函数
假设树的结构是固定的,即函数q(x)为固定的,令目标函数的一阶导数为0,则可以求出叶子节点j对应的值为:
叶子节点j对应的值
于是在这种条件下,目标函数的值就变成了:
目标函数的值
为什么要计算这两个值呢?
是为了给大家描述单棵决策树的生成过程:
- 枚举所有可能的树的结构q
- 用目标函数值为每个q计算对应的分数Obj,分数越小说明结构越好
- 根据上一步结果,找到分数最小的子节点,生成新的分支,并为每个子节点计算预测值
XGBoost的分裂增益与GBDT的比较
树结构数量是无穷的,所以实际上我们不可能枚举所有可能的树结构。通常情况下,我们采用贪心策略来生成决策树的每个节点。
我们来看看这个贪心算法是怎么工作的:
- 从深度为0的树开始,对每个叶节点枚举所有的可用特征
- 针对每个特征,把属于该节点的训练样本根据该特征值升序排列,通过线性扫描的方式来决定该特征的最佳分裂点,并记录该特征的最大收益(采用最佳分裂点时的收益)
- 选择收益最大的特征作为分裂特征,用该特征的最佳分裂点作为分裂位置,把该节点生长出左右两个新的叶节点,并为每个新节点关联对应的样本集
- 回到第1步,递归执行到满足特定条件为止
如何计算每次分裂的收益呢?假设当前节点记为C,分裂之后左孩子节点记为L,右孩子节点记为R,则该分裂获得的收益定义为当前节点的目标函数值减去左右两个孩子节点的目标函数值之和:Gain=ObjC-ObjL-ObjR,具体地,根据目标函数值公式可得:
XGBoost的增益
三.XGBOOST和GBDT的不同
参考链接:https://juejin.im/post/5a13c9a8f265da43333e0648
xgboost相比传统gbdt有何不同?xgboost为什么快?xgboost如何支持并行?
看了陈天奇大神的文章和slides,略抒己见,没有面面俱到,不恰当的地方欢迎讨论:
- 传统GBDT以CART作为基分类器,xgboost还支持线性分类器,这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归(分类问题)或者线性回归(回归问题)。
- 传统GBDT在优化时只用到一阶导数信息,xgboost则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。顺便提一下,xgboost工具支持自定义代价函数,只要函数可一阶和二阶求导。
- xgboost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
- Shrinkage(缩减),相当于学习速率(xgboost中的eta)。xgboost在进行完一次迭代后,会将叶子节点的权重乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。实际应用中,一般把eta设置得小一点,然后迭代次数设置得大一点。(补充:传统GBDT的实现也有学习速率)
- 列抽样(column subsampling)。xgboost借鉴了随机森林的做法,支持列抽样,不仅能降低过拟合,还能减少计算,这也是xgboost异于传统gbdt的一个特性。
- 对缺失值的处理。对于特征的值有缺失的样本,xgboost可以自动学习出它的分裂方向。
- xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的?注意xgboost的并行不是tree粒度的并行,xgboost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。xgboost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),xgboost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
- 可并行的近似直方图算法。树节点在进行分裂时,我们需要计算每个特征的每个分割点对应的增益,即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以xgboost还提出了一种可并行的近似直方图算法,用于高效地生成候选的分割点。
四.XGBOOST的API参数
XGBoost参数:
gbm = xgb.XGBClassifier(silent=1, max_depth=10, n_estimators=1000, learning_rate=0.05)
max_depth=3, 这代表的是树的最大深度,默认值为三层。max_depth越大,模型会学到更具体更局部的样本。
learning_rate=0.1,学习率,也就是梯度提升中乘以的系数,越小,使得下降越慢,但也是下降的越精确。
n_estimators=100,也就是弱学习器的最大迭代次数,或者说最大的弱学习器的个数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,计算量会太大,并且n_estimators到一定的数量后,再增大n_estimators获得的模型提升会很小,所以一般选择一个适中的数值。默认是100。
silent=True,是我们训练xgboost树的时候后台要不要输出信息,True代表将生成树的信息都输出。
objective="binary:logistic",这个参数定义需要被最小化的损失函数。最常用的值有:
binary:logistic二分类的逻辑回归,返回预测的概率(不是类别)。multi:softmax使用softmax的多分类器,返回预测的类别(不是概率)。在这种情况下,你还需要多设一个参数:num_class(类别数目)。multi:softprob和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率。
nthread=-1, 多线程控制,根据自己电脑核心设,想用几个线程就可以设定几个,如果你想用全部核心,就不要设定,算法会自动识别
gamma=0,在节点分裂时,只有分裂后损失函数的值下降了,才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大,算法越保守。这个参数的值和损失函数息息相关,所以是需要调整的。
min_child_weight=1,决定最小叶子节点样本权重和。 和GBM的 min_child_leaf 参数类似,但不完全一样。XGBoost的这个参数是最小样本权重的和,而GBM参数是最小样本总数。这个参数用于避免过拟合。当它的值较大时,可以避免模型学习到局部的特殊样本。 但是如果这个值过高,会导致欠拟合。这个参数需要使用CV来调整
max_delta_step=0, 决定最小叶子节点样本权重和。 和GBM的 min_child_leaf 参数类似,但不完全一样。XGBoost的这个参数是最小样本权重的和,而GBM参数是最小样本总数。这个参数用于避免过拟合。当它的值较大时,可以避免模型学习到局部的特殊样本。 但是如果这个值过高,会导致欠拟合。这个参数需要使用CV来调整。
subsample=1, 和GBM中的subsample参数一模一样。这个参数控制对于每棵树,随机采样的比例。减小这个参数的值,算法会更加保守,避免过拟合。但是,如果这个值设置得过小,它可能会导致欠拟合。典型值:0.5-1
colsample_bytree=1, 用来控制每棵随机采样的列数的占比(每一列是一个特征)。典型值:0.5-1
colsample_bylevel=1,用来控制树的每一级的每一次分裂,对列数的采样的占比。其实subsample参数和colsample_bytree参数可以起到相似的作用。
reg_alpha=0,权重的L1正则化项。(和Lasso regression类似)。可以应用在很高维度的情况下,使得算法的速度更快。
reg_lambda=1, 权重的L2正则化项这个参数是用来控制XGBoost的正则化部分的。这个参数越大就越可以惩罚树的复杂度
scale_pos_weight=1,在各类别样本十分不平衡时,把这个参数设定为一个正值,可以使
base_score=0.5, 所有实例的初始化预测分数,全局偏置;为了足够的迭代次数,改变这个值将不会有太大的影响。
seed=0, 随机数的种子设置它可以复现随机数据的结果,也可以用于调整参数
五.实战
题:https://tianchi.aliyun.com/competition/entrance/231620/introduction
代码:
import pandas as pd
import xgboost as xgb
from sklearn import preprocessing
train = pd.read_csv(r'D:\ML\train.csv')
tests = pd.read_csv(r'D:\ML\test.csv')
#把时间转化为日期,再转化为多个时间特征
train['time_stamp'] = pd.to_datetime(pd.Series(train['time_stamp']))
tests['time_stamp'] = pd.to_datetime(pd.Series(tests['time_stamp']))
train['Year'] = train['time_stamp'].apply(lambda x:x.year)
train['Month'] = train['time_stamp'].apply(lambda x: x.month)
train['weekday'] = train['time_stamp'].apply(lambda x: x.weekday())
train['time'] = train['time_stamp'].dt.time
tests['Year'] = tests['time_stamp'].apply(lambda x: x.year)
tests['Month'] = tests['time_stamp'].apply(lambda x: x.month)
tests['weekday'] = tests['time_stamp'].dt.dayofweek
tests['time'] = tests['time_stamp'].dt.time
# traind丢掉有缺失值的数据 ,补上test缺失值
train = train.drop('time_stamp', axis=1)
train = train.dropna(axis=0)
tests = tests.drop('time_stamp', axis=1)
tests = tests.fillna(method='pad')
#把数据变成标签化
for f in train.columns:
if train[f].dtype=='object':
if f != 'shop_id':
print(f)
lbl = preprocessing.LabelEncoder()
train[f] = lbl.fit_transform(list(train[f].values))
for f in tests.columns:
if tests[f].dtype == 'object':
print(f)
lbl = preprocessing.LabelEncoder()
lbl.fit(list(tests[f].values))
tests[f] = lbl.transform(list(tests[f].values))
# 将train和tests转化成matrix类型
feature_columns_to_use = ['Year', 'Month', 'weekday',
'time', 'longitude', 'latitude',
'wifi_id1', 'wifi_strong1', 'con_sta1',
'wifi_id2', 'wifi_strong2', 'con_sta2',
'wifi_id3', 'wifi_strong3', 'con_sta3',
'wifi_id4', 'wifi_strong4', 'con_sta4',
'wifi_id5', 'wifi_strong5', 'con_sta5',
'wifi_id6', 'wifi_strong6', 'con_sta6',
'wifi_id7', 'wifi_strong7', 'con_sta7',
'wifi_id8', 'wifi_strong8', 'con_sta8',
'wifi_id9', 'wifi_strong9', 'con_sta9',
'wifi_id10', 'wifi_strong10', 'con_sta10',]
big_train = train[feature_columns_to_use]
big_test = tests[feature_columns_to_use]
train_X = big_train.as_matrix()
test_X = big_test.as_matrix()
train_y = train['shop_id']
# XGBT决策树
gbm = xgb.XGBClassifier(silent=1, max_depth=10,
n_estimators=1000, learning_rate=0.05)
gbm.fit(train_X, train_y)
predictions = gbm.predict(test_X)
# 提取预测数据
submission = pd.DataFrame({'row_id': tests['row_id'],
'shop_id': predictions})
print(submission)
submission.to_csv("submission.csv",index=False)