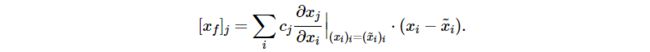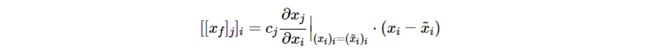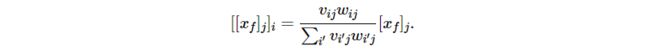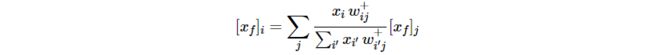A Quick Introduction to Deep Taylor Decomposition

 本文介绍了下面这篇文章描述的深度泰勒分解法的主要思想：

G. Montavon, S. Lapuschkin, A. Binder, W. Samek, K.-R. Müller
Explaining NonLinear Classification Decisions with Deep Taylor Decomposition
Pattern Recognition, 65:211–222, 2017

1. Introduction

深度泰勒分解是一种用输入变量来解释单个神经网络预测的方法。它通过使用预定义的规则集在网络上运行向后传递来操作。其结果是对输入变量的神经网络输出进行分解。该方法可以作为可视化工具使用，也可以作为更复杂的分析途径的一部分。例如，深度泰勒分解被用来解释最先进的计算机视觉神经网络。

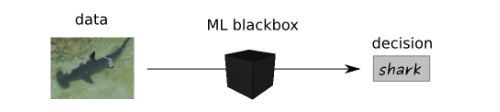
在深入研究深度泰勒分解的数学方面之前，我们将首先从概念上研究解释问题，并考虑由机器学习分类器预测的属于“shark”类的图像的简单示例。

例如，机器学习分类器可以是卷积神经网络，如AlexNet或GoogleNet。当训练后的模型得到一幅图像时，它提供了对该图像的预测，但没有相关的解释。

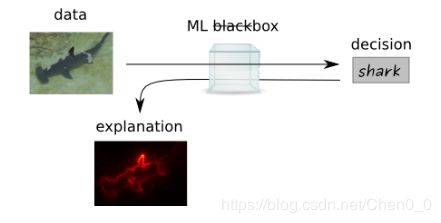
通过确定哪些输入变量(这里是像素)对图像分类有贡献，特别是图像中哪些像素与预测结果相关，可以得到一种可能的解释。我们把分数赋值到像素上称为热图。这样的热图可以可视化为与要分类的图像大小相同的图像。

在热图中，图像的相关部分用红色高亮显示。这里，我们认为鲨鱼及其背鳍的轮廓与分类有关。因此，机器学习模型不再是黑盒。

1.1 Sensitivity vs. decomposition

分析神经网络预测的一种简单方法是基于梯度的灵敏度分析。在最简单的形式中，它计算给定数据点的神经网络输出函数相对于输入变量的梯度。在上面的例子中，梯度会告诉我们，如果改变颜色，图像中的哪些像素会使图像更像或不像鲨鱼。然而，我们对以下两个问题进行了区分：

1. "What makes the shark less/more a shark"
2. "What makes the shark a shark"

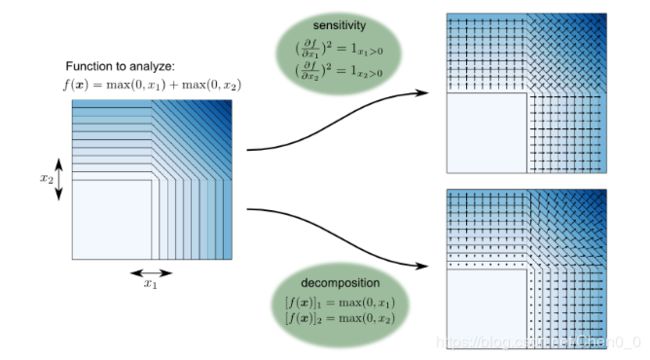
第二个问题最好由分解技术来回答。分解的目的是将整个预测的输出重新分配到输入像素上。因此，分解技术试图从整体上解释预测，而不仅仅是测量差异效应。通过一个简单的二维例子(两个非线性函数的和，每个函数作用于输入空间的一个变量)，可以更容易地理解灵敏度和分解之间的差异。

蓝色区域函数值较高，白色区域函数值为零。向量场表示在输入空间的不同位置上分析的每个组件的大小。我们可以观察到，敏感性和分解导致定性上非常不同的结果：

灵敏度分析在输入空间的象限之间产生不连续:两个任意闭合点可能具有明显不同的箭头方向。其次，对于输出值大的点和输出值小的点，甚至对于输出值无穷小的点，分析都给出了相同的解释。

在输入域中，分解是连续的，输入空间中相邻的两个点总是有类似的解释(假设函数是连续的)。此外，分解的大小(箭头的大小)与空间中给定点的函数值成正比。

总而言之，敏感性分析度量局部效应，而分解度量全局效应。灵敏度分析和分解方法都具有加性结构。灵敏度分析满足方程

其中，左手边对所有输入变量求和(即分析将全部局部函数变化重新分配到输入变量)。同样，分解方法必须满足方程

(即整个函数值需要重新分布在输入变量上)。在实践中，为了避免(9999)+(10000)= 1类型的分解，我们希望对分解后的项执行一个额外的正性约束，其中分解后的项的大小可以变得任意高。注意，敏感性分析已经通过平方函数在结构上包含了这种约束。

2. The deep Taylor decomposition method

在前一节中，我们已经解释了分解分析在概念上与敏感性分析有何不同，以及为什么在解释预测问题时应该首选分解。本节介绍深度泰勒分解，这是最近提出的一种分解大型深度神经网络预测的实用方法。

该方法的灵感来自于误差反向传播的工作方式:(1)将整个计算分解为一组局部神经元计算，(2)以适当的方式重新组合这些局部计算(对于误差反向传播，使用导数链式法则)。

我们考虑一个深网络，其中表示输入神经元，表示输出神经元。我们想用输入变量对输出进行分解，其中是分配给特定输入变量的函数值的份额。分解应满足守恒性质

and

我们采用一种传播方法来解决这个问题，其中中间神经元被分配了的一部分，并且必须将这个量重新分配到它们的前一个神经元上。从全局来看，这种再分配过程导致了神经网络输出到输入变量的分解。

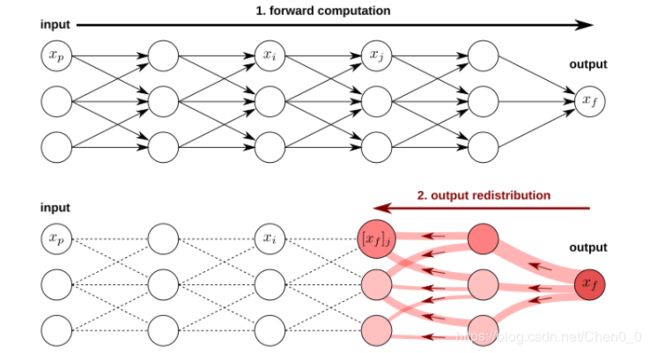
2.1 Backpropagating function value

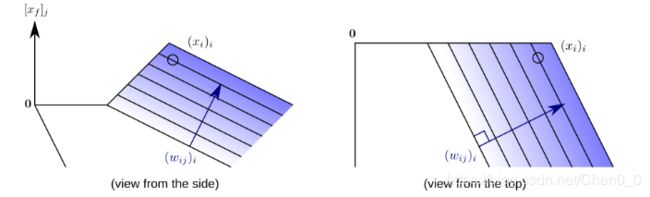
假设我们已经计算了一个正向传递中的所有激活，并且我们已经将神经网络输出从顶层重新分配到与神经元xj相关的层。该场景如下图所示

我们用xj表示网络中的任意一个神经元，(xi)i表示它接收到的作为输入的神经元集合。我们的问题是，与这个神经元相关的函数值[xf]j的哪一部分应该重新分配到上一层的每个神经元(xi)i。我们表示这些分配[[xf]j]i。这个问题是困难的，因为先验上没有已知的直接映射(xi)i—>[xf]j，我们可以从中得到一个分解策略。相反，我们将假设[xf]j总是可以表示为神经元激活xj和一个正的局部常数项cj0的乘积:

变量cj可以解释为激活xj对局部神经网络输出的影响程度。注意，顶层神经元xf很容易具有这种乘积结构。这种产生的结构的优点是,分解问题本质上降低了分解函数,我们知道,在下一节中,我们将展示产生分解所需的属性。重要的是，这个神经元函数分解后的重分布也应该产生乘积结构的分解项，这样通过归纳推理，函数值可以通过任意多个层进行反向传播。

2.2 Local decomposition through Taylor expansion

在本节中，我们描述了一种基于泰勒展开的ReLU神经元可能的传播机制。传播机制确保了分解所需的属性(可加性和分解项的正性)，并保证传播项的积结构从一层到前一层近似保留(向后传播的必要条件)。

我们考虑给定的ReLU神经元通过非线性函数从其输入映射到其重分布函数值

其中，cj在相关域中为正且为常数。我们想分解输入神经元上的。下面是一个二维输入域的函数

通过观察这个图，我们注意到函数在集合上是线性的。如果在这个集合的边界上选择一个点，称之为“根点”，在这里函数是无穷小的，那么函数总是可以写成一阶泰勒展开式

没有零阶项，也没有二阶项或高阶项。通过识别各输入变量的和的元素，我们得到了对输入变量的分解

2.3 From root points to search directions

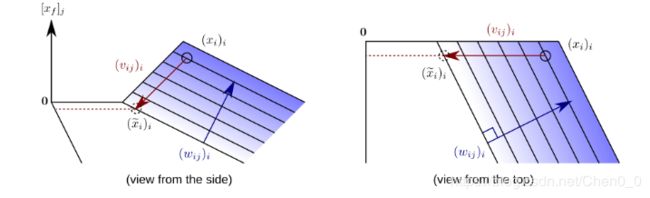
实际上，没有必要显式地定义这个根点。相反,原始论文深度泰勒分解表明,我们总是可以隐含地表达神经元激活的根点，因为平面方程的交点表示所有可能的根源点，和一个“搜索方向”，实际神经元输入。根点与搜索方向的关系如下图所示

分解后的项以封闭形式给出

最后，神经元接收来自它所贡献的许多神经元的消息。因此，得到的的总份额由

2.4 Narrowing down the space of possible decompositions

在实际应用中，对分解后的项施加了许多约束，限制了可能的搜索方向集合。对于除输入层之外的所有层，约束如下

Domain:执行泰勒展开的根点必须位于神经元输入域内。例如，当神经元作为输入接收到其他ReLU神经元的输出时，输入域变为正值，因此根点的所有组件也必须为正值。因此，可能的搜索方向集相应地减少。

Positivity: 应用分解法得到的热图应该是正的，这是由于各种原因被认为是可取的。保证热图的正性的一个充分条件是在神经元水平上加强这一特性。实际上，这可以通过在再分配公式中强制所有产品为正来实现。

Product:为了支持向后传播，重新分布的项必须具有结构，且在相关域中，近似为常数。这可以通过选择的线性搜索方向来实现，从而使产品结构出现。

这些方面在原文中有更详细的讨论。实际上，搜索方向同时满足所有这些条件。选择它就得到了传播规则

叫做rule。对于第一层，需要满足的约束略有不同，这导致了不同的重新分配规则。这些具体的规则在原文中给出。