DeepSeek + 药物研发:解决药物研发周期长、成本高-降低80%、失败率高-减少40%
DeepSeek + 药物研发:解决药物研发周期长、成本高-降低80%、失败率高-减少40%
- 论文大纲
- 1. WHY —— 研究背景与现实问题
- 1.1 研究要解决的现实问题与提出背景
- 1.2 研究所要解决的问题类别
- 1.3 正反例对比
- 关联:和前人的工作有什么关系?
- 3. 总结归纳
- 3.1 总结收获
- 3.2 探索思考
- 4. WHAT —— 核心发现或论点
- 5. HOW —— 研究过程、创新与关键数据
- 6. HOW GOOD —— 理论贡献与实践意义
- 解法拆解
- 1.1 主解法整体逻辑
- 1.2 进一步拆解「主解法」为子解法
- 1.3 每个子解法与“溶出模型”的对应关系
- 2. 这些子解法是什么样的逻辑链?(以决策树形式列出)
- 3. 分析是否有隐性方法
- 4. 分析是否有隐性特征
- 5. 方法可能存在哪些潜在的局限性
- 提示词
论文:DeepSeek Powered Solid Dosage Formulation Design and Development
论文大纲
├── 1 引言【阐述研究背景与需求】
│ ├── 制药过程设计和开发复杂且耗时【背景:多阶段评估,质量控制严格】
│ ├── 传统依赖经验知识,流程冗长且成本高【问题:25-40%后期失败,投入巨大】
│ ├── 急需新的方法来系统化知识、降低成本、提升效率【需求:加速药物配方与临床试验】
│ └── 大模型(LLMs)有望整合文献和实验数据,加速药物研发【关键创新:从经验到数据驱动】
├── 2 现有方法与挑战【已有技术手段与局限】
│ ├── 传统计算模拟(如DEM、FEA)【局限:对多参数系统描述不充分,理想化假设较多】
│ ├── 机器学习(ML)方法【局限:需大量标注数据,易受训练数据规模和质量限制】
│ └── 整合文献知识与实验数据不足,无法全面解决【问题:碎片化与缺乏一体化平台】
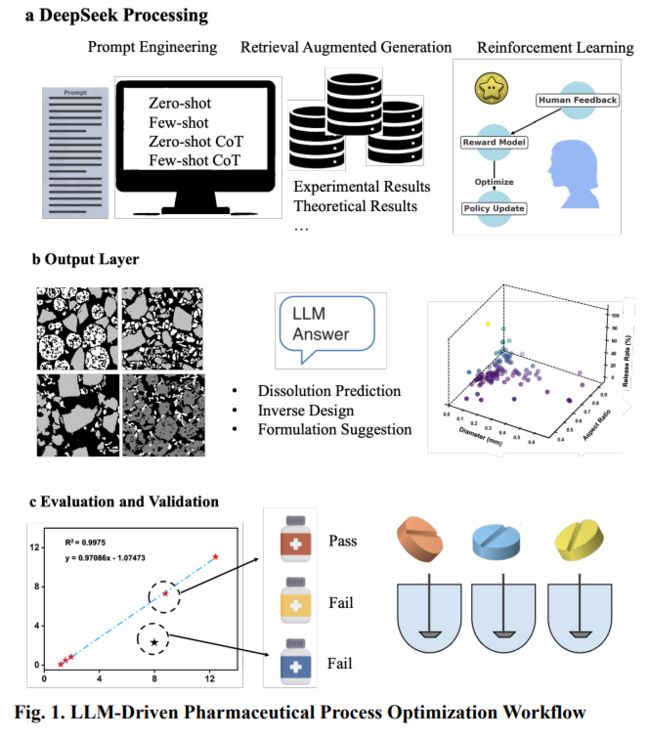
├── 3 大模型DeepSeek及其工作流程【介绍LLM及设计思路】
│ ├── DeepSeek-R1-671b【模型规模:6710亿参数,多模态适应性强】
│ ├── 提示工程(Prompt Engineering)【思路:结构化提示,串联物理模型与监管要求】
│ │ ├── Zero-shot与Few-shot【概念:无示例或少量示例的提示方式】
│ │ ├── Chain-of-Thought (CoT)【概念:分步推理,降低推理错误】
│ │ └── 结合提示示例与算力,减少“幻觉”【目标:提升模型对复杂任务的准确性】
│ ├── 需求驱动:溶出度曲线预测与逆向设计【核心任务:从粒径、溶解度等参数推算或设计】
│ └── 检索增强生成 (RAG) 与人类反馈强化学习 (RLHF)【方法:调用外部文献数据库并结合人工反馈】
├── 4 药物溶出实验与验证【实验设计与评估方式】
│ ├── USP II Paddle方法测定药物溶出【实验条件:pH 7.2和pH 6.2,保证一致性】
│ ├── UV-Vis用于检测药物浓度【实验手段:光度计分析溶出度】
│ ├── 重复实验确保数据可靠性【统计学要求:五次以上平行实验】
│ └── 建立评价指标【MSE和R²用于量化模型预测与真实数据的偏差】
├── 5 实验结果与讨论【模型预测结果对比】
│ ├── 提示工程的比较【Zero-shot, Few-shot, CoT, RAG】
│ │ ├── Zero-shot:基线准确率高,但可能产生简单误差【MSE=23.61,R²=0.97】
│ │ ├── Zero-shot CoT:分步推理若无外部实例易出现“幻觉”【MSE=114.89,R²=0.90】
│ │ ├── Few-shot:有示例但未充分利用外部知识【MSE=57.0,R²=0.92】
│ │ ├── Few-shot CoT:结合少量示例与分步推理【MSE=22.56,R²=0.97】
│ │ └── RAG:整合外部数据,得到最佳性能【MSE=10.55,R²=0.99】
│ ├── 结果显示RAG最优【结论:外部文献与数据库检索显著提升模型精度】
│ └── 分析CoT和示例的作用【说明:示例可有效锚定模型推理路径,减少胡乱推断】
├── 6 面临的挑战与未来展望【问题总结与潜在改进方向】
│ ├── 数据获取与质量限制【挑战:药物溶出与粒径数据稀缺且不公开】
│ ├── 监管与可解释性需求【挑战:黑箱模型难获监管机构信任】
│ ├── 建立自有数据库+模拟数据【未来:30%实测+70%模拟,扩充训练与检索数据】
│ ├── 扩展至流动性与机械强度等重要性质【未来:构建更全面的物性和质量控制参数】
│ └── 跨学科协作与模型透明度提升【趋势:在药学、工程和AI领域交叉共建,保证结果可追溯性】
└── 7 结论【综合总结】
├── LLM与提示工程可加速药物配方设计【价值:实现快速溶出预测与逆向设计】
├── 深度检索与人类反馈能显著增强模型可靠性【重点:RAG与RLHF的应用】
└── 建议持续迭代模型与完善实验数据,以实现更广泛场景应用【方向:不断收敛与优化,迈向个性化医药】
核心方法:
├── 1 输入【模型所需的关键信息】
│ ├── 1.1 物理化学参数【用于溶出预测与逆向设计】
│ │ ├── 粒径分布 (PSD)、平均粒径 (D50)、体积当量粒径【描述颗粒大小特征】
│ │ ├── 形貌参数 (Aspect ratio、Roundness)【用于表征颗粒几何形态】
│ │ ├── 药物溶解度 (Solubility)、扩散系数 (Diffusion coefficient)【决定溶出速率】
│ │ ├── 密度 (True Density)、比表面积 (SSA)【影响药物溶出与传质特性】
│ │ └── 实验条件 (pH、搅拌速度等)【确定溶出测试或模拟环境】
│ └── 1.2 目标溶出曲线/目标释放度【若做逆向设计则需给定目标需求】
├── 2 处理过程【将输入信息整合到大模型进行预测与优化】
│ ├── 2.1 提示工程 (Prompt Engineering)【用来指导LLM生成更准确的结果】
│ │ ├── 2.1.1 结构化提示 (Structured Prompt Templates)【将监管要求与物化模型融入提示】
│ │ │ ├── 结合USP规范、Nernst-Brunner方程、径向扩散模型【保证科学约束】
│ │ │ └── 指定输出格式 (JSON/表格)【便于读取与后续比较】
│ │ ├── 2.1.2 Zero-shot & Few-shot【用于不同场景下的模型启动】
│ │ │ ├── Zero-shot【模型无示例直接推理,快速但易有偏差】
│ │ │ └── Few-shot【提供真实样例,帮助模型对齐实验或文献数据】
│ │ └── 2.1.3 Chain-of-Thought (CoT)【引导模型逐步推理,降低“幻觉”】
│ │ ├── Zero-shot CoT【模型自行拆分推理步骤】
│ │ └── Few-shot CoT【示例+步骤分解,最大程度保证推理合理】
│ ├── 2.2 检索增强生成 (Retrieval-Augmented Generation, RAG)【用来调用外部数据库或文献】
│ │ ├── 从专利库、FDA数据库、相关文献实时检索【获取真实溶出曲线或实验参数】
│ │ └── 将检索到的信息嵌入Prompt【减少模型凭空编造,增强预测可信度】
│ ├── 2.3 强化学习 (Reinforcement Learning)【用来进一步优化模型输出】
│ │ ├── 人类反馈强化学习 (RLHF)【实验人员或专家打分,模型迭代更新】
│ │ └── 结合奖励模型 (Reward Model)【对输出质量好坏进行度量,驱动模型学习】
│ └── 2.4 溶出度预测或逆向设计流程【将LLM预测和化学原理相结合】
│ ├── 根据输入参数,模型给出溶出度-时间曲线【预测:在不同时间点的释放百分比】
│ └── 若输入为目标曲线,模型反推关键颗粒参数【逆向设计:给出D50、SSA等建议值】
├── 3 输出【最终结果与评价指标】
│ ├── 3.1 溶出曲线预测表格或图像【输出在各时间点的溶出百分比】
│ ├── 3.2 逆向设计的颗粒参数推荐【若目标为特定溶出度,返回满足要求的PSD、SSA等】
│ ├── 3.3 误差度量 (MSE, R²)【用来评估模型预测与真实数据的吻合度】
│ └── 3.4 优化后的提示或参数设置【若偏差大,可根据反馈再次迭代Prompt或调整实验设计】
└── 4 各步骤衔接【明确方法之间的关系】
├── 输入→提示工程【【提供数据】供LLM读取;【指定格式】约束输出】
├── 提示工程→RAG【【调用外部数据】减少幻觉;【增强上下文】提高科学性】
├── RAG→RLHF【【结合检索信息】模型生成结果;【人类打分】强化学习优化】
├── RLHF→溶出预测与逆向设计【【动态调优模型】使预测更精准;【输出可循环迭代】】
└── 最终输出→指标评估【【对比实验结果】判断可行性;【继续迭代】若精度不够】
1. WHY —— 研究背景与现实问题
1.1 研究要解决的现实问题与提出背景
- 现实问题:制药行业的固体制剂研发流程普遍存在研发周期长、成本高、试验步骤繁琐以及质量控制要求严苛等困难。开发新药或改良仿制药往往需要大量资源投入,却依然面临较高的失败率。
- 研究背景:传统的制药过程开发严重依赖经验式试验或局限于对单参数的简化模拟;相对缺乏对多变量耦合、复杂机理的系统性掌握。随着大模型(LLMs)的发展,研究者希望借助其对大量文献与数据的“理解”与“推理”能力,为研发过程带来新的自动化、智能化工具。
1.2 研究所要解决的问题类别
- 类别:本研究聚焦在“药物固体制剂配方设计及其过程优化”这一范畴,主要针对颗粒尺寸分布、药物溶解度等多维参数对药物溶出曲线的影响。
- 具体问题:如何快速、准确地预测并设计不同参数组合下的药物溶出行为,达到缩短研发周期、降低失败风险的目标。
1.3 正反例对比
-
正例(成功应用的类比)
在材料科学领域,已有研究者成功使用大模型来预测材料结构、合成工艺等。例如,金属有机框架(MOF)的结构筛选中,LLMs的检索与推理大幅加速了实验设计,减少了大量人力与时间。
启示:类似的方法也可应用于药物制剂,从而加速对潜在配方和工艺的筛选。 -
反例(传统方法的不足)
药企在研发新型片剂时,往往依赖试错式实验:先根据经验设计几种配方,再逐一试验溶出度、稳定性,如果结果不理想则继续调整。这种方法周期长、成本高,不具备快速反应能力。
教训:传统方法在面对多变量耦合以及严格的质量标准时,效率极其低下,无法充分应对复杂的制剂要求。
关联:和前人的工作有什么关系?
- 具体关联:
- 与传统离散元或有限元模拟:将机理模型(Nernst-Brunner、径向扩散等)嵌入大模型提示中,弥补了仅靠物理模拟时多参变量难耦合的不足。
- 与机器学习方法:ML需要大量标注数据,LLM则能借助大规模语料和检索库,更快速掌握跨学科知识、降低对大规模标签的依赖。
3. 总结归纳
3.1 总结收获
- 核心观点:借助大模型的推理能力与人类反馈强化机制,可以在药物配方设计中更灵活、准确地预测溶出度,并大幅缩减研发阶段的试错成本。
- 方法亮点:提示工程(Prompt Engineering)+ RAG(检索增强)+ RLHF(强化学习)相结合,克服了传统ML或纯理论模拟的弊端,实现了对多参数、多场景的快速评估。
3.2 探索思考
- LLM在药物溶出领域遇到的主要挑战是什么?
- 如何保证模型推理结果的可解释性,以满足药监机构对药品质量与安全的审核?
- 当药物粒径或溶解度超出文献常见范围时,模型还能保持高精度吗?若不行,怎样改进?
4. WHAT —— 核心发现或论点
- 核心发现:
- LLM能通过零样本、少样本学习以及检索增强的方式,快速生成与真实实验近似的溶出度-时间曲线,预测准确度(R²)可高达0.99。
- 当给定目标溶出曲线(如FDA规定60分钟内溶出度≥85%),模型可以反向推断需要满足的粒径、比表面积、形状因子等物化参数。
- RAG与RLHF对模型精度的提升显著:在与真实实验比对中,MSE最低可达10.55。
5. HOW —— 研究过程、创新与关键数据
-
前人研究的局限性
- 传统仿真(DEM、FEA)高计算量且不易处理多变量;
- 普通ML对数据需求庞大,且无法灵活对接最新文献信息;
- “经验+试错”方式成本高昂。
-
创新是什么/视角
- 将提示工程(Prompt Engineering)与制药工程知识深度绑定:在提示中融入物化规律、USP规范等;
- 利用RAG检索功能,让LLM可访问外部数据库、文献;
- 加入RLHF,在实时实验反馈中修正模型参数,减少“幻觉”。
-
关键数据支持
- 各类溶出度测试中,LLM的预测曲线与真实数据比对,MSE最低达到10.55,R²最高可至0.99;
- Zero-shot, Few-shot, CoT等多种提示方式在论文中进行横向对比,实证其准确性与可靠性提升。
-
可能的反驳及应对
- 反驳:LLM预测是否过于“黑箱”?监管审评可能质疑模型可靠性。
应对:在提示中引入已公开的药典规则;结果接受专家审查并且可结合机理方程(Nernst-Brunner等)进行后续解释。 - 反驳:缺乏足够的训练数据怎么办?
应对:结合检索增强(RAG),不断调用新文献和数据库,减少对单一大规模标签数据的依赖。
- 反驳:LLM预测是否过于“黑箱”?监管审评可能质疑模型可靠性。
6. HOW GOOD —— 理论贡献与实践意义
-
理论贡献:
- 构建了一个将LLM与机理模型、实验数据库相结合的整体框架,为其他领域(如材料科学、食品工程)提供可借鉴思路;
- 提示工程与大语言模型的结合,为数据稀缺或多学科交叉的应用场景提供新的高效解决途径。
-
实践意义:
- 显著加快了药物开发流程:通过对溶出曲线的准确预测,研发人员可减少大量重复试验;
- 降低成本、提高成功率:逆向设计在满足监管要求的同时,缩短了从初步配方到临床前工艺放大的周期;
- 为个性化药物与精准用药奠定了技术基础:在未来,可进一步结合患者数据,设计个体化的固体制剂。
-
为什么要用 LLM(大型语言模型)来做溶出预测和逆向设计?
- 因为传统的物理模型(DEM/FEA)或传统机器学习需要大量的数据与计算,且难以在复杂多参数场景下做快速预测。
-
为什么传统方法缺少灵活性、需要大量标注数据?
- 因为纯物理仿真通常会简化系统、假设条件理想,而传统 ML 又严重依赖标注数据;现实中的药物溶出涉及多重参数(粒径分布、溶解度、扩散系数等),数据很分散、不易统一。
-
为什么多重参数会导致实验和仿真成本高昂?
- 制剂过程要考虑处方、工艺、设备、环境等交互因素;稍有变化就要重新做试验或仿真,这在药企或者学术研究中都极其耗时耗钱。
-
为什么LLM 能在缺乏完整大规模标注数据的情况下仍然有效?
- 一方面,LLM 在预训练过程中拥有海量文本知识(文献/专利等),可以通过 Prompt(提示)唤起相关理论与经验;另一方面,引入提示工程(Few-Shot、RAG 等)可以减少“幻觉”,将零星真实数据和文献检索信息整合起来。
-
为什么要把逆向设计(例如根据目标溶出率设计粒径)与 LLM 结合?
- 药物颗粒工程对逆向设计需求很高:想要满足不同患者或不同制剂规格时,需要迅速反推工艺参数。LLM 的自然语言理解和推理能力,可以帮助研究者快速筛选并生成可行方案,缩短研发周期。
解法拆解
本文核心目标:
利用大模型(DeepSeek LLM),结合提示工程(Prompt Engineering),对固体制剂(片剂/胶囊)的溶出行为进行预测和逆向设计,并结合实验/模拟结果进行验证。
1.1 主解法整体逻辑
主解法:
“DeepSeek LLM + Prompt Engineering + 评价指标(MSE、R²)+ 实验验证”
用于预测和设计溶出度曲线,进而给出颗粒物性(粒径分布、比表面积、溶解度等)的建议,或者根据目标溶出度反推粒径、溶解度、扩散系数等参数。
主要的技术框架与流程包括:
- Prompt Engineering:基于不同提示方式(零样本 Zero-Shot,少样本 Few-Shot,Chain-of-Thought,RAG 检索增强等),指导 LLM 输出溶出曲线或逆向设计的结果。
- 溶出模型理论基础:引用经典方程(Nernst-Brunner、径向扩散模型)以及相关文献(Salish et al.、Djukaj et al.)。
- 评价指标:采用真实或模拟的溶出数据,与 LLM 生成的溶出曲线进行对比,并用 MSE 与 R² 评估预测准确度。
- 实验/模拟数据验证:将 LLM 的输出与实验所得溶出度曲线(如使用 USP II 桨法测定)进行对比验证。
- 决策或应用:若模型预测较准,可用于工艺设计、粉体工程、配方流程中;若不准,则可通过加强提示或结合更多外部数据库(RAG)进一步优化。
与传统/同类算法(例如纯物理仿真或传统机器学习)相比,本文方法的主要区别在于:
- 无需大量标注数据:LLM 可以通过提示(prompts)从已有文献知识和少量样本中学习溶出机理与参数影响关系,而传统 ML 往往需要大规模标注数据集。
- 可实现灵活的逆向设计:通过自然语言提示,让模型直接给出“若想在 1 小时内达到 85% 溶出,需要怎样的粒径分布”,从而更轻量地将工艺设计与机理模型结合。
- 可动态检索和多步推理:RAG、CoT 等提示方式让 LLM 能够先检索/回顾文献原理,再多步骤推理,不仅仅是单一的输入输出映射。
1.2 进一步拆解「主解法」为子解法
从文中来看,整个解法核心地分成 5 个子解法,分别是基于提示策略的五种主要“运用模式”:
-
子解法1:零样本(Zero-Shot, ZS)
- 之所以用 ZS 子解法,是因为:当没有任何示例时,模型依赖大规模预训练知识库,以及提示中明确的背景和要求(如溶解度、扩散系数等),直接推断溶出结果。
- 在无示例情况下依旧有较好表现,但也可能出现推理不充分或幻觉(hallucination)的风险。
-
子解法2:零样本 + Chain-of-Thought (ZS CoT)
- 之所以用 ZS CoT 子解法,是因为:希望在无示例的情况下,通过显式要求模型“分步骤思考”,来提高其推理的透明度和准确度。
- 但文中实验发现,ZS CoT 反而精度下降,说明如果没有足够的上下文支持,显式让模型“自我分解”可能出现逻辑链断裂或“编造”中间结论的情况。
-
子解法3:少样本(Few-Shot, FS)
- 之所以用 FS 子解法,是因为:通过提供 1~3 个具有相似输入输出格式的示例,让模型学习如何“输出溶出度时间序列”,并期望比零样本更贴近真实情况。
- 但如果示例较少或不够通用,可能会引入噪声。
-
子解法4:少样本 + Chain-of-Thought (FS CoT)
- 之所以用 FS CoT 子解法,是因为:在给了少量示例的基础上,再让模型显式地按步骤推理,可以在案例指导下实现更稳定的多步推理。
- 文中结果显示该模式明显优于单纯少样本,有接近 Zero-Shot 的优秀拟合度,并显著降低 MSE。
-
子解法5:检索增强生成(RAG)
- 之所以用 RAG 子解法,是因为:引入外部数据库或文献(如 FDA 溶出数据库、文献资料),可以让模型在回答前检索到与当前药物、实验条件更相似的真实数据,进而减少臆测。
- 结果显示 RAG 模式在文中达到了最佳预测准确度(MSE 最低、R² 最高)。
综上,主解法 = 子解法1(ZS) + 子解法2(ZS CoT) + 子解法3(FS) + 子解法4(FS CoT) + 子解法5(RAG)。
1.3 每个子解法与“溶出模型”的对应关系
文中多次提到 Nernst-Brunner、径向扩散等方程。大体上,这些方程为溶出过程提供了物理基础(溶质传质、扩散系数、比表面积等)。LLM 在不同提示模式下,都可能内嵌或“记忆”了这类方程,或者通过检索外部文献而得到,因此有时候在回答中会在引用或基于这些物理模型对粒子大小、时间、溶出百分比进行推断。
- 隐含解法:LLM 并不是自己从头推导方程,而是(1)要么在预训练语料中已有(2)要么在 RAG 检索到并复用。
- 区别:相比传统显式数值模拟(DEM/FEA)或经典 ODE/PDE 求解,这里是让一个通用的语言模型在自然语言层面进行概化推理,背后依旧依托公式(或文字化的公式),但计算方式更像是“模式识别+语言生成”的过程。
2. 这些子解法是什么样的逻辑链?(以决策树形式列出)
可以将上面 5 种子解法看成一个“如何提示 LLM 进行溶出预测/设计”的决策树。简单表示如下:
┌─── 子解法1: Zero-Shot (ZS)
│ (无示例, 直接给模型背景信息与需求)
┌───────► (A) 基础提示
│ └─── 子解法2: Zero-Shot + CoT (ZS CoT)
│ (要求模型“先写推理过程,再给结论”)
提示工程策略 ──┤
│ ┌─── 子解法3: Few-Shot (FS)
│ │ (提供1~3个示例, 再让模型输出结果)
└───────► (B) 少量示例
└─── 子解法4: Few-Shot + CoT (FS CoT)
(少量示例 + 多步推理)
(可选增强) ─────────────────────► 子解法5: RAG
(引入外部数据库/文献, 减少幻觉/不确定)
从决策树可以看到,如果不提供示例,就走 (A) 路线;如果提供少量示例,就走 (B) 路线;在任何路线中,还可选择是否加 CoT;此外,还能额外叠加 RAG(检索增强)来减少错误和不确定性。
3. 分析是否有隐性方法
隐性方法指不在教科书或文献中直接命名,但在本研究方案里起关键作用的步骤/策略。本文潜在的“隐性方法”主要有:
-
显式的“多步推理模板化提示”:
- 传统文献不会专门介绍“如何写 Prompt 来让模型先列出 Nernst-Brunner 公式、再进行溶出计算”,但在文中作者设计了一个 JSON 格式的 Structured Prompt,要求模型输出特定表格、根据 USP 标准输出释放度等。这是一种关键方法,但在传统粒子工程/药剂学书本中并不存在对应章节。
- 可以将其定义为:“Prompt 模板构造 + 结构化输出 + 强制多步分析”的关键方法。
-
少样本 + Chain-of-Thought 联合示例:
- 单纯少样本或单纯 CoT 在其它文本中也许被提及,但将二者结合并针对药物溶出这个具体场景专门写例子(Example1/Example2/Example3),再令模型依照此推理格式产出更高精度的溶出数据,这在一般的 ML/AI 教材中没有现成范式。
- 这也可以视为一个隐藏的中间步骤:通过示例“诱导”模型的推理链自动对齐到正确的溶出机理。
-
RAG 的外部数据库整合:
- 典型教材会讲到检索文献数据,但不会详细讨论“如何在线调用 FDA 溶出数据库并实时与 LLM 交互”。文中把 RAG 作为实现低 MSE、高 R² 的关键措施,这也是隐性方法之一。
因此,可以归纳为一个关键方法:“Prompt 工程 +(可选)外部数据检索” 的多步集成策略,是本研究在传统药物溶出/粒子设计流程之上额外新增的解决方案。
4. 分析是否有隐性特征
隐性特征指在解法过程中使用了但未在“问题或基本条件”明确列出的中间变量/特征,或者是通过多步推理才出现的推导需求。根据文中描述,可能的隐性特征有:
-
粒子间相互作用系数、混合工艺因子:
- 文中多次提到“流动性”或“机械力学特性”是后续研究方向,但现在的模型只关注粒径/形状/溶解度/扩散系数等,隐藏了对真实生产中混合效率、粘结力等特征的考虑。
- 这说明在实际工艺中会出现的“黏附力、团聚行为”等特征,没有在本文提示工程里显式输入,属于潜在影响因素。
-
溶出介质(pH、表面活性剂)的动态变化:
- 在文中,虽然实验采用 pH 7.2 或 pH 6.2 的缓冲液,但在 LLM 的推理提示中,往往只给出一个固定 pH 或仅简单说明“符合 USP 标准”。在真实情境下,介质可能随时间/溶出过程发生 pH 浮动或表面张力变化,这些都可能是隐性特征。
- 目前在提示工程中未必显式包含介质属性的动态变化,只是以恒定值处理。
这些隐性特征若要显式纳入模型,需要在 Prompt 或数据检索阶段做更多工作。目前它们并未构成文中直接显示的输入条件,但可能在模型内部隐式处理或造成预测偏差。
5. 方法可能存在哪些潜在的局限性
-
数据依赖与漂移
- LLM 的预训练语料与外部检索文献是否包含足够多的同类型药物/制剂数据?若检索不足或语料本身偏离目标药物属性,可能导致输出错误或“幻觉”。
- 如果目标药物或新分子实体(NME)与文献已有案例差异很大,模型预测的可靠性将降低。
-
解释性与监管合规
- 药品开发领域高度监管,需要对各项参数和计算过程做详细审计。LLM 的推理过程往往是“黑箱”式的,哪怕有 CoT 也不一定能在监管层面完全透明。
- 逆向设计得到的粒径/溶解度等建议,仍需要实验验证才能获得监管批准。
-
少量示例与过拟合/偏置
- 在 Few-Shot、Few-Shot CoT 场景,如果示例选择不当,会引入明显偏差。
- 如果示例数据本身质量不好或不具有代表性,模型可能将错误信息“放大”。
-
大模型通用性与计算成本
- DeepSeek 这种 671B 级别参数的模型体量极大,推理开销(显存/时间)高,对实验室或企业的硬件配置有要求。
- 若要大规模在线推断或实时逆向设计,如何控制成本并保持响应速度,也是实际应用时的挑战。
-
隐性特征未纳入
- 正如上文提到的混合工艺参数、流动性、机械性能乃至辅料相容性等,都尚未整合进当前提示工程,可能导致在工业实际中出现额外风险和预测偏差。
提示词
# 角色: ##
你好,你是一位药物开发专家。
你可以设计自定义的溶出度动力学或根据给定的物理特性(如粒度分布等)预测药物释放度(%)。
## 背景: ##
你对这一领域拥有丰富经验,并且
曾经研究过常用的经验扩散模型,比如 Nernst-Brunner 翻译溶出和径向扩散动力学,参考:
(1) Salish, K., So, C., Jeong, S. H., Hou, H. H., Mao, C. “A Refined Thin-Film Model for Drug Dissolution Considering Radial Diffusion — Simulating Powder Dissolution.” Pharm Res 41, 947-958 (2024).
(2) Djukaj, S., Kolar, J., Lehocky, R., Zadrazil, A., Stepanek, F. “Design of particle size distribution for custom dissolution profiles by solving the inverse problem.” Powder Technology: An International Journal on the Science and Technology of Wet and Dry Particulate Systems, 395 (2022).
# 请求: #
1. 客户会给你若干基础参数;基于这些参数,
2. 你需要为客户预测药物释放度(%),或者
3. 根据给定的溶出度曲线(溶出速率)来设计药物的物理性质并优化条件。
# 输入格式: #
Input = {
"Mean Particle Size, D50": 97.5,
"Aspect ratio": 1.0,
"Roundness": 1.0,
"solubility of drug (mg/mL)": 0.45,
"Diffusion coefficient of drug (m^2/s)": 7.5 x 10^(-10),
"True Density of drug (g/mL)": 1.512,
"Specific surface area (m^2/g)": 1.07,
"volume-based equivalent particle size (micrometer)": 1.85
}
# 输出格式: ##
请生成一个包含以下列的表格: [Time(min), Drug Released(%)]。
包括关键时间点: (t_(0), t_(0.25), t_(0.5), t_(0.75), t_(1), t_(2), t_(3), t_(4), t_(5), t_(6))
其中 t 代表“Time(hrs)”的缩写。
"columns": ["Time (hr)", "Drug Released (%)"]
"data": [
[0, 0],
[0.25, 85],
[0.5, 87],
[0.75, 88],
[1, 89],
[2, 89],
[3, 89],
[4, 88],
[5, 87],
[6, 87]
]
# 示例: ##
无示例提供
# 约束条件: #
1. Nernst-Brunner 方程 = {
V * (dx_H / dt) = (k * ψ_i * A_H^3 / ρ_s * ψ_v) * [ C_fi(text(sat)) - C_b ]
其中 Vk = (Sh * (D_H * x))。
且 Sh = 2 + 0.52 * (Re^(0.52)) * (Sc^(1/3)).
}
2. 在 60 分钟内最终溶出度 ≥ 85%(符合 USP 要求)。
3. 请不要无根据地提出建议。
4. 只提供有清晰科学依据的优化方法。
5. 如果你可能无法提供正确答案,请不要随意编造。
--------------------
## Few-shot 示例: ###
# Example1: ###
Input = {
"Mean Particle Size, D50": 45,
"Aspect ratio": 1.0,
"solubility of drug (mg/mL)": 0.45,
"Diffusion coefficient of drug (m^2/s)": 7.5 x 10^(-10),
"True Density of drug (g/mL)": 1.512,
"Specific surface area (m^2/g)": 1.70,
"volume-based equivalent particle size (micrometer)": 1.17
}
# 输出: ###
"columns": ["Time (hr)", "Drug Released (%)"],
"data": [
[0, 0],
[0.25, 85],
[0.5, 87],
[0.75, 88],
[1, 89],
[2, 89],
[3, 89],
[4, 88],
[5, 87],
[6, 87]
]
--------------------
# Example2: ###
Input = {
"Mean Particle Size, D50": 200,
"Aspect ratio": 1.0,
"Roundness": 1.0,
"solubility of drug (mg/mL)": 0.45,
"Diffusion coefficient of drug (m^2/s)": 7.5 x 10^(-10),
"True Density of drug (g/mL)": 1.512,
"Specific surface area (m^2/g)": 0.24,
"volume-based equivalent particle size (micrometer)": 8.14
}
# 输出: ###
"columns": ["Time (hr)", "Drug Released (%)"],
"data": [
[0, 0],
[0.25, 12],
[0.5, 20],
[0.75, 28],
[1, 35],
[2, 52],
[3, 63],
[4, 71],
[5, 75],
[6, 82]
]
--------------------
# Example3: ###
Input = {
"Mean Particle Size, D50": 97.5,
"Aspect ratio": 1.0,
"Roundness": 1.0,
"solubility of drug (mg/mL)": 0.45,
"Diffusion coefficient of drug (m^2/s)": 7.5 x 10^(-10),
"Specific surface area (m^2/g)": 0.16,
"volume-based equivalent particle size (micrometer)": 11.94
}
# 输出: ###
"columns": ["Time (hr)", "Drug Released (%)"],
"data": [
[0, 0],
[0.25, 32],
[0.5, 40],
[0.75, 56],
[1, 60],
[2, 72],
[3, 76],
[4, 80],
[5, 82]
]